条件概率和全概率公式

条件概率公式

1.条件概率公式:设A,B为两个事件，且P(B)>0，则称为事件B已经发生的条件下事件A发生的条件概率，记为P(A|B),即：

                                             =   

---

2.乘法定理：由条件概率定义   ，两边同乘以P(A)可得P(AB)=P(A)P(B|A),由此可得定理：

                                                设P(B)>0,则有P(AB)=P(A)P(B|A)

乘法定理推广：设A，B，C为3个事件，P(AB)>0；则有：                          P(ABC)=P(C|AB)P(AB)=P(C|AB)P(B|A)P(A)

---

全概率公式

全概率公式：设B为样本空间中的任一事件，A1,A2.....An为的一个划分，且P(Ai)>0,i=1,2,3.....n，则有P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+....+P(An)P(B|An)=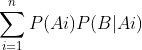,称该公式为全概率公式

---

贝叶斯公式                

贝叶斯方式：设样本空间为，B为样本空间的事件，A1,A2....An为样本空间的一个划分，且P(B)>0,P(Ai)>0,i=1,2,3...n,则有：,i=1,2....n,c称为贝叶斯公式，也称为逆概率公式

---

独立性

定义：若事件A1,A2满足：P(A1A2)=P(A1)P(A2)，则称事件A,B相互独立

定理：若事件A与B相互独立，则下列各事件也相互独立：

定理：若事件A,B相互独立，且0)=P(B)

定义:设A1,B2,C3是3个事件。如果同时满足：

P(A1B2)=P(A1)P(B2),

P(A1C3)=P(A1)P(C3),

P(B2C3)=P(B2)P(C3),

P(A1B2C3)=P(A1)P(B2)P(C3)

则称A1,B2,C3为相互独立事件

定义：P(A1A2....An)=P(A1)P(A2)...P(An),则称A1,A2...An是相互独立事件

·若A1,A2...An事件相互独立，则其中任意k个事件也相互独立

·若A1,A2...An事件相互独立，则其中任意个事件的对立事件也相互独立

---

伯努利实验

若实验E只有A和,则称E为伯努利实验，设P(A)=p，0=1-p；将E实验重复进行n次，则这一连串重复试验为n重伯努利实验

n重伯努利实验中A出现k次的概率计算公式：, k=0,1,2...n