泊松融合进阶——DFT求解二维泊松方程

前言

泊松融合（Poisson Blending）是图像处理领域著名的图像融合算法，自从2003年发表以来，有很多基于此算法的应用和改进研究出现。泊松融合无需像Alpha blending一样的精确抠图就可以得到很自然的结果。

关于泊松融合原理部分的解析见之前的博客《泊松融合原理浅析》。

关于针对OpenCV中泊松融合的实现代码（以normalClone为例）进行解读的部分见之前的博客《OpenCV源码解读：泊松融合seamlessClone（normalClone）》。

在上文中有提到，OpenCV的整个泊松融合算法过程是基于离散傅里叶变换求解泊松方程实现的。在本文，将针对这一方法进行深入分析。

基础知识

先复习一下梯度、拉普拉斯、散度的基本知识，然后简要说明泊松融合和泊松方程的关系。

梯度，拉普拉斯，散度

其中，$\mu =\frac{\partial f}{\partial x}$，$\nu =\frac{\partial f}{\partial y}$。另外需要说明的一点是二维图像的散度全称应该是梯度的散度，也就是拉普拉斯。

对于二维图形而言，梯度有两个方向（x和y）：
在OpenCV源码中，计算梯度的部分如下：

//求X方向的梯度
void Cloning::computeGradientX( const Mat &img, Mat &gx)
{
    //X方向梯度核
    Mat kernel = Mat::zeros(1, 3, CV_8S);
    kernel.at<char>(0,2) = 1;
    kernel.at<char>(0,1) = -1;

    if(img.channels() == 3)
    {
        filter2D(img, gx, CV_32F, kernel);
    }
    else if (img.channels() == 1)
    {
        filter2D(img, gx, CV_32F, kernel);
        cvtColor(gx, gx, COLOR_GRAY2BGR);
    }
}

//求Y方向的梯度
void Cloning::computeGradientY( const Mat &img, Mat &gy)
{
    //Y方向梯度核
    Mat kernel = Mat::zeros(3, 1, CV_8S);
    kernel.at<char>(2,0) = 1;
    kernel.at<char>(1,0) = -1;

    if(img.channels() == 3)
    {
        filter2D(img, gy, CV_32F, kernel);
    }
    else if (img.channels() == 1)
    {
        filter2D(img, gy, CV_32F, kernel);
        cvtColor(gy, gy, COLOR_GRAY2BGR);
    }
}

拉普拉斯是在梯度的基础上得到的，可以看做是X方向和Y方向的二阶梯度和。

在OpenCV源码中，计算拉普拉斯的部分是在梯度图的基础上进行的：

//求X方向的拉普拉斯
void Cloning::computeLaplacianX( const Mat &img, Mat &laplacianX)
{
    Mat kernel = Mat::zeros(1, 3, CV_8S);
    kernel.at<char>(0,0) = -1;
    kernel.at<char>(0,1) = 1;
    filter2D(img, laplacianX, CV_32F, kernel);
}

//求Y方向的拉普拉斯
void Cloning::computeLaplacianY( const Mat &img, Mat &laplacianY)
{
    Mat kernel = Mat::zeros(3, 1, CV_8S);
    kernel.at<char>(0,0) = -1;
    kernel.at<char>(1,0) = 1;
    filter2D(img, laplacianY, CV_32F, kernel);
}

Mat lap = laplacianX + laplacianY;//得到梯度的散度（也就是拉普拉斯）

泊松融合与泊松方程

泊松融合的核心思想不是让需要融合的两张图像直接叠加，而是让目标图像（dst）在融合部分根据源图像（src）的引导场（实际是梯度场 gradient field ）“生长”出新的图像。

也就是说，只需要提供源图像的梯度场，让目标图像根据自身特点，按照源图像对应的梯度场生成融合部分。由于目标图像是按照自身特点出发生成融合区域，所以融合结果会显得更加自然。

在上述示意图中，$S$是二维实数集${\mathbb{R}}^2$的闭合子集，$\Omega$是$S$的边界为$\partial \Omega$闭合子集。$f^{\ast }$是集合 $S-\Omega$ 部分的函数（如果是图像的话就是指所有像素的像素值），$f$是集合 $\Omega$ 的函数（也就是需要靠解泊松方程来求的函数）。$\mathbf{v}$是集合$\Omega$的向量场（构建泊松方程所需）。

插值结果是如下最小化问题的解：

该问题的解是如下带有狄利克雷边界条件的泊松方程，由此建立起泊松融合与泊松方程之间的关系。

注：狄利克雷（Dirichlet）边界条件是指给定函数值本身在边界条件上的值，而诺伊曼（Neumann）边界条件是指给定函数的一阶梯度在边界条件上的值。

对于二维图像而言，像素点是离散点，因此上述连续空间的偏微分方程可以改写为离散空间的偏微分方程：

其中，p是S中的像素点，$N_p$是像素p的四邻域，是像素对。此时$\Omega$的边界变为$\partial \Omega =\{p\in S\setminus \Omega :N_p\cap \Omega \ne \varnothing \}$。$f_p$是$f$在p点的值。

等式(6)的解满足如下联立线性方程：

当方程中的像素p的四邻域不包含边界点（$\partial \Omega$）时：

关于泊松方程的求解，方程(7)形式构成一个经典的、稀疏带状、对称、正定系统。可以通过带successive overrelaxation（逐次超松弛）的Gauss-Seidel iteration（高斯-赛德尔迭代）或者V-cycle multigrid方法求解。

根据泊松方程构建形式的不同可以选择上述两种不同的方法进行求解。

可以看到，上述中的边界通常是不规则的，不便于求解。对于实际图像融合需求来说，我们可以通过在可控条件下扩展融合边界，以此来构建更易求解的方程形式，并加速整个泊松方程的求解过程。

这就是采用离散傅里叶变换求解泊松方程的出发点。

DFT解2D泊松方程

思想介绍

在上图中，给出了任意形式的边界条件$\partial \Omega$。而实际上，我们可以将该边界松弛成一个矩形框roi（例如$\partial \Omega$的外接矩形），此时边界条件可以看成是该矩形框，而内部的梯度则是$\Omega$区域的src梯度和 $roi-\Omega$ 区域的dst梯度的合集。

在OpenCV中，该部分的代码如下：

Mat laplacianX = destinationGradientX + patchGradientX;//将mask区域的源图像X方向梯度和非mask区域的模板图像X方向梯度叠起来，形成新的X方向梯度。此时laplacianX还不是拉普拉斯值
Mat laplacianY = destinationGradientY + patchGradientY;//将mask区域的源图像Y方向梯度和非mask区域的模板图像Y方向梯度叠起来，形成新的Y方向梯度。此时laplacianY还不是拉普拉斯值

computeLaplacianX(laplacianX,laplacianX);//计算X方向的拉普拉斯值
computeLaplacianY(laplacianY,laplacianY);//计算Y方向的拉普拉斯值

原先的狄利克雷边界条件也因此需要改动，在OpenCV实现中是构建了外接矩形处的诺伊曼（Neumann）边界条件。

Mat lap = laplacianX + laplacianY;//得到散度

Mat bound = img.clone();

rectangle(bound, Point(1, 1), Point(img.cols-2, img.rows-2), Scalar::all(0), -1);
Mat boundary_points;
Laplacian(bound, boundary_points, CV_32F);//得到边界像素的拉普拉斯。注：对一个标量场求梯度后再求散度，等于拉普拉斯算子作用在其上。

boundary_points = lap - boundary_points;//散度差，构建诺伊曼边界条件

在构建好带诺伊曼边界条件的泊松方程后，采用谱变换方法——离散傅里叶变换求解方程，OpenCV中是采用了离散正弦变换dst求解（源码中有构建奇对称图像的部分，DST求解的整体长度变为原始DFT的2倍左右）。

注：离散正弦变换（DST for Discrete Sine Transform）是一种与傅立叶变换相关的变换，类似离散傅立叶变换，但是只用实数矩阵。离散正弦变换相当于长度约为它两倍，一个实数且奇对称输入资料的的离散傅立叶变换的虚数部分（因为一个实奇输入的傅立叶变换为纯虚数奇对称输出）。有些变型里将输入或输出移动半个取样。
一种相关的变换是离散余弦变换，相当于长度约为它两倍，实偶函数的离散傅立叶变换。

注意上述代码中的：

Mat temp = Mat::zeros(src.rows, 2 * src.cols + 2, CV_32F);//注意2倍关系，求解dst需要构建对称关系

构建出的新的用于求解的序列长度为2*L+2，像素值关系示意如下（假设原始L=3），整体按行呈现出奇对称关系。

另外，2D FFT可以通过两个1D FFT实现（先行变换再列变换或者反之）。需要注意存储矩阵的变换以及新的奇对称关系构建。

公式推导

连续域的2D 泊松方程形式如下：

而对于图像而言，是离散域，转为有限差分方程表示：

函数u(x, y)可以表示为：

于是可以得到：

注：${\Delta }^2$是二阶差分，即一阶差分$\Delta$的差分。

我们的目标是求解${\mu }_{j,l}$。

首先，记以下缩写，后续推导会用到：

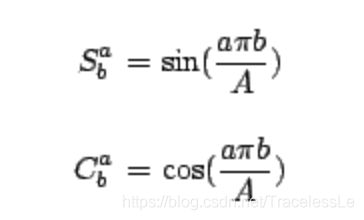
以及2D discrete cosine transform的逆变换：

代入有限差分方程（时域方程）两侧并消除求和符号，得到频域方程：

又有：

所以：

又：

为了求解${\hat{\mu }}_{m,n}$，简化方程形式：

因此：

代入最初的缩写，得到：

根据上述推导，求解泊松方程，总体分为三大步骤：

1. 先求2D DST得到${\hat{\rho }}_{m,n}$
2. 再除以分母$2(cos(\frac{\pi m}{J})+cos(\frac{\pi n}{L})-2)$
3. 最后再通过逆2D DST重建出${\mu }_{j,l}$。

注：其中2D DST可以通过构建两个1D DFT实现（先行变换再列变换或者反之）。
The 2-D FFT block computes the fast Fourier transform (FFT). The block does the computation of a two-dimensional M-by-N input matrix in two steps. First it computes the one-dimensional FFT along one dimension (row or column). Then it computes the FFT of the output of the first step along the other dimension (column or row).

OpenCV该部分的实现代码如下：

dst(mod_diff, res);//对传入的散度差调用dst方法求解

for(int j = 0 ; j < h-2; j++)
{
    float * resLinePtr = res.ptr<float>(j);
    for(int i = 0 ; i < w-2; i++)
    {
        resLinePtr[i] /= (filter_X[i] + filter_Y[j] - 4);
    }
}//调整dst过程参数的系数

dst(res, mod_diff, true);//对第一次dst得到的结果调整后调用逆dst方法求解

至此，泊松方程求解完成，整个泊松融合的核心过程结束。

版权说明

本文为原创文章，独家发布在blog.csdn.net/TracelessLe。未经个人允许不得转载。如需帮助请email至[email protected]。

参考资料

[1] 泊松融合原理浅析
[2] OpenCV源码解读：泊松融合seamlessClone（normalClone）
[3] 拉普拉斯算子 - 维基百科，自由的百科全书
[4] 狄利克雷边界条件 - 维基百科，自由的百科全书
[5] 诺伊曼边界条件 - 维基百科，自由的百科全书
[6] 关于使用dct求解零诺依曼边界条件PDE的一点说明
[7] 使用傅里叶变换（包括差分傅里叶和傅里叶谱方法）及切比雪夫谱方法（配点）法求解PDE
[8] void Cloning::dst(const Mat& src, Mat& dest, bool invert)
[9] 离散正弦变换 - 维基百科，自由的百科全书
[10] Solving a 2D Poisson equation with Neumann boundary conditions through discrete Fourier cosine transform
[11] NUMERICAL RECIPIES IN C, 2ND EDITION (by PRESS, TEUKOLSKY, VETTERLING & FLANNERY) —— Chapter 19. Partial Differential Equations —— P851
[12] 差分- 维基百科，自由的百科全书
[13] OpenCV泊松融合实现源码——opencv/modules/photo/src/seamless_cloning_impl.cpp
[14] cupoisson/poisson.cu
[15] 傅里叶正弦、余弦变换 - 维基百科，自由的百科全书
[16] 泊松图像编辑/融合（Possion image editing）的原理与数值解算法
[17] Fast algorithm for Poisson equation
[18] Poisson Image Editing Theory and Fourier Approach
[19] Fast Poisson Equation Solver using DCT
[20] 二维离散傅里叶（DFT）与快速傅里叶（FFT）的实现
[21] 2-D FFT - Compute two-dimensional fast Fourier transform of input
[22] Accelerating a barotropic ocean model using a GPU
[23] 二维傅里叶变换是怎么进行的？