SuperPoint 与 SuperGlue 详解(一)
1. 简介
SuperPoint: Self-Supervised Interest Point Detection and Description (CVPR 2018)
论文地址
代码地址
SuperGlue: Learning Feature Matching with Graph Neural Networks (CVPR 2020)
论文地址
代码地址
两篇论文都出自 Magic Leap 团队,SuperPoint 提取特征点及描述符,SuperGlue 做特征点匹配
2. SuperPoint
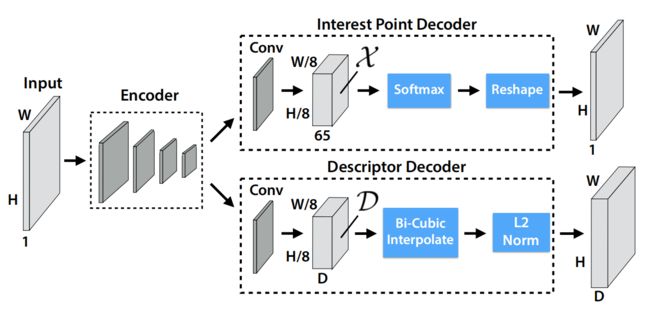
2.1 网络结构
网络结构如上图所示,基本就是特征提取网络加两个分支,一个分支输出特征点的位置和得分(置信度),另一个分支输出特征点的描述符。网络中的计算操作都比较常规,检测分支里的第65个通道代表无特征点,NMS的具体细节见 SuperPoint 特征点 NMS 代码分析。
2.2 训练总流程
SuperPoint 的网络结构并不复杂,而难点在于如何训练网络,尤其是如何得到训练数据,如何在自然图像上标注特征点(论文中说,与人体关键点检测等任务相比,无法清晰地定义特征点检测的概念;个人理解就是即使用人为标注,也没法得到一个基本统一的 ground truth)。
论文中给出了自监督的解决方案,具体流程如下:

(a)用简单的几何形状(特征点坐标明确)创建一个名为 Synthetic Shapes 的合成数据集,来训练一个全卷积网络作为 Base Detector。文中把这个训练好的检测器称为 MagicPoint,MagicPoint 在 Synthetic Shapes 数据集上明显优于传统算法,在真实图像上表现也很好,但是会漏掉一些潜在的特征点。
(b)为了弥补在真实图像上的性能差距,开发了 Homographic Adaptation 技术,实现检测器的自监督训练,提升 MagicPoint 的性能,并在自然图像上生成伪 ground truth 。
(c)事实上在b阶段完成后,已经得到了 SuperPoint 的特征点检测部分,之后就是通过对图像做变换得到特征点的对应关系作为 ground-truth 来训练 SuperPoint 的描述符部分。
2.3 SuperPoint 损失函数
L ( X , X ′ , D , D ′ ; Y , Y ′ , S ) = L p ( X , Y ) + L p ( X ′ , Y ′ ) + λ L d ( D , D ′ , S ) \mathcal{L}\left(\mathcal{X}, \mathcal{X}^{\prime}, \mathcal{D}, \mathcal{D}^{\prime} ; Y, Y^{\prime}, S\right)=\mathcal{L}_{p}(\mathcal{X}, Y)+\mathcal{L}_{p}\left(\mathcal{X}^{\prime}, Y^{\prime}\right)+\lambda \mathcal{L}_{d}\left(\mathcal{D}, \mathcal{D}^{\prime}, S\right) L(X,X′,D,D′;Y,Y′,S)=Lp(X,Y)+Lp(X′,Y′)+λLd(D,D′,S)
整个 l o s s loss loss 由两部分组成, L p \mathcal{L}_{p} Lp 计算特征点位置损失, L d \mathcal{L}_{d} Ld 计算特征点描述符损失。
L p ( X , Y ) = 1 H c W c ∑ h = 1 w = 1 H c , W c l p ( x h w ; y h w ) \mathcal{L}_{p}(\mathcal{X}, Y)=\frac{1}{H_{c} W_{c}} \sum\limits_{h=1 \atop w=1}^{H_{c}, W_{c}} l_{p}\left(\mathbf{x}_{h w} ; y_{h w}\right) Lp(X,Y)=HcWc1w=1h=1∑Hc,Wclp(xhw;yhw)
l p ( x h w ; y ) = − log ( exp ( x h w y ) ∑ k = 1 65 exp ( x h w k ) ) l_{p}\left(\mathbf{x}_{h w} ; y\right)=-\log \left(\frac{\exp \left(\mathbf{x}_{h w y}\right)}{\sum_{k=1}^{65} \exp \left(\mathbf{x}_{h w k}\right)}\right) lp(xhw;y)=−log(∑k=165exp(xhwk)exp(xhwy))
输入图像大小为 H , W H,W H,W,公式中 H c = H / 8 , W c = W / 8 H_{c}=H/8,W_{c}=W/8 Hc=H/8,Wc=W/8,而 L p \mathcal{L}_{p} Lp 就是计算一个交叉熵损失。论文中有个细节,在一个 h w hw hw 的区域里面如果存在多个特征点,会随机取一个作为 ground-truth。这样每个区域就是做个65类分类问题。
L d ( D , D ′ , S ) = 1 ( H c W c ) 2 ∑ h = 1 w = 1 H c , W c ∑ h ′ = 1 w ′ = 1 H c , W c l d ( d h w , d h ′ w ′ ′ ; s h w h ′ w ′ ) \mathcal{L}_{d}\left(\mathcal{D}, \mathcal{D}^{\prime}, S\right)=\frac{1}{\left(H_{c} W_{c}\right)^{2}} \sum\limits_{h=1 \atop w=1}^{H_{c}, W_{c}} \sum\limits_{h^{\prime}=1 \atop w^{\prime}=1}^{H_{c}, W_{c}} l_{d}\left(\mathbf{d}_{h w}, \mathbf{d}_{h^{\prime} w^{\prime}}^{\prime} ; s_{h w h^{\prime} w^{\prime}}\right) Ld(D,D′,S)=(HcWc)21w=1h=1∑Hc,Wcw′=1h′=1∑Hc,Wcld(dhw,dh′w′′;shwh′w′)
l d ( d , d ′ ; s ) = λ d ∗ s ∗ max ( 0 , m p − d T d ′ ) + ( 1 − s ) ∗ max ( 0 , d T d ′ − m n ) l_{d}\left(\mathbf{d}, \mathbf{d}^{\prime} ; s\right) =\lambda_{d} * s * \max \left(0, m_{p}-\mathbf{d}^{T} \mathbf{d}^{\prime}\right)+(1-s) * \max \left(0, \mathbf{d}^{T} \mathbf{d}^{\prime}-m_{n}\right) ld(d,d′;s)=λd∗s∗max(0,mp−dTd′)+(1−s)∗max(0,dTd′−mn)
s h w h ′ w ′ = { 1 , if ∥ H p h w ^ − p h ′ w ′ ∥ ≤ 8 0 , otherwise s_{h w h^{\prime} w^{\prime}}=\left\{\begin{array}{ll} 1, & \text { if }\left\|\widehat{\mathcal{H} \mathbf{p}_{h w}}-\mathbf{p}_{h^{\prime} w^{\prime}}\right\| \leq 8 \\ 0, & \text { otherwise } \end{array}\right. shwh′w′={1,0, if ∥∥∥Hphw −ph′w′∥∥∥≤8 otherwise
出于计算量的考虑,描述符的损失在低分辨率 H c , W c H_{c},W_{c} Hc,Wc 上计算。 p h w \mathbf{p}_{h w} phw 为对应区域的中心点坐标, H p h w ^ \widehat{\mathcal{H} \mathbf{p}_{h w}} Hphw 是对 p h w \mathbf{p}_{h w} phw 做单应性变换 H \mathcal{H} H, s h w h ′ w ′ s_{h w h^{\prime} w^{\prime}} shwh′w′ 代表两个区域是否匹配。 L d \mathcal{L}_{d} Ld 就是计算一个 hinge loss,正边界 positive margin 取 m p m_{p} mp,负边界 negative margin 取 m n m_{n} mn;因为正负样本不平衡,用 λ d \lambda_{d} λd 平衡一下。
论文参数: λ d = 250 , m p = 1 , m n = 0.2 , λ = 0.0001 \lambda_{d}=250,m_{p}=1,m_{n}=0.2,\lambda=0.0001 λd=250,mp=1,mn=0.2,λ=0.0001
2.4 MagicPoint
(1)合成数据集 Synthetic Shapes

利用简单的几何形状创建合成数据集,合成图像在训练输入时会做动态随机单应性变换,网络不会输入重复图像(一般来说训练网络每个 epoch 的数据集是一样的,这里论文的意思应该是每个epoch的数据都是不同的,论文前面也说 Synthetic Shapes 有数百万个图像,后面说训练 MagicPoint 迭代了20w次)。虽然合成数据集中的特征点只是现实世界所有潜在特征点的一个子集,但是用来训练特征检测器时实践效果很好。
MagicPoint 的网络结构就是 SuperPoint 去掉描述符的分支。MagicPoint 在合成数据集上表现很好,在推广到真实图像时表现也很好,特别是在有角状结构的场景上(桌子、椅子、窗户)。但是视角变化时同一位置的特征点容易检测不到(Unfortunately in the space of all natural images, it underperforms when compared to the same classical detectors on repeatability under viewpoint changes.)。因此提出了在真实图像上的自监督训练方法 Homographic Adaptation。
(2)Homographic Adaptation
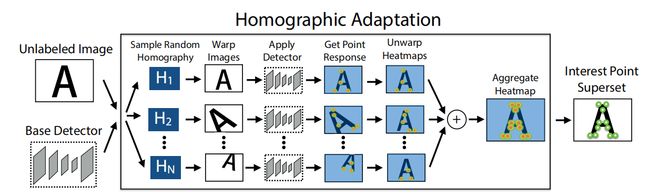
基本流程是对图像(此数据集为 MSCOCO2014 训练集分割生成 8w 个 240 × 320 240\times320 240×320 的灰度图像,这个数据集也用来训练 SuperPoint,单应性变换的选择比这里更严格)做多个随机单应性变换检测特征点,然后把所有的特征点结合作为标签。单应性变换也不是随便一个都行,要比较像相机从不同视角拍摄,如下图由多个简单的单应性变换组合而成。随机单应性变换的总数量 N h N_h Nh 通过实验取100性价比最高。

通过反复使用 Homographic Adaptation 迭代优化 MagicPoint,在 HPatches 上的性能提升效果如下图所示。

2.5 残留细节问题
官方不提供 SuperPoint 的训练和评估代码,以及合成数据集 Synthetic Shapes,SuperPoint 的训练数据也没看到,这些都是复现 SuperPoint 的核心。
(1)Homographic Adaptation 中对特征点结合的方法
原文中只看到一句:When applying Homographic Adaptation to an image, we use the average response across a large number of homographic warps of the input image. 也许是对置信度取平均再用阈值筛选出最终的特征点坐标(很可能也没那么简单)。从上面 Homographic Adaptation 在 HPatches 上的效果提升图上也可以看出,不仅仅能够额外提取出一些潜在点,还会去掉一些冗余点,在质量和数量上同步提升效果。
(2)SuperPoint 和 Homographic Adaptation 的训练集单应性变换生成方法
The joint training of SuperPoint is also done on 240×320 grayscale COCO images. For each training example, a homography is randomly sampled. It is sampled from a more restrictive set of homographies than during Homographic Adaptation to better model the target application of pairwise matching (e.g., we avoid sampling extreme in-plane rotations as they are rarely seen in HPatches).
文中并没有具体说怎样条件的单应性变换算一个合适的。
3. SuperGlue
SuperGlue 的论文里面涉及到了图神经网络、最优运输问题、Transformer、注意力机制等不是特别了解的领域。看了一轮代码发现,其实这个匹配任务跟图像也没什么关系,网络的输入只需要两幅图像的特征点位置、置信度和描述符,图像本身的信息只需要个尺寸用来做标准化,(根据对NLP的粗浅了解)感觉完全可以把特征点当做词向量。
后续单独写一篇 SuperGlue