【NetTopologySuite类库】NTS与JTS一些问题整理
文章目录
- 介绍
- SO上有关的一些问答
-
- 1、多边形自相交情况处理
- 2、折线分割多边形
- 3、凹多边形转为凸多边形
- 4、合并多个几何图形
- 5、单个Polygon转为MultiPolygon
介绍
NTS是C#版的JTS(Java Topology Suite),两者的API相似,代码很容易相互转化。
所以一个功能能用JTS实现,也能在NTS中找到对应API来实现。
SO上有关的一些问答
NTS的基础功能很容易上手,可以参考之前写的一点内容。
有些略微复杂的功能在国内博客上找不到,但在Stack OVerflow中能找到,于是下面列举了一些在SO中搜过的,并试验有效或有所启发的问答。
1、多边形自相交情况处理
OGC规则本身不允许有自相交多边形,但是实际生产的数据中很可能会混有。在用NTS在进行某些空间运算(相交、合并等)时,由于涉及自相交多边形,往往会报错。所以需要提前处理自相交多边形,将其转化为非自相交的。
在NTS中,可以通过几何对象的属性IsValid来检查是否是自相交,true表示是符合OGC规则的,自相交的则属于false这一类。
关于报错举个例子:
蓝色区域的多边形POLYGON((-1 -0.5,-1 1.5,1.5 1.5,1.5 -0.5,-1 -0.5))和红色区域的多边形POLYGON ((2 0,2 1,1 1,1 -1,0 -1,0 0,2 0))作相交运算:

会报错:
NetTopologySuite.Geometries.TopologyException:“found non-noded intersection between LINESTRING(1 1, 1 -0.5) and LINESTRING(0 0, 1.5 0) [ (1, 0, NaN) ]”。
就是对于红色区域的多边形来说,线段GH和JE之间是没有交点的,但是在做相交运算时,则需要有交点,但需要的时候却发现没有,所以报找不到交点的错。
1、下面两个博客介绍了自交的情况的处理,但应用的图形有限:博客1,博客2。
此外,还有博客中提到(下面的问答1中也提到):对自相交多边形作一个距离为0的缓冲,得到的结果就是正常多边形了。
但经过试验:会丢失部分的多边形。
2、博客3,源自SO上的一篇问答:问答1。
里面的回答用JTS实现了多边形自交的分解,将自交的一个多边形,分解为多个多边形,即MultiPolygon。
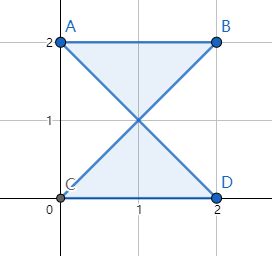
比如,下图多边形A-B-C-D-A为一个“沙漏形状”的自交多边形:
POLYGON((0 2, 2 2, 0 0, 2 0, 0 2))
下面是照样用NTS重写了SO中的JTS的代码,可以将“沙漏形状”变成两个多边形,即此处为两个三角形:
MULTIPOLYGON (((0 2, 2 2, 1 1, 0 2)), ((1 1, 2 0, 0 0, 1 1)))
public static IGeometry Validate(IGeometry geom)
{
if (geom.OgcGeometryType == OgcGeometryType.Polygon)
{
if (geom.IsValid)
{
geom.Normalize();
return geom;
}
Polygonizer polygonizer = new Polygonizer();
AddPolygon((Polygon)geom, polygonizer);
return ToPolygonGeometry(polygonizer.GetPolygons(), geom.Factory);
}
else if (geom.OgcGeometryType == OgcGeometryType.MultiPolygon)
{
if (geom.IsValid)
{
geom.Normalize(); // validate does not pick up rings in the wrong order - this will fix that
return geom; // If the multipolygon is valid just return it
}
Polygonizer polygonizer = new Polygonizer();
for (int i = 0; i < geom.NumGeometries; i++)
{
AddPolygon((Polygon)geom.GetGeometryN(i), polygonizer);
}
return ToPolygonGeometry(polygonizer.GetPolygons(), geom.Factory);
}
else
{
return geom; // In my case, I only care about polygon / multipolygon geometries
}
}
/**
* Add all line strings from the polygon given to the polygonizer given
* @param polygon polygon from which to extract line strings
* @param polygonizer polygonizer
*/
private static void AddPolygon(Polygon polygon, Polygonizer polygonizer)
{
//添加外边界线
addLineString(polygon.ExteriorRing, polygonizer);
//添加内边界线
foreach (var line in polygon.InteriorRings)
{
addLineString(line, polygonizer);
}
}
/**
* Add the linestring given to the polygonizer
* @param linestring line string
* @param polygonizer polygonizer
*/
private static void addLineString(ILineString lineString, Polygonizer polygonizer)
{
// LinearRings are treated differently to line strings : we need a LineString NOT a LinearRing
lineString = lineString.Factory.CreateLineString(lineString.CoordinateSequence);
// unioning the linestring with the point makes any self intersections explicit.
IGeometry toAdd = null;
IPoint point = lineString.Factory.CreatePoint(lineString.GetCoordinateN(0));
toAdd = lineString.Union(point);
//for (int i = 0; i < lineString.NumPoints; i++)
//{
// IPoint point = lineString.Factory.CreatePoint(lineString.GetCoordinateN(i));
// toAdd = lineString.Union(point);
//}
//Add result to polygonizer
polygonizer.Add(toAdd);
return;
}
/**
* Get a geometry from a collection of polygons.
*
* @param polygons collection
* @param factory factory to generate MultiPolygon if required
* @return null if there were no polygons, the polygon if there was only one, or a MultiPolygon containing all polygons otherwise
*/
private static IGeometry ToPolygonGeometry(ICollection<IGeometry> polygons, IGeometryFactory factory)
{
switch (polygons.Count)
{
case 0:
return null; // No valid polygons!
case 1:
return polygons.ElementAt(0); // single polygon - no need to wrap
default:
return factory.CreateMultiPolygon(polygons.Select(p => p as IPolygon).ToArray()); // multiple polygons - wrap them
}
}
3、还可以将下图中的自交多边形A-B-C-D-E-F-A:
POLYGON((0 0, 1 1, 2 0, 3 0, 4 1,5 0,0 0))
MULTIPOLYGON (((0 0, 1 1, 2 0, 0 0)), ((3 0, 4 1, 5 0, 3 0)))
2、折线分割多边形
computational geometry - Split a Polygon with a LineString in JTS - Stack Overflow
3、凹多边形转为凸多边形
computational geometry - Split concave polygon in convex ones - Stack Overflow
4、合并多个几何图形
java - Combining WKT geometries via union in JTS - Stack Overflow
5、单个Polygon转为MultiPolygon
casting - jts convert single polygon to multipolygon - Stack Overflow