数学知识——组合计数
组合计数
文章目录
- 组合计数
-
- 概述
- 动态规划
-
- 牡牛和牝牛
-
- 思路
- 代码
- 隔板法
-
- 方程的解
-
- 思路
- 代码
- 序列统计
-
- 思路
- 代码
- 加法 & 乘法原理
-
- 加法原理
- 乘法原理
- 车的摆放
-
- 思路
- 代码
- 容斥原理
-
- 数三角形
-
- 思路
- 代码
- Devu和鲜花
-
- 思路
- 代码
- 卡特兰数
-
- 网格
-
- 思路
- 代码
- 总结
概述
组合计数的目标是,计数某一类数学对象。
常用的方法有,dp、加法&乘法原理、容斥原理、卡特兰数等。
动态规划
牡牛和牝牛
约翰要带 N 只牛去参加集会里的展示活动,这些牛可以是牡牛,也可以是牝牛。
牛们要站成一排,但是牡牛是好斗的,为了避免牡牛闹出乱子,约翰决定任意两只牡牛之间至少要有K 只牝牛。
请计算一共有多少种排队的方法,所有牡牛可以看成是相同的,所有牝牛也一样,答案对 5000011 取模。
输入格式
一行,输入两个整数 N 和 K。
输出格式
一个整数,表示排队的方法数。
数据范围
1≤N≤10^5,0≤K
4 2
输出样例:
6
样例解释
6
种方法分别是:牝牝牝牝,牡牝牝牝,牝牡牝牝,牝牝牡牝,牝牝牝牡,牡牝牝牡。
思路
对于 1 0 5 10^5 105的数据量,完全可以使用动态规划。
我们从dp的角度思考。
状态表示f[i] :
集合:表示i位置站牡牛时,1~i位置合法的站法集合
属性:num
状态计算:f[i] = sum(f[j]), j = 0 ~ i - k - 1
可以使用前缀和优化
代码
MOD = 5000011
N = 100010
f = [0] * N
s = [0] * N
n, m = map(int, input().split())
f[0], s[0] = 1, 1
for i in range(1, n + 1) :
f[i] = s[max(0, i - m - 1)] % MOD
s[i] = (s[i - 1] + f[i]) % MOD
print(s[n])
隔板法
如果把n个相同的元素分给m个不同的对象,每个对象至少有一个,问有多少种不同的分法的问题。
方程的解
佳佳碰到了一个难题,请你来帮忙解决。
对于不定方程 a1+a2+⋯+ak−1+ak=g(x),其中k≥1 且 k∈N∗,x 是正整数,g(x)=xxmod1000(即 xx
除以 1000 的余数),x,k 是给定的数。
我们要求的是这个不定方程的正整数解组数。
举例来说,当 k=3,x=2 时,方程的解分别为:
⎧⎩⎨a1=1a2=1a3=2 ⎧⎩⎨a1=1a2=2a3=1 ⎧⎩⎨a1=2a2=1a3=1
输入格式
有且只有一行,为用空格隔开的两个正整数,依次为 k,x。
输出格式
有且只有一行,为方程的正整数解组数。
数据范围
1≤k≤100,1≤x<231,k≤g(x)
输入样例:
3 2
输出样例:
3
思路
x x x^x xx使用快速幂直接求解,剩下就是裸的隔板法的板子 C g ( x ) − 1 k − 1 C_{g(x) - 1}^{k - 1} Cg(x)−1k−1
代码
'''
对于g(x)使用快速幂计算
计算出结果,使用隔板法,计算结果
对于g(x)最多为1000,且查询次数较少,可以直接暴力
'''
from math import factorial
def qmi(a, k) :
res = 1
while k :
if k & 1 :
res = res * a % 1000
k >>= 1
a = a * a % 1000
return res
def c(a, b) :
return factorial(a) //(factorial(a - b) * factorial(b))
n, m = map(int, input().split())
print(c(qmi(m, m) - 1, n - 1))
序列统计
给定三个整数 N,L,R,统计长度在 1 到 N 之间,元素大小都在 L 到 R 之间的单调不降序列的数量。
输出答案对 106+3 取模的结果。
输入格式
输入第一行包含一个整数 T,表示数据组数。
第二到第 T+1 行每行包含三个整数 N,L,R。
输出格式
输出包含 T 行,每行有一个数字,表示你所求出的答案对 106+3 取模的结果。
数据范围
0≤N,L,R≤109,1≤T≤100,
输入数据保证 L≤R。
输入样例:
2
1 4 5
2 4 5
输出样例:
2
5
样例解释
对于第一组输入,满足条件的两个序列为 {4},{5}。
思路
枚举长度k: a 1 ≤ a 2 ≤ , . . . , ≤ a k a_1 \le a_2 \le ,...,\le a_k a1≤a2≤,...,≤ak,将所有都平移到 [ 0 , R − L ] [0, R - L] [0,R−L]
将其映射为差分 x i = a i − a i − 1 x_i = a_i - a_{i - 1} xi=ai−ai−1,则 x i ≥ 0 x_i \geq 0 xi≥0, ∑ i = 1 k x i ≤ R − L \sum_{i = 1}^kx_i \le R-L ∑i=1kxi≤R−L,若 x i + = 1 x_i += 1 xi+=1,则 x i > 0 x_i > 0 xi>0, ∑ i = 1 k x i ≤ R − L + 1 + k \sum_{i = 1}^kx_i \le R-L+1 + k ∑i=1kxi≤R−L+1+k,因为这里是不等式,所以不需要全部分配完,所以要额外添加一个板子。此时的计数为 C R − L + k k C_{R - L + k}^k CR−L+kk。最终答案为
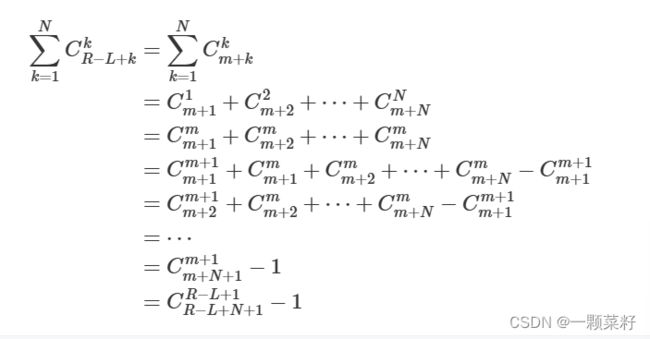
对于很大的数进行组合数计算使用卢卡斯定理
代码
MOD = int(1e6) + 3
def qmi(a, k) :
res = 1
while k :
if k & 1 :
res = res * a % MOD
k >>= 1
a = a * a % MOD
return res
def C(a, b) :
if a < b :
return 0
up, down = 1, 1
j = a
for i in range(1, b + 1) :
up = up * j % MOD
down = down * i % MOD
j -= 1
return up * qmi(down, MOD - 2) % MOD
def lucas(a, b) :
if a < MOD and b < MOD :
return C(a, b)
return C(a % MOD, b % MOD) * lucas(a // MOD, b // MOD) % MOD
T = int(input())
for _ in range(T) :
n, l, r = map(int, input().split())
print(lucas((r - l + n + 1, r - l + 1) - 1) % mod)
加法 & 乘法原理
加法原理
完成一个工程可以有 n 类办法, a i ( 1 ≤ i ≤ n ) a_i(1 \le i \le n) ai(1≤i≤n) 代表第 i 类方法的数目。那么完成这件事共有 S = a 1 + a 2 + ⋯ + a n S=a_1+a_2+\cdots +a_n S=a1+a2+⋯+an 种不同的方法。
乘法原理
完成一个工程需要分 n 个步骤, a i ( 1 ≤ i ≤ n ) a_i(1 \le i \le n) ai(1≤i≤n)代表第 i 个步骤的不同方法数目。那么完成这件事共有 S = a 1 × a 2 × ⋯ × a n S = a_1 \times a_2 \times \cdots \times a_n S=a1×a2×⋯×an 种不同的方法。
车的摆放
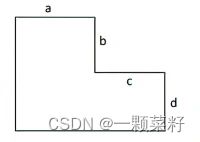
有下面这样的一个网格棋盘,a,b,c,d
表示了对应边长度,也就是对应格子数。
当 a=b=c=d=2 时,对应下面这样一个棋盘:
要在这个棋盘上放 k 个相互不攻击的车,也就是这 k 个车没有两个车在同一行,也没有两个车在同一列,问有多少种方案。
只需要输出答案 mod100003 后的结果。
输入格式
共一行,五个非负整数 a,b,c,d,k。
输出格式
包括一个正整数,为答案 mod100003 后的结果。
数据范围
0≤a,b,c,d,k≤1000,保证至少有一种可行方案。
输入样例:
2 2 2 2 2
输出样例:
38
思路
对于这个放置车的工程,对于这个不规则图形,我们可以将其分割成两块 a ∗ b a * b a∗b和 ( a + c ) ∗ d (a + c) * d (a+c)∗d图形,摆k辆车,通过枚举第一块放置的车的个数i,就可以确定第二块放置的车的个数k - i。两块放置的不同步骤可以利用乘法原理 C b i ∗ A a i ∗ C d i ∗ C a + c − i k − i C_b^i * A_a^i * C_d^i * C_{a + c - i}^{k- i} Cbi∗Aai∗Cdi∗Ca+c−ik−i得到总的方案。对于每一个i是完成这一工程的一个方法,利用加法原理 ∑ i = 0 k C b i ∗ A a i ∗ C d i ∗ C a + c − i k − i \sum_{i = 0}^kC_b^i * A_a^i * C_d^i * C_{a + c - i}^{k- i} ∑i=0kCbi∗Aai∗Cdi∗Ca+c−ik−i获得总的方案。
代码
N = 2010
MOD = 100003
fact = [0] * N
infact = [0] * N
def qmi(a, k) :
res = 1
while k :
if k & 1 :
res = res * a % MOD
k >>= 1
a = a * a % MOD
return res
def init(n) :
fact[0] = 1
infact[0] = 1
for i in range(1, n + 1) :
fact[i] = i * fact[i - 1] % MOD
infact[i] = qmi(i, MOD - 2) * infact[i - 1] % MOD
init(N - 1)
def C(a, b) :
if a < b : return 0
return fact[a] * infact[a - b] * infact[b] % MOD
def A(a, b) :
if a < b : return 0
return fact[a] * infact[a - b] % MOD
a, b, c, d, k = map(int, input().split())
res = 0
for i in range(k + 1) :
res = (res + C(b, i) * A(a, i) * C(d, k - i) * A(a + c - i, k - i)) % MOD
print(res)
容斥原理
数三角形
给定一个 n×m 的网格,请计算三点都在格点上的三角形共有多少个。
下图为 4×4 的网格上的一个三角形。
注意:三角形的三点不能共线。
输入格式输入一行,包含两个空格分隔的正整数m
和 n。
输出格式
输出一个正整数,为所求三角形数量。
数据范围
1≤m,n≤1000
输入样例:
2 2
输出样例:
76
思路
大概思路,所有点中取3个的方案数 C ( m + 1 ) ∗ ( n + 1 ) 3 C_{(m + 1) * (n + 1)}^3 C(m+1)∗(n+1)3 - 三点共线的方案数
三点共线的方案数分情况
- 斜率为0或者无穷大时: ( n + 1 ) ∗ C m + 1 3 + ( m + 1 ) ∗ C n + 1 3 (n + 1) * C_{m+1}^3 + (m + 1) * C_{n + 1}^3 (n+1)∗Cm+13+(m+1)∗Cn+13
- 斜率大于0或者小于0时:通过枚举左下角和右上角的点的横纵坐标的距离 ( i , j ) (i, j) (i,j),形成一个共线情况的方法有 ( g c d ( i , j ) − 1 ) (gcd(i, j) - 1) (gcd(i,j)−1)个,同样的距离可能的情况有 ( n + 1 − i ) ∗ ( m + 1 − j ) (n + 1 - i) * (m + 1- j) (n+1−i)∗(m+1−j)。对于所有(i, j)的枚举都是一种方案,符合加法原理。
代码
def C(a) :
if a < 3 :
return 0
return a * (a - 1) * (a - 2) // 6
def gcd(a, b) :
return a if b == 0 else gcd(b, a % b)
m, n = map(int, input().split())
m, n = m + 1, n + 1
res = C(m * n) - n * C(m) - m * C(n)
for i in range(1, n + 1) :
for j in range(1, m + 1) :
res -= 2 * (gcd(i, j) - 1) * (n - i) * (m - j)
print(res)
Devu和鲜花
Devu 有 N个盒子,第 i 个盒子中有 Ai 枝花。
同一个盒子内的花颜色相同,不同盒子内的花颜色不同。Devu 要从这些盒子中选出 M 枝花组成一束,求共有多少种方案。
若两束花每种颜色的花的数量都相同,则认为这两束花是相同的方案。
结果需对 10^9+7 取模之后方可输出。
输入格式
第一行包含两个整数 N 和 M。
第二行包含 N 个空格隔开的整数,表示 A1,A2,…,AN。
输出格式
输出一个整数,表示方案数量对 109+7 取模后的结果。
数据范围
1≤N≤20,0≤M≤1014,0≤Ai≤1012
输入样例:
3 5
1 3 2
输出样例:
3
思路
假设第i个盒子取出 x i x_i xi朵花,则满足 0 ≤ x i ≤ A i , ∑ 1 N x i = M 0\le x_i\le A_i,\sum_1^Nx_i=M 0≤xi≤Ai,∑1Nxi=M。将 x i x_i xi映射为 y i = x i + 1 y_i = x_i + 1 yi=xi+1,则满足 1 ≤ y i ≤ A i + 1 , ∑ 1 N y i = M + N 1 \le y_i\le A_i + 1, \sum_1^Ny_i=M + N 1≤yi≤Ai+1,∑1Nyi=M+N。若每个盒子无限制,则可以采用隔板法求得方案S: C M + N − 1 N − 1 C_{M + N - 1}^{N - 1} CM+N−1N−1。设 S i S_i Si为第i个盒子取到了超过 A i A_i Ai枝的方案数。
采用容斥原理得: a n s = S − ∑ S i + ∑ s ! = j S i U S j + . . . + . . . . ans = S - \sum S_i + \sum_{s !=j} S_i U S_j + ...+ .... ans=S−∑Si+∑s!=jSiUSj+...+....
对于 S i U S j U . . . S_i U S_j U... SiUSjU...表示为 C M + N − 1 − ( A i + 1 ) − ( A j + 1 ) − . . . . N − 1 C_{M + N - 1 - (A_i+ 1) - (A_j+ 1) - ....}^{N-1} CM+N−1−(Ai+1)−(Aj+1)−....N−1
这个式子共 2 n 2^n 2n项,通过枚举 1 < < n 1 << n 1<<n可得出所有情况。
代码
MOD = int(1e9) + 7
N = 25
A = [0] * N
def qmi(a, k) :
res = 1
while k :
if k & 1 :
res = res * a % MOD
k >>= 1
a = a * a % MOD
return res
def C(a) :
if a < n - 1 :
return 0
j = a
up = 1
for i in range(1, n) :
up = up * j % MOD
j -= 1
return up * qmi(down, MOD - 2) % MOD
down = 1
n, m = map(int, input().split())
for i in range(1, n) :
down = down * i % MOD
A[:n] = list(map(int, input().split()))
# 容斥原理
res = 0
for i in range(1 << n) :
sign = 1
a = n + m - 1
for j in range(n) :
if i >> j & 1 :
sign *= -1
a -= A[j] + 1
res = (res + sign * C(a)) % MOD
print(res)
卡特兰数
一般题目具有的性质是,任意前缀中的某属性的值小于等于另一属性值
网格
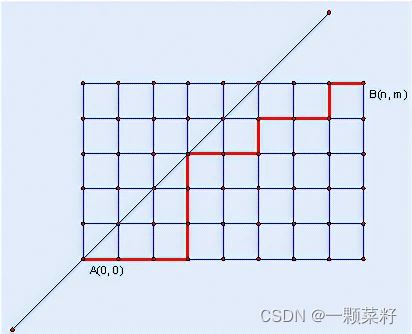
某城市的街道呈网格状,左下角坐标为 A(0,0),右上角坐标为 B(n,m),其中 n≥m。
现在从 A(0,0) 点出发,只能沿着街道向正右方或者正上方行走,且不能经过图示中直线左上方的点,即任何途径的点 (x,y) 都要满足 x≥y,请问在这些前提下,到达 B(n,m) 有多少种走法。
输入格式
仅有一行,包含两个整数 n 和 m,表示城市街区的规模。
输出格式
输出一个整数,表示不同的方案总数。
数据范围
1≤m≤n≤5000
输入样例:
6 6
输出样例:
132
思路
卡特兰数:终点 ( n , m ) (n, m) (n,m) 关于 y = x + 1 y = x + 1 y=x+1对称点(m - 1, n + 1)
a n s = C n + m m ( 总走法 ) − C n + m m − 1 ( 不合法走法 ) ans = C_{n + m}^{m}(总走法) - C_{n + m}^{m - 1}(不合法走法) ans=Cn+mm(总走法)−Cn+mm−1(不合法走法)
代码
from math import factorial
def C(a, b) :
if a < b :
return 0
return factorial(a) // (factorial(a - b) * factorial(b))
n, m = map(int, input().split())
print(C(n + m, m) - C(n + m, m - 1))
总结
组合计数题目一般特点N特别大,一定要发掘题目中的性质orz。