动态规划专题精讲1

致前行的人：

                要努力，但不要着急，繁花锦簇，硕果累累都需要过程！

前言：

        本篇文章为大家带来一种重要的算法题，就是动态规划类型相关的题目，动态规划类的题目在笔试和面试中是考察非常高频的一类，要想掌握这一类的题目就需要在掌握正确的学习方法的前提下做大量的练习，下面为大家介绍几道动态规划中比较经典的题目，每一道题目都有非常详细的思路实现，看完相信大家一定会有收获的！

1.动态规划概念：

动态规划，英⽂：Dynamic Programming，简称DP，如果某⼀问题有很多重叠⼦问题，使⽤动态规划是最有效的，动态规划中每⼀个状态⼀定是由上⼀个状态推导出来的

2.动态规划解题步骤

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

3.动态规划应该如何调试

找问题的最好⽅式就是把dp数组打印出来，看看究竟是不是按照⾃⼰思路推导的，做动规的题⽬，写代码之前⼀定要把状态转移在dp数组的上具体情况模拟⼀遍，⼼中有数，确定最后推出的是想要的结果。

然后再写代码，如果代码没通过就打印dp数组，看看是不是和⾃⼰预先推导的哪⾥不⼀样。如果打印出来和⾃⼰预先模拟推导是⼀样的，那么就是⾃⼰的递归公式、初始化或者遍历顺序有问题了。如果和⾃⼰预先模拟推导的不⼀样，那么就是代码实现细节有问题。

4.动态规划经典题目

斐波那契数 oj链接

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

思路：

按照动规五部曲依次推导

这⾥我们要⽤⼀个⼀维dp数组来保存递归的结果
1. 确定dp数组以及下标的含义
dp[i]的定义为：第i个数的斐波那契数值是dp[i]
2. 确定递推公式
为什么这是⼀道⾮常简单的⼊门题⽬呢？
因为题⽬已经把递推公式直接给我们了：状态转移⽅程 dp[i] = dp[i - 1] + dp[i - 2];
3. dp数组如何初始化
题⽬中把如何初始化也直接给我们了，如下：

dp[0] = 0;
dp[1] = 1;

4. 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍
历的顺序⼀定是从前到后遍历的
5. 举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2]，我们来推导⼀下，当N为10的时候，dp数组应
该是如下的数列：
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来，发现结果不对，就把dp数组打印出来看看和我们推导的数列是不是⼀致的。
以上我们⽤动规的⽅法分析完了，C++代码如下：

class Solution {
public:
    int fib(int n) 
    {
        if(n <= 1)
            return n;
        vector dp(n+1);
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2; i <= n; i++)
        {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

爬楼梯oj链接

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

思路：

爬到第⼀层楼梯有⼀种⽅法，爬到⼆层楼梯有两种⽅法。那么第⼀层楼梯再跨两步就到第三层 ，第⼆层楼梯再跨⼀步就到第三层。
所以到第三层楼梯的状态可以由第⼆层楼梯 和 到第⼀层楼梯状态推导出来，那么就可以想到动态规划了。

动规五部曲：
定义⼀个⼀维数组来记录不同楼层的状态
1. 确定dp数组以及下标的含义
dp[i]： 爬到第i层楼梯，有dp[i]种⽅法
2. 确定递推公式
如果可以推出dp[i]呢？
从dp[i]的定义可以看出，dp[i] 可以有两个⽅向推出来。
⾸先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种⽅法，那么再⼀步跳⼀个台阶不就是dp[i]了么。
还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种⽅法，那么再⼀步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候，⼀定要时刻想着dp[i]的定义，否则容易跑偏。这体现出确定dp数组以及下标的含义的重要性！
3. dp数组如何初始化
在回顾⼀下dp[i]的定义：爬到第i层楼梯，有dp[i]中⽅法。
那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但都基本是直接奔着答案去解释的。
例如强⾏安慰⾃⼰爬到第0层，也有⼀种⽅法，什么都不做也就是⼀种⽅法即：dp[0] = 1，相当于直接站在楼顶。
但总有点牵强的成分。
那还这么理解呢：我就认为跑到第0层，⽅法就是0啊，⼀步只能⾛⼀个台阶或者两个台阶，然⽽楼层是0，直接站楼顶上了，就是不⽤⽅法，dp[0]就应该是0.
其实这么争论下去没有意义，⼤部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过，然后就往结果上靠去解释dp[0] = 1。
从dp数组定义的⾓度上来说，dp[0] = 0 也能说得通。
需要注意的是：题⽬中说了n是⼀个正整数，题⽬根本就没说n有为0的情况。
所以本题其实就不应该讨论dp[0]的初始化！
我相信dp[1] = 1，dp[2] = 2，这个初始化⼤家应该都没有争议的。
所以我的原则是：不考虑dp[0]如果初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。
4. 确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序⼀定是从前向后遍历的
5. 举例推导dp数组
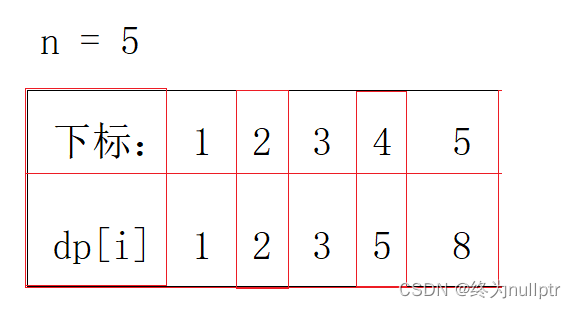
举例当n为5的时候，dp table（dp数组）应该是这样的

如果代码出问题了，就把dp table 打印出来，看看究竟是不是和⾃⼰推导的⼀样。此时⼤家应该发现了，这不就是斐波那契数列么！唯⼀的区别是，没有讨论dp[0]应该是什么，因为dp[0]在本题没有意义！
以上五部分析完之后，C++代码如下：

class Solution {
public:
    int climbStairs(int n) {
        if(n <= 1)
            return n;
        vector dp(n+1);
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3; i <= n; i++)
        {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

使用最小花费爬楼梯oj链接

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。
示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。
- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
- 支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

思路：

使用动规五部曲：

1. 确定dp数组以及下标的含义

到达第i个台阶所花费的最少体⼒为dp[i]

2. 确定递推公式

题目描述中说，可以选择向上一次爬一个台阶或者一次爬两个台阶，所以到达第i阶台阶，可以通过第i-1阶台阶到达或者是通过第i-1阶台阶到达，然后在根据题目描述求的是达到顶楼所需要花费的最小体力，所以递推公式可以推导出：

dp[i] = min(dp[i-1]+cost[i-1] + dp[i-2]+cost[i-2])

3. dp数组如何初始化

题目描述说，可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，也就是说到下标为0的台阶和到下标为1的台阶是不需要花费体力的，所以应该初始化为：

dp[0] = 0;                        dp[1] = 0;

4. 确定遍历顺序

本题的遍历顺序很简单，从前往后依次遍历就可以了

5.打印dp数组：

以上分析完毕，整体C++代码如下：

class Solution {
public:
    int minCostClimbingStairs(vector& cost) {
        vectordp(cost.size()+1);
        dp[0] = 0;
        dp[1] = 0;
        for(int i = 2; i <= cost.size(); i++)
        {
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.size()];
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

不同路径oj链接

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28
示例 2：

 

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
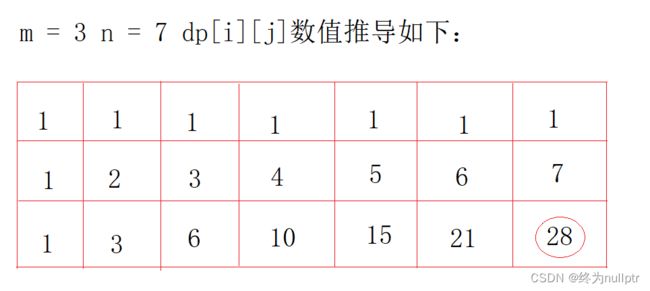
示例 3：

输入：m = 7, n = 3
输出：28
示例 4：

输入：m = 3, n = 3
输出：6

思路：

机器⼈从(0 , 0) 位置触发，到(m - 1, n - 1)终点。
按照动规五部曲来分析：

1. 确定dp数组以及下标的含义

dp[i][j] ：表⽰从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2. 确定递推公式

根据题目中的描述机器人每次只能向下或者向右移动一步，所以到达dp[i][j]的路径总数是到达dp[i-1][j]的路径总数加上到达dp[i][j-1]的路径总数之和，所以递推公式应该为：dp[i][j] = dp[i-1][j] + dp[i][j-1]

3.dp数组的初始化

⾸先dp[i][0]⼀定都是1，因为从(0, 0)的位置到(i, 0)的路径只有⼀条，那么dp[0][j]也同理。

所以初始化代码为：

for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;

4. 确定遍历顺序

这⾥要看⼀下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上⽅和左⽅推导⽽来，那么从左到右⼀层⼀层遍历就可以了。

5. 举例推导dp数组

如图所示：

以上动规五部曲分析完毕，C++代码如下：

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector>dp;
        dp.resize(m);
        for (int i = 0; i < dp.size(); i++)
        {
            dp[i].resize(n, 0);
        }
        //初始化第一列：
        for (int i = 0; i < m; i++)
        {
            dp[i][0] = 1;
        }
        //初始化第一行：
        for (int j = 0; j < n; j++)
        {
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

时间复杂度：O(m * n)
空间复杂度：O(m * n)

不同路径2oj链接

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2：

 
输入：obstacleGrid = [[0,1],[0,0]]
输出：1

思路：

通过动规五部曲来进行分析：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j] ：表⽰从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2. 确定递推公式

递推公式和62.不同路径⼀样，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。

但这⾥需要注意⼀点，因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）。

所以代码为：

if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候，再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}

3. dp数组如何初始化

因为从(0, 0)的位置到(i, 0)的路径只有⼀条，所以dp[i][0]⼀定为1，dp[0][j]也同理。但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是⾛不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。

 下标(0, j)的初始化情况同理。所以本题初始化代码为：

vector> dp(m, vector(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

注意代码⾥for循环的终⽌条件，⼀旦遇到obstacleGrid[i][0] == 1的情况就停⽌dp[i][0]的赋值1的操作，dp[0][j]同理

4. 确定遍历顺序

从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出，⼀定是从左到右⼀层⼀层遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]⼀定是有数值。

代码如下：

for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}

5. 举例推导dp数组

动规五部分分析完毕，对应C++代码如下：

class Solution {
public:
    int uniquePathsWithObstacles(vector>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector>dp;
        dp.resize(m);
        for(int i = 0; i < dp.size(); i++)
        {
            dp[i].resize(n,0);
        }
        //初始化第一行：
        for(int i = 0; i < n; i++)
        {
            if(obstacleGrid[0][i] == 1)
                break;
            dp[0][i] = 1; 
        }
        //初始化第一列：
        for(int j = 0; j < m; j++)
        {
            if(obstacleGrid[j][0] == 1)
                break;
            dp[j][0] = 1;
        }
        for(int i = 1; i < m; i++)
        {
            for(int j = 1; j < n; j++)
            {
                if(obstacleGrid[i][j] == 1)
                    continue;
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

时间复杂度O(n * m) n m 分别为obstacleGrid 长度和宽度
空间复杂度O(n * m)

整数拆分oj链接

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

思路：

使用动规五部曲进行分析：

1. 确定dp数组（dp table）以及下标的含义

dp[i]：分拆数字i，可以得到的最⼤乘积为dp[i]。

2. 确定递推公式

可以想 dp[i]最⼤乘积是怎么得到的呢？其实可以从1遍历j，然后有两种渠道得到dp[i].
⼀个是j * (i - j) 直接相乘。
⼀个是j * dp[i - j]，相当于是拆分(i - j)

那么从1遍历j，⽐较(i - j) * j和dp[i - j] * j 取最⼤的。
递推公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));

3. dp的初始化

dp[0] dp[1]应该初始化多少呢？
有的题解⾥会给出dp[0] = 1，dp[1] = 1的初始化，但解释⽐较牵强，主要还是因为这么初始化可以把题⽬过了。
严格从dp[i]的定义来说，dp[0] dp[1] 就不应该初始化，也就是没有意义的数值。
拆分0和拆分1的最⼤乘积是多少？这是⽆解的。
这⾥我只初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最⼤乘积是1，这个没有任何异议！

4. 确定遍历顺序

确定遍历顺序，先来看看递归公式：dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));dp[i] 是依靠 dp[i - j]的状态，所以遍历i⼀定是从前向后遍历，先有dp[i - j]再有dp[i]。枚举j的时候，是从1开始的。i是从3开始，这样dp[i - j]就是dp[2]正好可以通过我们初始化
的数值求出来。

所以遍历顺序为

for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}

5. 举例推导dp数组

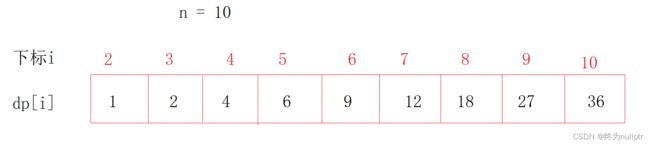
举例当n为10 的时候，dp数组⾥的数值，如下：

以上动规五部曲分析完毕，C++代码如下：

class Solution {
public:
    int integerBreak(int n)
    {
        vector dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n; i++)
        {
            for (int j = 1; j < i - 1; j++)
            {
                dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
};

时间复杂度：O(n^2)
空间复杂度：O(n)

不同的二叉搜索树oj链接

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

思路：

这道题⽬描述很简短，但估计⼤部分同学看完都是懵懵的状态，这得怎么统计呢？面对这道题，我们应该画画图，看看有没有什么规律

 

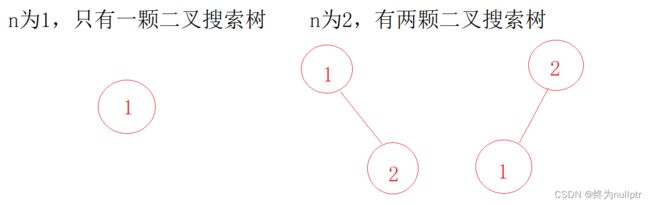
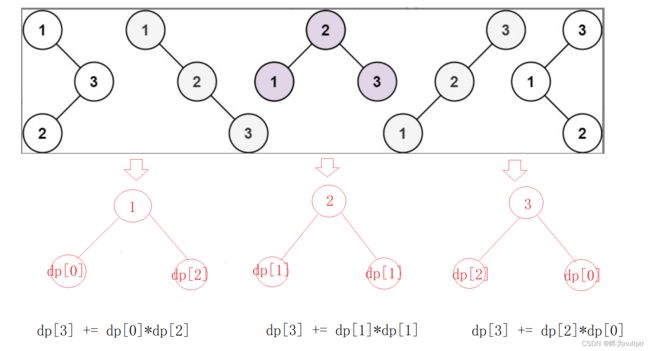
 n为3，可以有5颗二叉搜索树：

来看看n为3的时候，有哪⼏种情况。

当1为头结点的时候，其右⼦树有两个节点，看这两个节点的布局，是不是和 n 为2的时候两棵树的布局是⼀样的啊！

（可能有同学问了，这布局不⼀样啊，节点数值都不⼀样。别忘了我们就是求不同树的数量，并不⽤把搜索树都列出来，所以不⽤关⼼其具体数值的差异）

当3为头结点的时候，其左⼦树有两个节点，看这两个节点的布局，是不是和n为2的时候两棵树的布局也是⼀样的啊！

当2位头结点的时候，其左右⼦树都只有⼀个节点，布局是不是和n为1的时候只有⼀棵树的布局也是⼀样的啊！

发现到这⾥，其实我们就找到的重叠⼦问题了，其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种⽅式。
思考到这⾥，这道题⽬就有眉⽬了。

dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量

元素1为头结点搜索树的数量 = 右⼦树有2个元素的搜索树数量 * 左⼦树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右⼦树有1个元素的搜索树数量 * 左⼦树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右⼦树有0个元素的搜索树数量 * 左⼦树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。

所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

如图所示：

 此时我们已经找到的递推关系了，那么可以⽤动规五部曲在系统分析⼀遍。

1. 确定dp数组（dp table）以及下标的含义

dp[i] ： 1到i为节点组成的⼆叉搜索树的个数为dp[i]。

2. 确定递推公式

在上⾯的分析中，其实已经看出其递推关系， dp[i] += dp[以j为头结点左⼦树节点数量] *dp[以j为头结点右⼦树节点数量]
j相当于是头结点的元素，从1遍历到i为⽌。

所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左⼦树节点数量，i-j 为以j为头结点右⼦树节点数量

3. dp数组如何初始化

初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]。那么dp[0]应该是多少呢？
从定义上来讲，空节点也是⼀颗⼆叉树，也是⼀颗⼆叉搜索树，这是可以说得通的。

4. 确定遍历顺序

⾸先⼀定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i⾥⾯每⼀个数作为头结点的状态，⽤j来遍历。

代码如下：

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
        dp[i] += dp[j - 1] * dp[i - j];
    }
}

5. 举例推导dp数组

n为5时候的dp数组状态如图：

 综上分析完毕，C++代码如下：

class Solution {
public:
    int numTrees(int n) {
        vectordp(n+1);
        dp[0] = 1;
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= i; j++)
            {
                dp[i] += dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
};

时间复杂度O(n^2)
空间复杂度O(n)