飞桨DeepXDE用例验证及评估

在之前发布的文章中，我们介绍了飞桨全量支持业内优秀科学计算深度学习工具 DeepXDE。本期主要介绍基于飞桨动态图模式对 DeepXDE 中 PINN 方法用例实现、验证及评估的具体流程，同时提供典型环节的代码，旨在帮助大家更加高效地基于飞桨框架进行科学计算用例建设与调试。

用例验证及评估标准

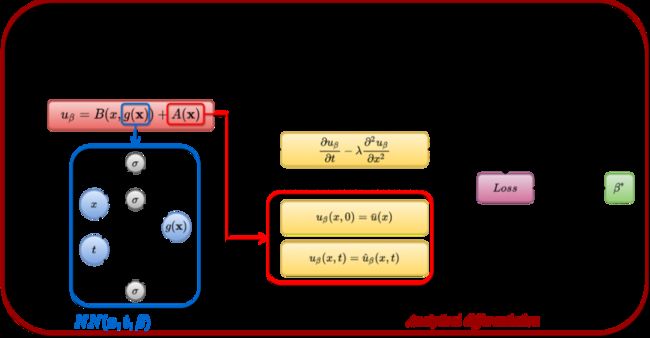
PINN（Physics-Informed Neural Network）是一种融合神经网络和物理机理的深度学习方法，可用于求解各类微分方程（PDE/ODE/IDE/FPDE等）描述的物理问题。如下图所示，PINN方法可应用于正问题与逆问题场景。在正问题求解中，可根据自变量和相关参数求解物理方程中的因变量信息，如流场中的速度、压力等信息；在逆问题求解中，根据自变量同时求解方程中的因变量和反演相关参数，如基于部分监督数据可对流场的速度、压力等信息进行预测，同时逆向反演控制方程中的密度、粘度等未知参数。更多关于PINN方法的信息，可参考飞桨公众号专题文章“飞桨加速CFD（计算流体力学）原理与实践”。

PINN方法基础原理  

相关链接：

https://en.wikipedia.org/wiki/Physics-informed_neural_networks

针对DeepXDE中提供的44个PINN方法用例，飞桨目前实现了全量支持，而PyTorch目前支持31个。基于飞桨对DeepXDE中全量用例进行验证及评估的过程中，我们在DeepXDE作者陆路老师的指导下，依据用例中的物理方程是否已知解析解（标签值）制定了两种验证及评估方法，即“基于训练结果与解析解的误差”和“基于网络损失函数值”。具体如下：

基于训练结果与解析解的误差

针对已知科学计算问题中物理机理方程解析解的情况，可以直接使用飞桨进行科学计算问题的物理机理方程求解，并计算训练解（网络输出）相对于解析解（真值）的误差（如RMSE_Loss、L2_Loss等），从而对飞桨求解结果进行验证。当RMSE_Loss结果小于10^-2时，通常可认为飞桨框架对此用例的验证符合要求。

此外，在使用飞桨对DeepXDE中的用例进行结果评估时，若训练解（网络输出）与解析解的误差结果RMSE_Loss不小于10^-2，同时该用例提供了其他框架的公开验证结果，可进行对比评估。若飞桨与其他同类框的RMSE_Loss接近，则说明当前测试用例的精度主要与其本身算法实现有关，飞桨计算的训练解符合当前测试用例的本身精度。若要进一步提升训练解的精度，则需要修改官方用例的求解算法。

基于训练网络的损失函数值

针对未知科学计算问题中物理机理方程解析解的情况，使用飞桨进行收敛性测试时，由于缺少可参考的解析解或标签值，将训练过程中损失函数RMSE_Loss下降的量级作为模型是否收敛的判断标准。一般情况下，我们需要对初始loss值进行归一化，当训练过程中loss值下降至10^-4量级时认为模型收敛。

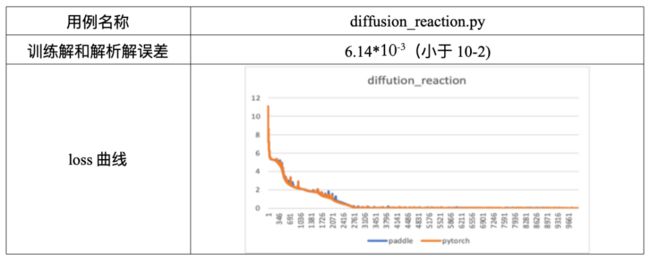
在完成飞桨框架收敛自测后，若对应的用例已经在其他框架（如PyTorch或TensorFlow）上进行了公开测试，也可进一步对比飞桨与同类框架的loss收敛曲线，评估它们之间的相似度。首先，需要保证不同框架之间loss收敛曲线吻合，即图像上无明显不吻合的片段；其次，当loss的绝对值大于1时，要求飞桨与同类框架loss值之间的相对误差达到10^-6量级，当loss值下降至1以下后，若loss值的相对误差达到10^-5量级，也可认为合理（绝对误差达到10^-6量级）。

用例验证及评估流程

用例实现

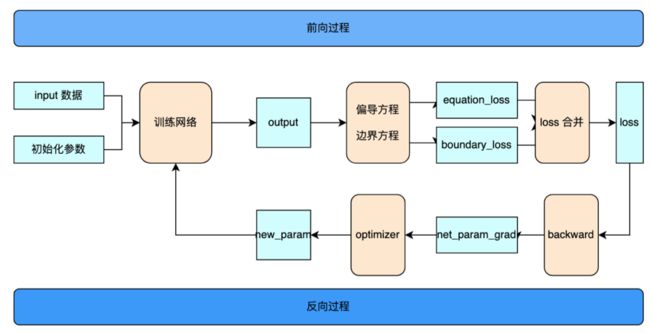
采用PINN方法的用例训练过程如下图所示。图中蓝色部分为网络参数更新所需要验证和评估的数据（若需要进行同类框架对比时），黄色部分为用例实现的具体逻辑。

用例训练过程

按照图中步骤，基于PINN方法建设用例需要逐次实现训练网络、偏导方程及边界方程、loss合并计算、反向传播、网络参数更新。下面结合DeepXDE中的PINN方法用例，具体介绍其实现流程。

训练网络

目前PINN方法通常使用全连接神经网络, 可通过继承paddle.nn.Layer来实现各类方法的应用。网络输入数据为物理机理方程的自变量，输出数据为微分方程的因变量。具体地，以基于Navier-Stokes方程求解稳态流场问题为例，输入数据包括时空坐标（x, y, z），而输出数据则包括速度和压力信息（u, v, w, p）。

值得注意的是，DeepXDE提供的部分用例在全连接网络中增加了transform的处理，因此在继承paddle.nn.Layer来定义全连接网络时，需要在网络中定义transform接口，详见《附录-class NN》。

在网络结构初始化时，需要给定网络层数、各层参数、激活函数以及参数初始化方法等，如下面代码所示。用户可灵活设置以上参数的传递方式，详见《附录-class FNN》。用户可实例化以上网络，并调用forward函数进行训练。

偏导方程和边界方程‍

PINN方法用例的核心是采用物理机理方程和初边值方程（条件）来调整训练网络的优化方向。这些方程多为各类微分方程，可使用飞桨提供的自动微分接口grad()实现。同时为了便于用户调用，DeepXDE基于grad()接口封装了Jacobian和Hessian接口，分别支持一阶和二阶微分计算，具体可见DeepXDE中dde.grad.hessian()、dde.grad.jacobian() API的定义。通过Jacobian和Hessian接口的自由组合，可以实现任意阶微分计算。

利用以上接口，用户可定义偏微分方程以及边界方程，相应代码示意如下：

def Possion(x，y):
    dy_xx = dde.grad.hessian(y，x)
    return -dy_xx - np.pi ** 2 * bkd.sin(np.pi * x)

在完成方程定义后，可基于训练网络的输入和输出计算相应的loss值，相应代码示意如下：

equation_loss = pde(inputs，outputs_)
boundary_condition_loss = boundary(inputs，outputs_)

loss计算、反向传播及参数更新

• Loss计算

在进行一次前向计算后，可按照权重对方程、边界、数据等各类loss进行加权计算，从而得到单次训练步下的总loss，相应代码示意如下：

loss = paddle.sum(equation_loss ，boundary_condition_loss)

• 反向传播

反向传播过程会对前向计算过程所涉及的算子进行更高一阶的微分运算，利用微分算子，可以从输出层开始，逐层计算每个神经元对误差的贡献，并将误差分摊到每个神经元上，相应代码示意如下：

loss.backward()

• 参数更新

在使用优化算法对网络进行优化后，会对网络参数进行更新，并用于下一次前向计算，相应代码示意如下：

paddle.optimizer.Adam.step()
paddle.optimizer.Adam.clear_grad()

用例验证

在完成用例实现后，即可按照2.1与2.2小节中描述的用例验证评估标准开展。

单独框架自测验证

若已知物理机理方程的解析解，则可直接基于飞桨对用例进行“单独框架自测”，并确保用例中网络被训练至收敛，同时保留loss数据以及测试集对应的预测解。进一步地，可按照2.1节中的标准验证是否满足与解析解的精度要求。若缺少解析解，则可按照2.2节中的标准来评估loss收敛是否满足要求。

同样，若缺少物理方程解析解，且单独框架自测无法满足精度要求时，可查看DeepXDE中该用例是否在同类框架上进行了公开测试。若有，则可定义飞桨使用与同类框架相同的训练网络、网络初始参数以及网络的输入数据，并与该用例的训练结果和网络参数进行逐轮对比。

验证注意点 

• 初始化参数固定

正常训练过程中，一般随机初始化训练网络的相关参数。为确保多次训练具有相同的初始化参数和样本点数据，需要固定全局随机数，相应代码示意如下：

dde.set_random_seed (100)

• 初始化参数统一

针对已经在同类框架公开结果的用例，在使用飞桨进行用例验证及评估时，应统一飞桨与其他框架生成的初始化参数，而不能使用NumPy生成的数据作为初始化参数（可能导致loss极大，影响判断）。如基于PyTorch实现的部分PINN求解用例中，《附录-框架参数转换》提供了PyTorch参数转换为飞桨参数的函数，支持用户保存同类框架的网络参数。在飞桨读取初始化参数文件时，建议从参数文件中按照字符串读取的方式对齐初始化参数，同时利用vimdiff确认参数是否设置一致。在模型代码中加入读取网络参数的代码，并运行生成初始化参数，可以保存参数数据至Init_param.log，具体可见《附录-模型参数保存》。 随后运行命令 python3.7 example.py Init_param.log ，即可读入相应的网络参数。 

在飞桨的神经网络中实现初始化参数导入以及将网络参数数值存入文件的代码详见《附录-初始化参数读入》。其中，__init__() 函数的接口需要传入处理后的list w_array，b_array。

• 统一验证策略

针对已经在同类框架公开结果的用例，在使用飞桨进行用例验证及评估时可对比飞桨与同类框的loss结果曲线，并将两个框架的相对误差输出至diff.log文件中，相关代码可参考《附录-对比脚本》。当验证不通过时，优先更换激活函数，测试不同的网络构成是否存在相同问题；然后，逐步对比前向过程和反向过程，查找潜在问题。具体参见“5 典型用例验证”。

用例问题排查方法

当用例实现存在问题时，可对比同类框架中用例实现过程（若存在公开的测试结果），进行前向和反向的逐步对比验证。按照2.1节中的流程图，打印所有模块的中间输出，定位diff模块。为保证精度以及控制相关变量，验证之前需做如下设置：

设置1（随机数种子）

由于用例中存在随机生成样本的算法，因此需要固定全局的随机种子，保证每次生成的样本数据一致。

设置2 (数据类型）

由于float32的数据只有6-7位有效数字是有意义的，因此在做单步比较时，需要将全局数据类型设置为float64, 从而可以对得到的结果进行逐位对齐（float64的有效数字位数为16-17）。在DeepXDE中，可通过加入如下代码来设置：

dde.config.set_default_float('float64')

设置3（初始化参数）

飞桨中参数初始化器paddle.nn.initializer.Assign 不支持float64类型，需替换为paddle.nn.initializer.Constant，且初值不建议取0、1等特殊值。相关代码示意如下：

weight_attr_ = paddle.ParamAttr(initializer = paddle.nn.initializer.Constant(0.2345))
self.linears.append(paddle.nn.Linear(layer_sizes[i - 1]，layer_sizes[i]，weight_attr=weight_attr_，bias_attr=False))

‍‍

同类框架也需要做相应的设置，如PyTorch可参考如下代码：

self.linears.append(
    torch.nn.Linear(layer_sizes[i - 1]，layer_sizes[i]，bias=False，dtype=torch.float64)
)
torch.nn.init.constant_(self.linears[-1].weight.data，0.2345)

‍‍

设置4（控制合理误差）

PINN方法中训练网络结构相对简单，使用层数不多的全连接网络层，但不同框架内部kernel的实现方式不同。例如，PyTorch和飞桨在matmul的高阶微分kernel实现上方式不同，因此计算的结果会有正常的误差。为避免相加以及顺序不同引起的误差，在调试时，可以设置隐藏层大小为2，这样matmul中计算每个结果的加法只有一次，不存在加和顺序的影响。

设置5（降低验证难度）

在验证过程中可通过一系列方法来降低验证难度，如：减少网络层数、去掉linear层的bias设置、减少边界方程、降低偏导方程的阶数、减少偏导方程的算子等。

注意：由于同类框架的高阶算子和飞桨的高阶算子实现方式不同，相应的反向图也不同，从而导致参数的梯度不同，这些误差无法避免，其量级一般在10^-6。这类误差只在个别用例中出现，具体查验需要打印框架log，画出反向图，分析参数梯度的贡献算子。

• 前向打印数据

网络输入数据、初始化参数、网络输出数据、equation_loss、bc_loss、loss等，可参考《附录-对比脚本》对各部分的数据进行对比。在上述设置下，前向过程的所有数据都应该严格逐位一致。当某一步出现diff时，可以定位其上一流程出现问题，按照设置5中的方式逐步控制变量来查验问题。

• 反向打印数据

参数的梯度和更新后的参数同样可参考以上对比脚本对各部分的数据进行对比，若出现误差，则需要分析反向图，查看是否是注意点中的合理误差。

典型用例验证结果评估

在使用飞桨进行DeepXDE中PINN用例的验证及评估时，结合用例已有验证情况，如是否已知解析解、是否具备公开的同类框架验证结果等，可能会出现多种情况。如下所示，并给出了相应的结果评估说明。

满足解析解精度要求

飞桨训练解满足解析解精度，同时Loss曲线也满足验证要求，即飞桨训练最后的结果满足精度要求。此部分用例完全基于飞桨框架独立验证，代表的用例如Poisson、Burgers等。

未满足解析解精度要求

飞桨在对DeepXDE中的个别用例进行验证时，训练解不满足解析解精度要求，若此用例已经在同类框架上进行了公开的测试，可对比飞桨训练的loss曲线与同类框架的loss曲线吻合情况，有如下可能：

• loss曲线吻合

我们可增加不同框架间的解析解和训练解差距的对比图，当图像吻合或差距小于10^-3时，也视为满足要求。

• loss曲线后期出现波动

该情况大概率是因为用例中模型具有周期性特点，从而导致拟合函数不够平滑。但不同框架之间的解析解和训练解差距对比图相近时，也可认为满足验证验证及评估要求。在与同类框架对比验证过程中，若loss曲线出现比较明显的差异，可尝试更换多组初始化参数进行验证，同时也可能是模型本身对初始化参数敏感导致了loss的不稳定。

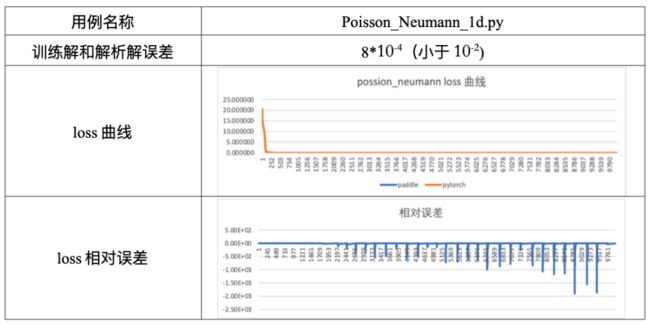
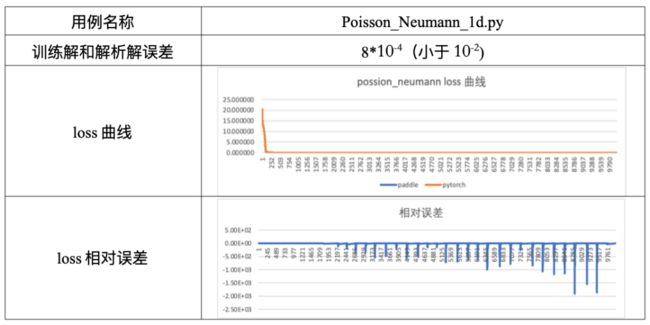
• Loss 曲线中间出现部分波动，导致曲线没有严格吻合

飞桨在部分用例验证过程中，前200步满足和同类框架的loss相对误差在^10-6以内，且最终loss收敛值小于10^-4，但loss曲线在中间有波动且不同框架波动的位置不同。对此我们可认为该用例网络模型拟合的曲线不够平滑，存在震荡点，且不同框架开始震荡的时间有差异，导致loss曲线无法严格吻合，这种情况不影响最终收敛。

对于同类问题，loss曲线波动较大的情况，建议从波动点获取参数作为初始化参数重新训练。

总结

本期重点介绍了如何基于飞桨对DeepXDE中提供的PINN用例进行实现、验证及评估，结合用例具备的条件（如解析解、公开测试结果等）进行飞桨独立框架测试以及对比部分同类框架等。在进行用例验证及评估的同时，我们对飞桨进行了性能优化，在所验证的用例中，75%的用例性能超越了同类框架PyTorch，最高提升高达25%，具体可见：

https://mp.weixin.qq.com/s/yBsuLWozN4AJCFO5grJ8WA

希望本期内容可为使用飞桨进行科学计算用例实现、调试以及代码复现等工作的同学提供帮助，也非常欢迎大家沟通讨论~

附录

• class NN

class NN(paddle.nn.Layer):
    """Base class for all neural network modules."""
    def __init__(self):
        super().__init__()
        self._input_transform = None
        self._output_transform = None
    def apply_feature_transform(self，transform):
        """Compute the features by appling a transform to the network inputs，i.e.,
        features = transform(inputs). Then，outputs = network(features).
        """
        self._input_transform = transform
    def apply_output_transform(self，transform):
        """Apply a transform to the network outputs，i.e.,
        outputs = transform(inputs，outputs).
        """
        self._output_transform = transform

‍

• class FNN

class FNN(NN):
    """Fully-connected neural network."""
    def __init__(self，layer_sizes，activation，kernel_initializer):
        super().__init__()
        self.activation = activations.get(activation)
        self.layer_size = layer_sizes
        initializer = initializers.get(kernel_initializer)
        initializer_zero = initializers.get("zeros")
        self.linears = paddle.nn.LayerList()
        for i in range(1，len(layer_sizes)):
            self.linears.append(
                paddle.nn.Linear(
                    layer_sizes[i - 1],
                    layer_sizes[i],
                )
            )
            initializer(self.linears[-1].weight)
            initializer_zero(self.linears[-1].bias)
    def forward(self，inputs):
        x = inputs
        if self._input_transform is not None:
            x = self._input_transform(x)
        for linear in self.linears[:-1]:
            x = self.activation(linear(x))
        x = self.linears[-1](x)
        if self._output_transform is not None:
            x = self._output_transform(inputs，x)
        return x
inputs = paddle.to_tensor(inputs, stop_gradient=False)
outputs_ = self.net(inputs)
self.net.train()

• 框架参数转换

这里以PyTorch为例，linear层的参数与飞桨的参数互为转置，代码如下：

import numpy as np
import torch
import paddle
def torch2paddle():
    torch_path = "./data/mobilenet_v3_small-047dcff4.pth"
    paddle_path = "./data/mv3_small_paddle.pdparams"
    torch_state_dict = torch.load(torch_path)
    fc_names = ["classifier"]
    paddle_state_dict = {}
    for k in torch_state_dict:
        if "num_batches_tracked" in k:
            continue
        v = torch_state_dict[k].detach().cpu().numpy()
        flag = [i in k for i in fc_names]
        if any(flag) and "weight" in k: # ignore bias
            new_shape = [1，0] + list(range(2，v.ndim))
            print(f"name: {k}，ori shape: {v.shape}，new shape: {v.transpose(new_shape).shape}")
            v = v.transpose(new_shape)
        k = k.replace("running_var"，"_variance")
        k = k.replace("running_mean"，"_mean")
        # if k not in model_state_dict:
        if False:
            print(k)
        else:
            paddle_state_dict[k] = v
    paddle.save(paddle_state_dict，paddle_path)
if __name__ == "__main__":
    torch2paddle()

• ‍模型参数保存

layer_size = [2] + [num_dense_nodes] * num_dense_layers + [2]
# paddle init param
w_array = [] // linear层的所有weight数据
b_array = [] // linear层的所有bias数据
input_str = [] 
file_name1 = sys.argv[1]
with open(file_name1，mode='r') as f1:
    for line in f1:
        input_str.append(line)
j = 0
for i in range(1，len(layer_size)):
    shape_weight = (layer_size[i-1]，layer_size[i])
    w_line = input_str[j]
    w = []
    tmp = w_line.split(',')
    for num in tmp:
        w.append(np.float(num))
    w = np.array(w).reshape(shape_weight)
    w_array.append(w)
    print("w . shape :"，w.shape)
    j = j+1
    bias_weight = (layer_size[i])
    b_line = input_str[j]
    b = []
    tmp = b_line.split(',')
    for num in tmp:
        b.append(np.float(num))
    b = np.array(b).reshape(bias_weight)
    b_array.append(b)
    print("b . shape :"，b.shape)
    j = j+1

• 初始化参数读入

def __init__(self，layer_sizes，activation，kernel_initializer，w_array=[]，b_array=[]):
    super().__init__()
    self.activation = activations.get(activation)
    initializer = initializers.get(kernel_initializer)
    initializer_zero = initializers.get("zeros")
    self.linears = paddle.nn.LayerList()
    for i in range(1，len(layer_sizes)):
        weight_attr_ = paddle.ParamAttr(initializer = paddle.nn.initializer.Assign(w_array[i-1]))
        bias_attr_ = paddle.ParamAttr(initializer = paddle.nn.initializer.Assign(b_array[i-1]))
        self.linears.append(paddle.nn.Linear(layer_sizes[i - 1]，layer_sizes[i],weight_attr=weight_attr_，bias_attr=bias_attr_))

    # 参数输出为文件
    if paddle.in_dynamic_mode():
        import os
        f = open('paddle_dygraph_param.log','ab')
        for linear in self.linears:
            np.savetxt(f,linear.weight.numpy().reshape(1,-1),delimiter=",")
            np.savetxt(f,linear.bias.numpy().reshape(1,-1),delimiter=",")
        f.close()

‍

• 同类框架对齐代码

这里仍然以PyTorch为例，其与飞桨对齐的代码如下：

def __init__(self，layer_sizes，activation，kernel_initializer，w_array=[]，b_array=[]):
        super().__init__()
        self.activation = activations.get(activation)
        initializer = initializers.get(kernel_initializer)
        initializer_zero = initializers.get("zeros")
        self.linears = torch.nn.ModuleList()
        for i in range(1，len(layer_sizes)):
            print("init i :"，i，"self.linears :"，self.linears)
            self.linears.append(
                torch.nn.Linear(
                    layer_sizes[i - 1]，layer_sizes[i]，bias=False，dtype=torch.float64
                )
            )
            self.linears[-1].weight = torch.nn.parameter.Parameter(torch.Tensor(w_array[i-1]).transpose(0,1))
            self.linears[-1].bias = torch.nn.parameter.Parameter(torch.Tensor(b_array[i-1]))
        import os
        f = open('pytorch_param.log','ab')
        for linear in self.linears:
            # general initilizer :
            tmp0 = linear.weight.cpu().detach().numpy()
            tmp0 = np.transpose(tmp0)
            np.savetxt(f,tmp0.reshape(1,-1),delimiter=",")
            np.savetxt(f,tmp1.reshape(1,-1),delimiter=",")
        f.close()

• 对比脚本

import sys
import numpy as np
file_name1 = sys.argv[1]
file_name2 = sys.argv[2]
comp_file_name = sys.argv[3]
paddle_data=[]
pytorch_data=[]
with open(file_name1，mode='r') as f1:
    for line in f1:
        #pytorch_data.append(float(line))
        tmp = line.split(',')
        for num in tmp:
            pytorch_data.append(float(num))
with open(file_name2，mode='r') as f2:
    for line in f2:
        tmp = line.split(',')
        for num in tmp:
            paddle_data.append(float(num))
compare_data=[]
for i in range(len(pytorch_data)):
    if pytorch_data[i] == 0.0:
        tmp = np.inf
    else:
        tmp = (pytorch_data[i] - paddle_data[i]) / pytorch_data[i]
    compare_data.append(tmp)
with open(comp_file_name，mode='w') as f3:
    compare_data = np.array(compare_data)
    np.savetxt(f3,compare_data)

引用

[1] 飞桨全量支持业内AI科学计算工具——DeepXDE!

https://mp.weixin.qq.com/s/yBsuLWozN4AJCFO5grJ8WA

[2] DeepXDE介绍文档

https://deepxde.readthedocs.io/en/latest/

[3] 飞桨加速CFD（计算流体力学）原理与实践

拓展阅读

[1] 使用飞桨高阶自动微分功能探索AI+结构领域科研

[2] 飞桨科学计算实训示例

https://aistudio.baidu.com/aistudio/projectoverview/public?topic=15

[3] 飞桨黑客松第四期任务—科学计算专题

https://github.com/PaddlePaddle/Paddle/issues/51281#science

相关地址

[1]飞桨AI for Science共创计划

https://www.paddlepaddle.org.cn/science

[2]飞桨PPSIG Science小组

https://www.paddlepaddle.org.cn/specialgroupdetail?id=9

关注【飞桨PaddlePaddle】公众号

获取更多技术内容~