图解通俗理解对比学习(Contrastive Learning)中的温度系数（temperature）

1. 对比学习简述

没有学过对比学习的，请学一下，这里只是复习。

对比学习目的：让相似的样本在空间中距离近一点，让不相似的样本距离远一点。这样就可以让特征分布在空间中更加均匀。

对比学习方法：

1. 构建一个正样本对儿 $(x_i,x_j)$ ，和负样本对儿 $(x_i,y_j)$ ，其中$x_i$和$x_j$为相似的样本（例如两张狗的图片），而$x_i$和$y_j$为不相似的样本（例如狗和猫的图片）。
2. 为了让相似的样本在空间中距离更近，不相似的样本在空间中更远，可以使用相似度函数(通常使用余弦相似度(cosine similarity))计算的相似度，即 $\text{sim}(x_i,x_j)$越大越好，$\text{sim}(x_i,y_j)$ 越小越好

这里的 $x_i$ 称为锚点，$x_j$ 称为正样本，$y_j$称为负样本

对比学习的Loss：

1. 对比学习的Loss和多分类是一样的，都是使用的CrossEntropyLoss。

为什么使用CrossEntropyLoss可行呢，我们不妨来想一下多分类是怎么做的。

在多分类中，假设我们有4个类别，$[c_1,c_2,c_3,c_4]$，假设我们的输出为 $y=[y_1,y_2,y_3,y_4]$，若当前样本为$c_1$类别，那么我们则是希望 $y_1$ 越大越好，$y_2,y_3,y_4$越小越好。

在对比学习中，假设我们有1个正样本 $(x_1^{\prime })$，3个负样本 $(y_2,y_3,y_4)$，那么使用样本 $x$ 与它们计算的样本相似度为 $[\text{sim}(x,x_1^{\prime }),\text{sim}(x,y_2),\text{sim}(x,y_3),\text{sim}(x,y_4)]$，此时我们同样是想让 $\text{sim}(x,x_1^{\prime })$ 越大越好，其他的越小越好呢。

所以，对比学习也使用CrossEntropyLoss。对比学习损失函数写作：

$$L_c=-\log \frac{\exp \left(\mathrm{sim}\left(x,x_i^{\prime }\right)/\tau \right)}{{\sum }_{j=1}^n\exp \left(\mathrm{sim}\left(x,y_j\right)/\tau \right)}$$

虽然每个论文的公式写不太一样，但表达的意思都是一样的。

2. 直观感受下对比学习

为了感受对比学习的作用，我们将使用如下代码进行演示。

首先导入需要用到的包：

import matplotlib.pyplot as plt
import torch
from torch import nn
import random
import numpy as np
import torch.nn.functional as F
from tqdm import tqdm
import copy

定义一些两个工具类：

def setup_seed(seed):
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    np.random.seed(seed)
    random.seed(seed)
    torch.backends.cudnn.deterministic = True

"""用于绘制样本"""
def plot_samples(samples, labels):
    plt.xlim(-1.1, 1.1)
    plt.ylim(-1.1, 1.1)

    plt.scatter(samples[labels==0, 0], samples[labels==0, 1], color='blue')
    plt.scatter(samples[labels==1, 0], samples[labels==1, 1], color='yellow')
    plt.scatter(samples[labels==2, 0], samples[labels==2, 1], color='black')
    plt.scatter(samples[labels==3, 0], samples[labels==3, 1], color='red')

    plt.annotate("", xy=(1, 0), xycoords='data', xytext=(-1, 0), textcoords='data',
                 arrowprops=dict(arrowstyle="->", connectionstyle="arc3"))  # 画x轴
    plt.annotate("", xy=(0, 1), xycoords='data', xytext=(0, -1), textcoords='data',
                 arrowprops=dict(arrowstyle="->", connectionstyle="arc3"))  # 画y轴
    plt.show()

setup_seed(0) # 设置随机种子

---

接下来正式开始对比学习演示。

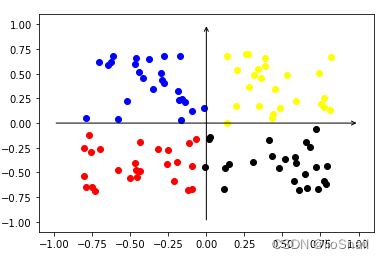
这里我们定义100个样本，每个样本有两个特征(x, y)，Label有(0,1,2,4)，即所属的象限：

samples = torch.rand(100, 2)
samples[25:50, 0] -= 1
samples[50:75, :] -= 1
samples[75:100, 1] -= 1
labels = torch.LongTensor([0] * 25 + [1] * 25 + [2] * 25 + [3] * 25)

绘制我们的样本，如下：

plot_samples(samples, labels)

之后我们定义一个encoder来模拟卷积网络、BERT等负责提取特征的backbone：

encoder = nn.Sequential(
    nn.Linear(2, 10, bias=False),
    nn.Linear(10, 2, bias=False),
    nn.Tanh()
)

经过encoder后，我们会提取样本的特征，绘制到图中如下：

plot_samples(encoder(samples).clone().detach(), labels)

从图上我们可以看到我们的encoder提取的特征都挤在一起了，这对于后续网络的分类很不利，所以对比学习就派上用场了，让相似的样本离得近一点，不相似的样本距离远一点，最终可以做到均匀分布。

这里举得例子不够好，因为相似样本距离已经很近了。

我们首先准备一下使用对比学习训练encoder的代码：

def train_and_plot(step=10000, temperature=0.05):
	"""
	step: 训练次数
	temperature：温度系数
	"""
    encoder_ = copy.deepcopy(encoder)	# 这里复制一个encoder，别污染原来的encoder，因为后面要做对比实验
    loss_fnt = nn.CrossEntropyLoss()
    optimizer = torch.optim.SGD(encoder_.parameters(), lr=3e-4)

	# 训练step次，简单期间，这里batch_size=1
    for _ in tqdm(range(step)):
        anchor_label = random.randint(0, 3)	# 从4个label里随机挑出一种作为anchor
        anchor_sample = samples[labels == anchor_label][random.sample(range(25), 1)]  # 从anchor样本中随机挑出一个样本
        positive_sample = samples[labels == anchor_label][random.sample(range(25), 1)] # 从anchor样本中再挑出一个做成正样本
        negative_samples = samples[labels != anchor_label][random.sample(range(75), 3)] # 从其他样本中挑出3个作为负样本

		# 使用encoder提取各个样本的特征
        anchor_feature = encoder_(anchor_sample)
        positive_feature = encoder_(positive_sample)
        negative_feature = encoder_(negative_samples)

		# 计算anchor与正样本和负样本的相似度
        positive_sim = F.cosine_similarity(anchor_feature, positive_feature)
        negative_sim = F.cosine_similarity(anchor_feature, negative_feature)
		
		# 将正样本和负样本concat起来，再除以温度参数
        sims = torch.concat([positive_sim, negative_sim]) / temperature
        # 构建CrossEntropyLoss的Label，因为我把正样本放在了第0个位置，所以Label为0
        sims_label = torch.LongTensor([0])	
		
		# 计算CrossEntropyLoss
        loss = loss_fnt(sims.unsqueeze(0), sims_label.view(-1))
        loss.backward()
		# 更新参数
        optimizer.step()
        optimizer.zero_grad()
	
	# 绘制训练后的结果。
    plot_samples(encoder_(samples).clone().detach(), labels)

接下来使用0.05的温度参数训练一下encoder，然后重新绘制samples的特征向量：

train_and_plot(10000, temperature=0.05)

可以看到，经过对比学习后，特征分布更加均匀了。

3. 对比学习不同温度系数比较

上一节我们准备了一个对比学习的训练函数，所以只需要使用不同的参数就能进行比较：

train_and_plot(10000, temperature=0.99)
train_and_plot(10000, temperature=0.5)
train_and_plot(10000, temperature=0.05)
train_and_plot(10000, temperature=0.01)
train_and_plot(10000, temperature=0.001)

最终我们得到如下图：

最后的0.001温度系数点看起来很少并不是因为点消失或出界了，而是因为网络使用了Tanh激活函数，将特征限制在了(-1, 1)之间，所以样本点都集中在了 $(-1,1)$ 和 $(-1,-1)$ 这两个位置。

结论

从上图中可以看出如下结论：

1. 温度参数越小，对比学习效果越强，即对比学习让相似样本距离就会越近，不相似样本距离越远
2. 若想要让样本特征分布均匀，温度参数需要适中，太大和太小都不好。

4. 对比学习结论分析

之所以会出现上述的结果，其实很容易分析，我们只需要看一下不同参数的求Loss过程中的变化即可。

假设我们的锚点样本和正负样本的相似度如下：

$[\text{sim}(x,x_1^{\prime }),\text{sim}(x,y_2),\text{sim}(x,y_3),\text{sim}(x,y_4)]$ = [0.5, 0.25, -0.45, -0.1]

我们来看一下随着温度参数的变化，相似度、SoftMax的概率分布和CrossEntropyLoss都是如何变化的：

温度	sim	Softmax概率分布	CrossEntropyLoss
1	[0.5, 0.25, -0.45, -0.1]	[0.3684, 0.2869, 0.1425, 0.2022]	0.9986
0.5	[ 1.0, 0.5, -0.9, -0.2]	[0.4861, 0.2948, 0.0727, 0.1464]	0.7214
0.05	[10, 5, -9, -2]	[0.9933, 6.6e-03, 5.5e-09, 6.1-06]	0.0067
0.01	[ 50, 25, -45, -10]	[1.00, 1.3e-11, 5.5-42, 8.7-27]	0

你可以使用下面这段代码进行上述表格的实验：

t = 1	# 温度参数
sims = torch.tensor([0.5, 0.25, -0.45, -0.1]) / t
print(sims)
prob = F.softmax(sims, dim=-1)
print(prob)
loss = F.cross_entropy(sims.unsqueeze(0), torch.LongTensor([0]))
print(loss)

从上面的表格可以得到如下结论：

• 温度系数越低，概率分布就越陡。也就是在对比学习中经常看到的图：
  
  这个图可能看起来还不够清晰，如果用正态分布表示，则为：
  （此图并不严谨，是随便画的，主要用于感受温度变化对概率分布的调整）
  
• 当锚点与正样本的相似度最高时，温度系数越低，loss越低。

上述表格是假设了锚点与正样本的相似度最高，若锚点与某个负样本相似度低呢？

假设我们的锚点样本和正负样本的相似度如下：

$[\text{sim}(x,x_1^{\prime }),\text{sim}(x,y_2),\text{sim}(x,y_3),\text{sim}(x,y_4)]$ = [0.25, 0.5, -0.45, -0.1]

那么，随着温度参数的变化，相似度、SoftMax的概率分布和CrossEntropyLoss都是如何变化的：

温度	sim	Softmax概率分布	CrossEntropyLoss
1	[0.25, 0.5, -0.45, -0.1]	[0.2869, 0.3684, 0.1425, 0.2022]	1.2486
0.5	[ 0.5, 1.0, -0.9, -0.2]	[0.2948, 0.4861, 0.0727, 0.1464]	1.2214
0.05	[5, 10, -9, -2]	[ 6.6e-03, 0.9933, 5.5e-09, 6.1-06]	5.0067
0.01	[ 25, 50, -45, -10]	[1.3e-11, 1.00, 5.5-42, 8.7-27]	25

通过这两个表格，我们可以得到温度系数与Loss的关系：

1. 当锚点与正样本的相似度最高时，温度系数越低，loss越低。
2. 当锚点与某个负样本的相似度最高时，温度系数越低，loss越高。
3. 由1可知，当温度系数较高时，模型的调节相对温和，不论模型是否正确预测正样本，都会调节模型
4. 由2可知，当温度系数较低时，模型的调节比较锐利，模型偏向尽快学会预测正样本，学会后就几乎不再调节模型。

5. 温度系数结论

上述结论都是根据自己的理解与实验得出的，若有不严谨或错误的地方请各位在评论区指出。

温度系数的不同取值有以下结论：

1. 温度参数越小，对比学习效果越强，即对比学习让相似样本距离就会越近，不相似样本距离越远
2. 若想要让样本特征分布均匀，温度参数需要适中，太大和太小都不好。
3. 当锚点与正样本的相似度最高时，温度系数越低，loss越低。
4. 当锚点与某个负样本的相似度最高时，温度系数越低，loss越高。
5. 由1可知，当温度系数较高时，模型的调节相对温和，不论模型是否正确预测正样本，都会调节模型
6. 由4可知，当温度系数较低时，模型的调节比较锐利，模型偏向尽快让学会预测正样本，学会后就几乎不再调节模型。

1,2结论请参考第3节。3,4,5,6结论请参考第4节。

常用的温度系数是 0.05