图论：图的四种最短路径算法
目录：
1.DFS（单源最短路径算法）
例题1：
DFS题目分析：
代码DFS：
2.Floyed（时间复杂度On^3）
1.应用场景：
2.解析算法：
核心代码1：
我的笔记
核心代码2：
Floyd例题：
3.Dijksyta算法
1.应用场景：
2.算法描述：
1.初始化：
2.for：
核心代码：
3.例题：
注意：
代码如下：
4.SPFA算法
1.算法思想：
2.注意：
3.算法分析：
4.核心代码：
5.例题：
题目分析：
代码如下：
5.总结：
那让我为大家介绍这四种算法吧！
1.DFS（单源最短路径算法）
例题1：
建立一个有向图，n代表城市个数，有m行连接数据，x代表连接初始点，y代表连接点，r代表线权。求城市1到城市5的最短路径。
输入：
5 8
1 2 2
2 3 3
3 4 4
4 5 5
5 3 3
1 5 10
3 1 4
2 5 7输出：
9DFS题目分析：
用dfs进行搜索的话，递归的出口是什么？->
当然是扫描到最后一个城市的时候，然后记录下此时的路径值，如果之后搜索的测试值比之前的值小，则更新路径的值，搜索完所有的路径后，输出最小值，其中用VIS数组进行标记和回溯。
代码DFS：
#include
using namespace std;
//从城市1到城市5最短路径为多少？
int mp[105][105];//图
int vis[105];//测试数组
int x, y, r;
int n; int m;
int minx = 1000000;
void dfs(int step, int sum) {
if (sum > minx) {
return;
}
if (step == n) {//当扫描到最后一个城市时
if(sum> n>>m;
while (m--) {
cin >> x >> y >> r;
mp[x][y] = r;//该图为有向图，是由x到y的距离
}
dfs(1, 0);
cout << minx << endl;
} 2.Floyed（时间复杂度On^3）
1.应用场景：
1.多源最短路径。（缺点：时间复杂度相对较高，但是可以解决负权边问题）
2.找最小环。
3.倍增。
2.解析算法：
通过插入点和中转点来缩短路径，先将图中各点连线都初始化为无穷，再进行建图，中转所有的点，不断更新最小值输出：
核心代码1：
for (int k = 1; k <= n; k++) {//从1到n依次各点进行中转
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (e[i][j] > e[i][k] + e[k][j]) {//如果该路径更短，更新成该路径
e[i][j] = e[i][k] + e[k][j];
}
}
}
}我的笔记
然后就是我的笔记啦：（还是比较详细的）
这里由不得思考一个问题，Floyd算法无非就是动态规划，状态转移方程为![e[i][j]=max(e[i][j],e[i][k]+e[k][j])](http://img.e-com-net.com/image/info8/6c7591274dee4ec19ecee2ca273e0dd6.gif){kind=small}
核心代码2：
void floyed(){
for (int k = 1; k <= n; k++) {//从1到n依次各点进行中转
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (e[i][j] > e[i][k] + e[k][j]) {//如果该路径更短，更新成该路径
e[i][j] = max(e[i][j],e[i][k] + e[k][j]);
}
}
}
}
}Floyd例题：
AcWing 854 Floyd求最短路
题目描述：
给定一个n个点m条边的有向图，图中可能存在重边和自环，边权可能为负数。
再给定k个询问，每个询问包含两个整数x和y，表示查询从点x到点y的最短距离，如果路径不存在，则输出“impossible”。
数据保证图中不存在负权回路。
输入格式
第一行包含三个整数n，m，k
接下来m行，每行包含三个整数x，y，z，表示点x和点y之间存在一条有向边，边长为z。
接下来k行，每行包含两个整数x，y，表示询问点x到点y的最短距离。
输出格式
共k行，每行输出一个整数，表示询问的结果（最小路径），若询问两点间不存在路径，则输出“impossible”。
数据范围
1≤n≤200,
1≤k≤n^2
1≤m≤20000,
图中涉及边长绝对值均不超过10000。
输入：
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3输出：
impossible
1题目注意：
1.初始图矩阵的建立。
2.如果有重复的边如何处理。
3.输出的时候如何判断x，y没有路径。
代码如下：
#include
#include
using namespace std;
const int INF = 1e9;
int n, m, k;
int x, y, r;
int e[300][300];
void floyed() {
for (int k = 1; k <= n; k++) {//从1到n依次各点进行中转
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (e[i][j] > e[i][k] + e[k][j]) {//如果该路径更短，更新成该路径
e[i][j] = max(e[i][j], e[i][k] + e[k][j]);
}
}
}
}
}
int main()
{
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {//建立初始的图，赋值
for (int j = 1; j <= n; j++) {
if (i == j) {
e[i][j] = 0;
}
else {
e[i][j] = INF;
}
}
}
while (m--) {
cin >> x >> y >> r;
e[x][y] = min(e[x][y], r);//处理重复边的值
}
floyed();
while(k--)
{
cin >> x >> y;
if (e[x][y] > INF / 2) {//说明x到y没有路可以走
cout << "impossible" << endl;
}
else {
cout << e[x][y] << endl;//输出最短路径
}
}
}
今天的分享暂时先到这里，明天持续更新.....
3.Dijksyta算法
1.应用场景：
单源路径最短（我只看出来了这种）时间复杂度(On^2)
注意：不能求负权值.
2.算法描述：
设起点为x，dis[v]表示s到v的最短路径
1.初始化：
起点初始化为0。其余点初始化为无穷大
2.for：
a.在没有访问的顶点中找到一个顶点u，使得dis[u]是最小的。（不断搜索到下一个路径最小的点，更新）。
b.u为已确定的最短路径（将不再对该点及之前的点进行搜索）。
核心代码：
int dijkstra(int n, int m) {//n为顶点数，m为起点开始的位置
while (true) {
fill(dis, dis + maxn, INF);
dis[m] = 0;//初始化起点为0
int index = -1;
int minx = 0;//定义
for (int i = 1; i <= n; i++) {
if (!vis[i] && minx > dis[i]) {//寻找到该点
index = i;
minx = dis[i];
}
}
if (index == -1) {//说明没有点可以继续搜索了
break;//退出循环条件
}
vis[index] = 1;//已经确定该点为最短路径点了，标记上踢出
for (int j = 1; j <= n; j++) {
if (dis[j] > dis[index] + mp[index][j]&&vis[j]==0&&mp[index][j]!=INF) {//该点有路可以走
dis[j] = dis[index] + mp[index][j];//值得思考有DP思想
}
}
}
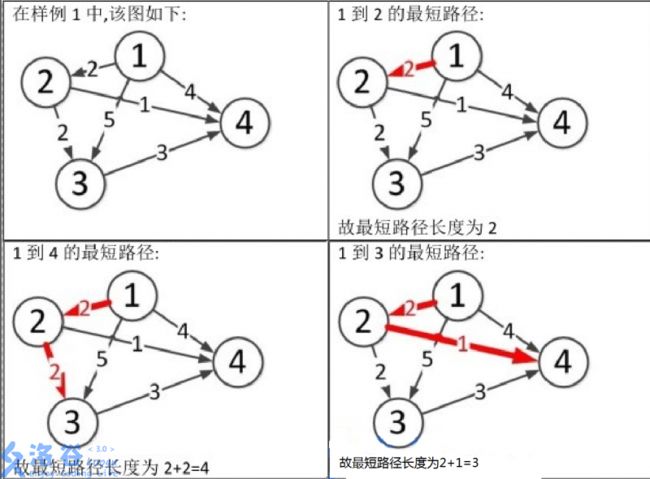
}3.例题：
（改题目来源于算法笔记）
题目要求：求V0到其他位置s的最短路径。
输入格式：
n为有几个顶点，m为几条边，s为起点。
第二行到第m+1行输入x,y,r，分别为x结点到y结点，边权为r。
输出格式：从s到个顶点的最短路径。
输入：
6 8 0
0 1 1
0 3 4
0 4 4
1 3 2
2 5 1
3 2 2
3 4 3
4 5 3输出：
0 1 5 3 4 6题目分析： 不断去找路径最短的那个顶点，标记，搜索下一个最短顶点即可。（图示->）
注意：
1.vis数组的标记。
2.更新顶点，没有路径的点就不进行扫描。
3.循环的终止条件。
代码如下：
#include
#include
#include
#include
using namespace std;
const int maxn = 1000;//规定一个最大顶点数
const int INF = 199999999;
int n, m, s;
int mp[maxn][maxn];
int dis[maxn];
bool vis[maxn] = { false };
void Dijkstra(int s) {
memset(dis, 0x7f, sizeof(dis));
dis[s] = 0;
for (int i = 1; i <= n; i++) {//循环了n次
int index = -1;
int minx = INF;
for (int j = 0; j < n; j++) {
if (vis[j] == false && dis[j] < minx) {
index = j;//记录这个搜索到的路径最小的点。
minx = dis[j];//更新最小值
}
}
if (index == -1) {//没有路可以走了
return;
}
vis[index] = true;//标记该点
for (int i = 0; i < n; i++) {
if (vis[i] == false && mp[index][i] != INF && dis[index] + mp[index][i] < dis[i]) {
dis[i] = dis[index] + mp[index][i];//优化更新dis[i]
}
}
}
}
int main() {
int x, y, r;
cin >> n >> m >> s;
memset(mp, 0x7f, sizeof(mp));
for (int i = 1; i <= m; i++) {
cin >> x >> y >> r;
mp[x][y] = r;
}
Dijkstra(s);//将起点输入进去
for (int i = 0; i < n; i++) {
cout << dis[i] << " ";
}
return 0;
}
完美撒花！继续更新SPFA算法。
4.SPFA算法
1.算法思想：
队列优化，去掉一些无用的松弛操作，用队列来维护松弛造作的点。继承了Bellman-Ford算法的思想，但时间复杂度相对来说提高了很多。
与BFS的算法有一些类似，利用了STL队列。
2.注意：
虽然大多数情况spfa跑的比较快，但时间复杂度仍为（Onm），主要用应用于有负边权的情况（如果没有负边权，推荐使用Dijkstra算法）。利用了邻接表建图，数据结构的基础一定要掌握好，而且该算法很容易超时，被卡，必须要谨慎选择该算法。
3.算法分析：
1.用dis数组记录点到有向图的任意一点距离，初始化起点距离为0，其余点均为INF，起点入队。
2.判断该点是否存在。（未存在就入队，标记）
3.队首出队，并将该点标记为没有访问过，方便下次入队。
4.遍历以对首为起点的有向边（t,i）,如果dis[i]>dis[t]+w(t,i),则更新dis[i]。
5.如果i不在队列中，则入队标记，一直到循环为空。
4.核心代码：
#include
#include
#include
using namespace std;
const int INF = 1000000000;
const int maxn = 1000;
int dis[maxn];//记录最小路径的数组
bool vis[maxn];//标记
struct node {
int s1;//记录结点
int side;//边权
};
vectormp[maxn];//用vector建立邻接表
void Spfa(int s) {
queuev;
vis[s] = 1; v.push(s); dis[s] = 0;
while (!v.empty()) {
int q = v.front();
v.pop(); vis[q] = 0;
for (int i = 0; i < mp[q].size(); i++) {
if (dis[mp[q][i].s1] > dis[q] + mp[q][i].side) {
dis[mp[q][i].s1] = dis[q] + mp[q][i].side;//更新最短路径。
if (!vis[mp[q][i].s1]) {//是在更新新的值条件里面判断，一定特别注意这点
v.push(mp[q][i].s1);
vis[mp[q][i].s1] = 1;//标记未标记过的点
}
}
}
}
} 完美撒花！！！
5.例题：
P3371 【模板】单源最短路径（弱化版） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目背景：
本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过（但本题可以用SPFA过），如有需要请移步 P4779
题目描述：
如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。
输入输出样例：
输入 ：
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4输出 ：
0 2 4 3
样例说明：
图片1到3和1到4的文字位置调换
题目分析：
建立一个有向图，输出s到第i个结点的最短距离。（无疑是套刚刚那个模板）
代码如下：
#include
using namespace std;
const int maxn = 10001;
const long long INF = 2147483647;
int dis[maxn];//记录最小路径的数组
int vis[maxn];//标记
int n, m, s;
struct node {
int s1;//记录结点
int side;//边权
};
void init() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
vis[i] = 0;
}
}
vectormp[maxn];//用vector建立邻接表
void Spfa(int s) {
queuev;
vis[s] = 1; v.push(s); dis[s] = 0;
while (!v.empty()) {
int q = v.front();
v.pop(); vis[q] = 0;
for (int i = 0; i < mp[q].size(); i++) {
if (dis[mp[q][i].s1] > dis[q] + mp[q][i].side) {
dis[mp[q][i].s1] = dis[q] + mp[q][i].side;//更新最短路径。
if (vis[mp[q][i].s1]) {
continue;//如果已经标记，则继续下一次循环
}
v.push(mp[q][i].s1);
}
}
}
}
int main()
{
int x, y, r;
cin >> n >> m >> s;
init();
while (m--) {
node h;
cin >> x >> y >> r;
h.s1 = y;//因为该图为有向图，记录指向的结点
h.side = r;//记录路径
mp[x].push_back(h);
}
Spfa(s);
for (int i = 1; i <= n; i++) {
cout << dis[i] << " ";
}
}
于是我->
AC了，那SPFA算法就到此结束了，总体来说注意细节，在数据较大时候谨慎使用.
5.总结：
1.DFS，Dijkstra，SPFA主要解决单源最短路径。
2.Floyed时间复杂度较高，但是可以解决多源最短路径。
3.Dijkstra虽然效率比较高，但是无法解决负权值的问题。
4.SPFA在数据较大的时候容易被卡，但更加有利于解决有负边权的情况，以及判断是否有负环。
5.在图论中一定要掌握好邻接表和邻接矩阵的建立。
基础知识充分了解之后，就是形成知识网络练习的过程了，希望阅读该文章后能让自己以及读者在图论方面有更深刻得到理解。图，何止是图！！！