SM4国密算法原理及python代码实现
SM4简介
SM4.0(原名SMS4.0)是中华人民共和国政府采用的一种分组密码标准,由国家密码管理局于2012年3月21日发布。相关标准为“GM/T 0002-2012《SM4分组密码算法》(原SMS4分组密码算法)”。
在商用密码体系中,SM4主要用于数据加密,其算法公开,分组长度与密钥长度均为128bit,加密算法与密钥扩展算法都采用32轮非线性迭代结构,S盒为固定的8比特输入8比特输出。
SM4.0中的指令长度被提升到大于64K(即64×1024)的水平,这是SM 3.0规格(渲染指令长度允许大于512)的128倍。
算法原理
基本构建
输入明文(x0,x1,x2 , x3) 128位,共四个32位字。
输入轮密钥:rki(i=0,1…,31) 共32个32位字轮密钥
输出密文(y0,y1,y2,y3) 128位,四个32位字
算法结构:轮函数32轮迭代,每轮使用一个密钥:
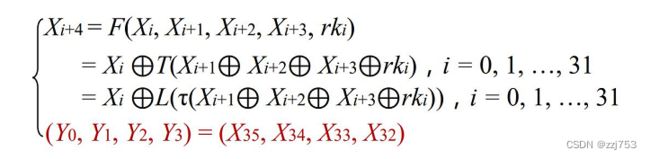
具体运算
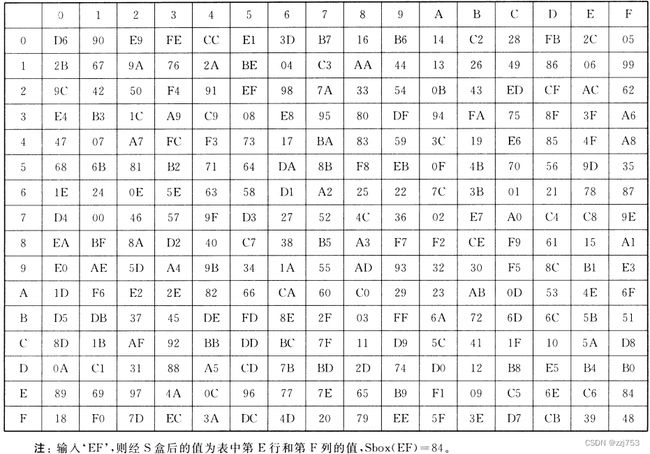
S盒
8输入8输出的密码构建,由前四个比特决定行号,后四个比特决定列号,行号列号确定输出。是唯一的非线性构建。
非线性字变换
相当于四个s盒并置。输入32位字A=(a0,a1,a2,a3),输出B=(b0,b1,b2,b3)。
B=(s-box(a0),s-box(a1),s-box(a2),s-box(a3))

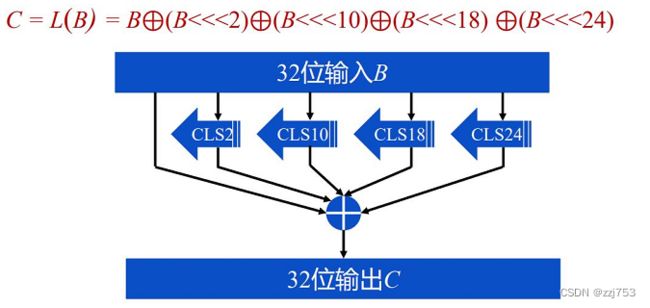
线性L变换
字变换组合与轮函数
字变换组合输入32位,输出32位,即先进行非线性字变换再进行线性L变换。

轮函数:
输入128位字X=(x0,x1,x2,x3),每个xi为32位字。
输入轮密钥:rk,32位字
输出32位字的数据
轮函数运算过程如下:
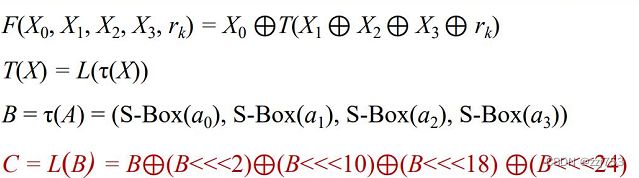
密钥生成
常量参数
SM4密钥扩展算法
输入加密密钥128位MK=(MK0.MK1.MK2.MK3)
输出轮密钥每个32位:rki( i=0,1,2…,31)
中间数据每个32位Ki( i=0,1,2…,35)
算法流程如下:
解密算法
SM4加解密算法是对合的,因此只需要反向使用轮密钥即可解密。

编程实现
这个算法都是基本运算,编程实现难度不大,由于是对合运算所以我只编写了加密部分,话不多说上代码:
sbox = [[0xd6, 0x90, 0xe9, 0xfe, 0xcc, 0xe1, 0x3d, 0xb7, 0x16, 0xb6, 0x14, 0xc2, 0x28, 0xfb, 0x2c, 0x05,],
[0x2b, 0x67, 0x9a, 0x76, 0x2a, 0xbe, 0x04, 0xc3, 0xaa, 0x44, 0x13, 0x26, 0x49, 0x86, 0x06, 0x99,],
[0x9c, 0x42, 0x50, 0xf4, 0x91, 0xef, 0x98, 0x7a, 0x33, 0x54, 0x0b, 0x43, 0xed, 0xcf, 0xac, 0x62,],
[0xe4, 0xb3, 0x1c, 0xa9, 0xc9, 0x08, 0xe8, 0x95, 0x80, 0xdf, 0x94, 0xfa, 0x75, 0x8f, 0x3f, 0xa6,],
[0x47, 0x07, 0xa7, 0xfc, 0xf3, 0x73, 0x17, 0xba, 0x83, 0x59, 0x3c, 0x19, 0xe6, 0x85, 0x4f, 0xa8,],
[0x68, 0x6b, 0x81, 0xb2, 0x71, 0x64, 0xda, 0x8b, 0xf8, 0xeb, 0x0f, 0x4b, 0x70, 0x56, 0x9d, 0x35,],
[0x1e, 0x24, 0x0e, 0x5e, 0x63, 0x58, 0xd1, 0xa2, 0x25, 0x22, 0x7c, 0x3b, 0x01, 0x21, 0x78, 0x87,],
[0xd4, 0x00, 0x46, 0x57, 0x9f, 0xd3, 0x27, 0x52, 0x4c, 0x36, 0x02, 0xe7, 0xa0, 0xc4, 0xc8, 0x9e,],
[0xea, 0xbf, 0x8a, 0xd2, 0x40, 0xc7, 0x38, 0xb5, 0xa3, 0xf7, 0xf2, 0xce, 0xf9, 0x61, 0x15, 0xa1,],
[0xe0, 0xae, 0x5d, 0xa4, 0x9b, 0x34, 0x1a, 0x55, 0xad, 0x93, 0x32, 0x30, 0xf5, 0x8c, 0xb1, 0xe3,],
[0x1d, 0xf6, 0xe2, 0x2e, 0x82, 0x66, 0xca, 0x60, 0xc0, 0x29, 0x23, 0xab, 0x0d, 0x53, 0x4e, 0x6f,],
[0xd5, 0xdb, 0x37, 0x45, 0xde, 0xfd, 0x8e, 0x2f, 0x03, 0xff, 0x6a, 0x72, 0x6d, 0x6c, 0x5b, 0x51,],
[0x8d, 0x1b, 0xaf, 0x92, 0xbb, 0xdd, 0xbc, 0x7f, 0x11, 0xd9, 0x5c, 0x41, 0x1f, 0x10, 0x5a, 0xd8,],
[0x0a, 0xc1, 0x31, 0x88, 0xa5, 0xcd, 0x7b, 0xbd, 0x2d, 0x74, 0xd0, 0x12, 0xb8, 0xe5, 0xb4, 0xb0,],
[0x89, 0x69, 0x97, 0x4a, 0x0c, 0x96, 0x77, 0x7e, 0x65, 0xb9, 0xf1, 0x09, 0xc5, 0x6e, 0xc6, 0x84,],
[0x18, 0xf0, 0x7d, 0xec, 0x3a, 0xdc, 0x4d, 0x20, 0x79, 0xee, 0x5f, 0x3e, 0xd7, 0xcb, 0x39, 0x48]]
FK0=0XA3B1BAC6
FK1=0X56AA3350
FK2=0X677D9197
FK3=0XB27022DC
CK = [0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269, 0x70777e85, 0x8c939aa1, 0xa8afb6bd, 0xc4cbd2d9,
0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249, 0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9,
0xc0c7ced5, 0xdce3eaf1, 0xf8ff060d, 0x141b2229, 0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209, 0x10171e25, 0x2c333a41, 0x484f565d, 0x646b7279]
rk = [0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0,
0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0]
#初始轮密钥全部置零
def xun(X,i):#循环左移
return ((X<<i)& 0xffffffff)|(X>>(32-i))
def s_(x):#s盒 8输入8输出
row = x >> 4
nuw = x & 0xf
return sbox[row][nuw]
def L_(x):#线性L变换 32输入32输出
return x^xun(x,2)^xun(x,10)^xun(x,18)^xun(x,24)
def T_(x):#字变换组合 32输入32输出
a0 = (x >> 24) & 0xff
a1 = (x >> 16) & 0xff
a2 = (x >> 8) & 0xff
a3 = (x >> 0) & 0xff
B = (s_(a0)<<24)^(s_(a1)<<16)^(s_(a2)<<8)^(s_(a3)<<0)#先s盒变换
return L_(B)#再L变换
def T(x):#密钥扩展字变换
a0 = (x >> 24) & 0xff
a1 = (x >> 16) & 0xff
a2 = (x >> 8) & 0xff
a3 = (x >> 0) & 0xff
B = (s_(a0) << 24) ^ (s_(a1) << 16) ^ (s_(a2) << 8) ^ (s_(a3) << 0) # 先s盒变换
return B ^ (xun(B,13)) ^ (xun(B,23))
def K_(MK0,MK1,MK2,MK3):#SM4密钥扩展算法
K = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
K[0] = MK0 ^ FK0
K[1] = MK1 ^ FK1
K[2] = MK2 ^ FK2
K[3] = MK3 ^ FK3
for i in range (32):
rk[i]=K[i+4]=K[i]^T(K[i+1]^K[i+2]^K[i+3]^CK[i])
def SMJ(x):#SM4加密算法
X = [0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0,
0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0, 0x0]
X[0] = (x >> 96) & 0xffffffff
X[1] = (x >> 64) & 0xffffffff
X[2] = (x >> 32) & 0xffffffff
X[3] = (x >> 0) & 0xffffffff
for i in range(33):
X[i+4] = X[i]^T_(X[i+1]^X[i+2]^X[i+3]^rk[i])#轮函数
return (X[35]<<96)^(X[34]<<64)^(X[33]<<32)^X[32]
if __name__ == '__main__':
MK = int(input("请输入加密密钥: "), 16)
MK0=(MK>>96)&0Xffffffff
MK1=(MK>>64)&0Xffffffff
MK2=(MK>>32)&0Xffffffff
MK3=(MK>>0)&0Xffffffff
K_(MK0, MK1, MK2, MK3)
x = int(input("请输入明文: "), 16)
print("密文为:{:x}".format(SMJ(x)))