Learning C++ No.17【STL No.7】双端队列

引言：

北京时间：2023/3/17/7:18，刚刚快乐的早锻炼回来（不对 ，应该说回来有一会了），因为此时我已经吃完早饭，洗过澡了；现在回想起上学期，就算是第二天需要晨跑（6点起床），但我依然毫不畏惧，博客没写完，或者视屏没看完，我都会硬刚（有时到凌晨2-3点），但大部分时间都是硬刚都1点左右，然后写完博客（顺带会发个朋友圈，哈哈哈！（浏览量）），然后快乐的去睡觉， 然后就算6点起床，也不怎么当回事（但是这样是不好滴），长逗严重，所以当时我对这个早锻炼活动可以说是万般的厌恶（认为，这种活动结束后，大家不都是直接回到宿舍，然后继续睡吗？这不是影响我们的作息吗？有什么意义呢？），但是现在，我发现我的看法改变了（猜我现在在干嘛！），你答对了，我现在在码字，哈哈哈！所以现在的我，再也不熬夜了，每天准时在时间范围内睡觉，早起虽然依旧难受，但是，活动完之后，我发现，我多了一个早上的时间（7点-10点）进行码字，只是把写博客、看视屏的时间给调整了一下而已（主要不长逗），开心！虽然此时我觉得这个活动还是那么不聪明的样子，但是起码不厌恶了，所以我明白了一个道理（可能以前明白过），可能只是没有那么深，就是当我们无法改变环境的时候，我们只能去适应环境，通过体验，调整出一个更适合自己生存的环境，俗话说的好，识时务者为俊杰！所以适应环境真的非常重要（不要逆天改命哦！小伙伴们），OK！充分意识到引言写太长了，但是没关系，管他那么多呢？上天安排的最大嘛！（曾经有一份真诚的爱情放在我面前，我没有珍惜，等我失去的时候才后悔莫及，人世间最痛苦的事莫过于此。 如果上天能够给我一个再来一次的机会，我会对那个女孩子说三个字：我爱你！），哦！，不！，不！，不！紫霞！完蛋，电视看太多了，（也可能是星爷的电视太过于经典），导致一涉及就容易无法自拔，哈哈哈！OK！真的不能搞笑了，这篇博客的引言真的已经要不属于引言的范畴了（爱怎么写怎么写，略略略！），今天我们就继上篇博客中栈和队列的知识，来聊一聊栈和队列的经典适配器，双端队列（deque）和有关优先级队列（priority queue）的知识，当然重点还有一个叫仿函数的东西哦！（STL六大巨头之一，可不是泛泛之辈，尔等岂敢小瞧），目标明确，Here we go ，Here we go ！（看到这句，我总是会联想到有些美剧中的经典枪战场景（不置可否！））

上篇博客我们学习了STL中的两个容器适配器，栈和队列，并且发现，栈和队列的学习成本不高（数据结构和string、vector、list），因为我们已经了解了很多有关知识，所以轻轻松松就把栈和队列的知识给搞定了，并且我们解决了两个经典的有关栈的题目，获取最小栈和栈的弹出，发现有的题目就是为栈这个数据结构设计的，使用栈来解决这种问题非常的合适，所以接下来，我们再来看两个有关栈的经典题目。

1.计算逆波兰表达式

题目：逆波兰表达式
例：我们平时算加减乘除时，把 1+2*3-4叫做是中缀表达式，但是中缀表达式并不可以通过栈的方式（入栈出栈）实现4则运算，所以需要把中缀表达式给转化成后缀表达式，例：1 2 3 * + 4 -（后缀表达式），这样就可以很好的利用栈的输入输出来实现四则远算了，但此时我们先不探讨如何将一个后缀表达式转换成中缀表达式，我们先探讨一下如何使用栈的方式来计算一个后缀表达式（逆波兰表达式）

解题思路：

1. 遇到操作数就入栈 （1 2 3 4 5）
2. 遇到操作符（"+" "-" "*" "/"）就取栈顶和栈顶后一个两个操作数进行运算，运算结果重新入栈
3. 最后栈中的数据就是我们的结果（切记，此时是使用后缀表达式（逆波兰表达式）进行的运算），不存在运算符优先级问题

注意：加和乘由于运算关系不改变，所以没事，但是减和除会出问题，所以在出数据的时候，要把栈顶数据放到运算符的右边，栈顶后一个数据放到左边

代码实现如下：

#include
#include
#include
#include
#include
using namespace std;

class Solution
{
public:
	int evalRPN(vector<string>& tokens)
	{
		stack<int> st;
		for (auto& str : tokens)
		{
			if (str == "+" || str == "-" || str == "*" || str == "/")
			{
				int right = st.top();
				st.pop();
				int left = st.top();
				st.pop();
				switch (str[0])/
				{
				case'+':
					st.push(left + right);
					break;
				case'-':
					st.push(left - right);
					break;
				case'*':
					st.push(left * right);  
					break;
				case'/':
					st.push(left / right);  
					break;
				}
			}
			else
			{
				st.push(stoi(str));
			}
		}
		return st.top();
	}
};

代码细节注意点：

1. 因为题目给给我们的是一个后缀表达式（以字符串的形式），并且因为switch case语句中的case只能针对于整形数据（char属于整形一簇（强转）），所以我们在遍历字符串中的字符数据时，此时就不可以直接用switch接收，所以只能使用if语句进行判断
2. 并且由于减和除运算符的特性，所以要区别左操作数和有操作数
3. 使用stoi函数(string类)，可以直接将一个字符类型的数据转换为整形数据
4. 不要把case语句中的break给漏掉了（case和break是需要匹配使用的，作用就是类似于else if语句）

2.中缀表达式转后缀表达式题目

搞定了上述的这个题目，此时我们就来看一下这个题目的前提，就是如何把一个中缀表达式转换成后缀表达式，当然前提还是在使用栈，通过栈来判断各个运算符的优先级，进而构成后缀表达式

例：将中缀1 + 2 * 3 - 4转换成后缀，1 2 3 * + 4 -

原理：
a. 如果是操作数，就直接存储到字符串数组中（string）
b. 如果是操作符（入栈）但是要分成两种情况：

1. 栈为空（入栈）
2. 栈不为空，（重点），让这个操作符去和栈顶的操作符进行比较，如果这个操作符的优先级高，就将该操作符入栈（不进行运算的原因是，防止还有优先级更高的操作符），但是如果这个操作符的优先级低或者相等，那么此时就要把栈顶的操作符出栈，然后进行运算（原因：该操作符优先级比上一个栈顶中的操作符高，比下一个操作符的优先级也高）那么此时它就是三个操作符中优先级最高的，那么此时出栈，对该运算符进行运算，并且此时栈顶的运算符得到运算之后，该优先级低的操作符需要和下一个操作符继续比较（递归实现），同理，高就入栈，低就出栈顶，然后继续递归比较

代码实现如下：

#include
#include
#include
#include
#include
using namespace std;

bool IsPra(char c) 
{
	return (c == '(' || c == ')') ? true : false;
}
int GetPriority(char c)
{
	switch (c) 
	{
	case '+':
	case '-':
		return 0;   
		break;
	case '*':
	case '/':
		return 1;   
		break;
	case '(':
	case ')':
		return -1;  
		break;
	default:
		cout << "输入其他运算符\n" << endl;
	}
}
void CheckPriority(char c, stack<char>& operator_s, string& suffix) 
{
	if (operator_s.empty()) 
	{
		operator_s.push(c);
		return;
	}

	if (IsPra(c)) {
		if (c == '(') 
		{
			operator_s.push(c);
		}
		else {
			// 弹出所有元素直到遇到左括号
			while (operator_s.top() != '(')
			{
				suffix += operator_s.top();
				operator_s.pop();
			}

			// 遇到左括号，弹出且不加入后缀表达式
			operator_s.pop();
		}
	}
	else {
		// 如果不是括号，比较当前元素，与栈顶元素的优先级
		if (GetPriority(c) > GetPriority(operator_s.top()))
		{
			operator_s.push(c);
		}
		else {
			suffix += operator_s.top();
			operator_s.pop();

			//递归方式循环比较
			check(c, operator_s, suffix);
		}
	}
}
string InfixToSuffix(string& infix) 
{
	stack<char> operator_s; // 运算符栈
	string suffix;          // 后缀表达式

	for (int i = 0; i < infix.size(); ++i) {
		if (infix[i] >= '0' && infix[i] <= '9')
		{
			suffix += infix[i];
		}
		else 
		{
			CheckPriority(infix[i], operator_s, suffix);
		}
	}

	// 对中缀表达式的遍历结束，将栈中元素加入后缀表达式
	while (!operator_s.empty()) {
		suffix += operator_s.top();
		operator_s.pop();
	}

	return suffix;
}

如上代码，分为四个函数实现：

1. 第一个函数bool IsPra(char c) ，判断中缀表达式中是否有括号；
2. 第二个函数int GetPriority(char c)固定运算符的优先级；
3. 第三个函数void CheckPriority(char c, stack& operator_s, string& suffix) 对运算符的优先级进行判断（代码核心实现），也就是进行数据的比较；
4. 第四个函数string InfixToSuffix(string& infix) ，合并操作数和操作符（栈中已经排好序了），此时就得到了我们想要的后缀表达式，可以直接通过栈，实现计算的后缀表达式。

并且注意：

此时解决括号问题的方法有非常的多，如上述代码使用的，将左括号和右括号的优先级都设置成最低，并且在入栈时，不需要进行比较（特殊处理），直接入栈，然后同理，将括号之间的操作符进行比较，最终当右括号(“)”)遇到左括号(“(”)时，将左括号弹出（删除栈顶元素），继续同理往下走；

但是这里也可以使用别的方法，例如：使用一个flag=0，如果遇到括号让flag=1，然后在flag=1的前提下，遇到的下一个运算符的优先级就是最高的（无论加减），等一系列的方法都可以，只要你控制得住；

所以我们的思路是：
()优先级最低
( 特殊处理（不比较直接入栈）
) 参与比较，直到遇到左括号，弹出左括号

总: 中缀转后缀利用栈的目的就是进行运算符的优先级的比较（遍历运算字符串，然后通过栈比较出运算符的优先级），然后通过入栈和出栈，进行操作数和操作符的运算，所以栈的用处在这些题目方面是非常的适用的，我们应该合理使用栈的特性（先进后出）。

浅谈双端队列（deque）

搞定了上述的题目，栈和队列的知识也就告一段落了， 并且在上篇博客中，我们说过栈和队列是使用一个叫deque的容器适配器实现的，所以此时我们就来看一看什么是deque；首先无论是在以前的迷宫题目，还是vector题目，我们都学习过类似二维数组的结构，或者说是vector>的结构，所以在此类型结构之下，我们来学学deque的结构 (list+vector) ，显然是与我刚刚所说的两个结构类似，如下图：

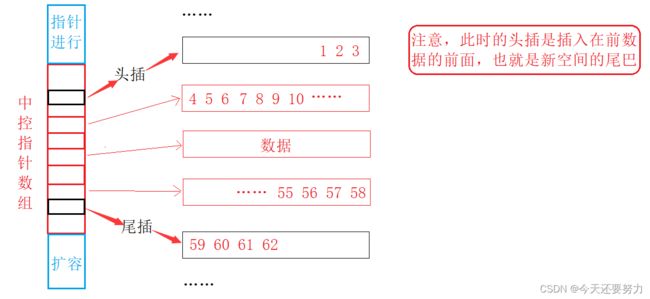
如上图，可以看出，我们是使用了一个指针数组来存放很多的小数组的地址，这样，我们就可以通过控制指针数组中指针指向的地址的空间来控制小数组中的数据了，并且发现，如果存储的数据量非常大，需要扩容，此时就不再需要像vector一样，开辟一个扩容之后的空间，然后把原来空间的数据拷贝，最后将原空间释放掉（目的：防止数据量太大太小）；此时按照上图的结构，就可以直接对指针数组进行扩容，开辟更多的指针出来，消耗对于内置类型来说降低了整数倍，但是对于自定义类型来说就是降低了n倍（例：vector>类型的数据进行扩容）

所以此时我们就来谈谈上述结构的优点和缺点（deque），首先在学习其优缺点之前，我们先来复习一下vector和list的优缺点：

vector的缺点： 1.频繁扩容，消耗高 2. 头插头删效率很低
vector的优点： 1.使用下标支持随机访问 2.CPU的高速缓存效率高（涉及硬件知识）原因：地址连续

list的缺点：不支持随机访问
list的优点：任意位置插入删除效率高

复习了vector和list的优缺点之后，我们就来看一看它们的结合体deque的优缺点：

优点：如果使用vector和list实现了deque的话，此时deque的优点是：相比vector，扩容的代价低（只需要扩容指针就行，指针指向的数组固定）；头插头删，尾插尾删效率都很高（删除头指针指向的数组中的第一个数据就行）；并且也支持随机访问（例：每一个指针数组中的指针指向的是一个100个数据的vector数组，那么此时就以 /100为找行 %100位找列）此时就找到下标位置了（表示第几个指针数组中的指针，中的第几个下标）

缺点：不支持中间插入删除（如果支持中间插入删除缺点就是不支持随机访问） 并且如果要支持中间插入和删除的话，那么此时它的效率是比vector高，但是比list低；功能方面不够极致（没有vector的随机访问，也没有list的插入删除数据）的效率

所以，综上可以发现，deque的优缺点导致它不怎么适合直接用于存储数据，而是适合做一些容器适配器的适配器，例：栈和队列的适配器，这也就是为什么栈和队列的适配器是deque

deque的迭代器

搞定了上述的知识，我们来看一下，deque这个聚集了list和vector优点于一身的家伙，它的迭代器是怎样实现的吧！如下图：

从上图可以看出，deque的迭代器是比较复杂的，使用了4个原生指针，这里各个指针的作用，不多做讲解，感兴趣的同学，点击该链接deque迭代器指针的作用

此时了解了双端队列（deque）和deque的迭代器，下篇博客我们就学习自我实现好吧！

什么是优先级队列

搞定了双端队列的基本结构和优缺点，此时我们再来学习一下另一个队列，优先级队列，如下图：

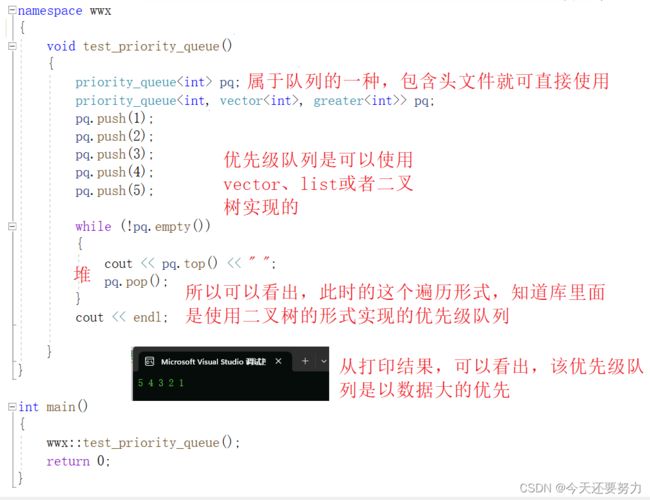
从图中可以发现，优先级队列建的是一个大堆，所以如果我们想要建一个小堆的话，此时就可以引入一个叫仿函数的概念，也就是STL的六巨头之一，greater，具体是什么东西，我们在之后的学习中在深入了解。

浅谈仿函数

template<class T>
struct Less//仿函数
{
	bool operator()(const T& x, const T& y)
	{
		return x < y;
	}
};
template<class T>
struct greater//仿函数
{
	bool operator()(const T& x, const T& y)
	{
		return x > y;
	}
};

int main() 
{
	Less<int> lessFunction;//此时就是让Less这个类的对象可以像是一个函数一样，具有很多的功能（本质上是，去调用了各种的运算符重载，或者是嵌套的函数）
	cout << lessFunction(1, 2) << endl;//此时这句代码的本质是去调用运算符重载，但是看起来像是去调用了一个函数

	return 0;
}

上述的代码就是仿函数greater和less的实现方式，本质上是通过我们的运算符重载实现具体的功能！这里不深入学习，了解即可

总结：STL中还有很多的东西需要我们学习，无论是迭代器还是仿函数，还是map、set容器，还是空间配置器（内存池），任务艰巨！