算法设计与分析 实验四 综合实验

1.平面划分：一条直线可以把平面分成两部分，两条直线分成四部分。那么 n 条直线最多可以把平面分成几部分？

入：多组数据，每组数据一个正整数 1 ≤ n ≤ 1000。

入：3  5    出：7    16

#include
#include
#include
#include
using namespace std;
int main(){
	int n,sum;
	while(cin>>n){
		sum=n*(n+1)/2+1;
		cout<

2.众数问题：给定含有n个元素的多重集合S，每个元素在S中出现的次数称为该元素的重数。多重集S中重数最大的元素称为众数。例如，S={1，2，2，2，3，5}。多重集S的众数是2，其重数为3。对于给定的由n 个自然数组成的多重集S，计算S的众数及其重数。如果出现多个众数，请输出最小的那个。

入：输入数据的第1行是多重集S中元素个数n（n<1300000）；接下来的n行中，每行有一个最多含有5位数字的自然数。

出：输出数据的第1行给出众数，第2行是重数。

入：6 1 2 2 2 3 5    出：2 3

#include
#include
#include
#include
#include
#include 
using namespace std;
void getmax(int &mid,int &m, int a[],int n);
void split(int a[],int n,int &l,int &r);
int main() {
	int n,temp,k; int m=0; int max=0;
	cin>>n;
	int *a=new int[n];
	for(int i=0; i>a[i];
	}
	sort(a,a+n);//数组排序
	int t=0;
	getmax(t ,m, a, n);
	cout< m) {
		m = temp;
		mid = a[t];
	}
	if(l+1 > m) {
		getmax(mid, m, a, l+1);
	}
	if(n-r > m) {
		getmax(mid, m, a+r, n-r);
	}
}
void split(int a[],int n,int &l,int &r) {
	int mid = n/2;
	for(l = 0; l

3.切木棍：有n根长为，a1,a2⋯an​的木棍。对n根木棍总共切k​次（可以在任意点切割），即最后变成n + k根木棍。请输出各种切法得到的n + k​​​​根木棍中最长那根在各种切法中的最短值（答案需要向上取整）。

入：n​ k   出：整数     入： 2 3  7 9   出：4

#include
#include
#include
#include
#include 
using namespace std;
const int MAX=2e5+9;
int ll=0; int rr=2e9+10; int shuzu[MAX];
bool hanshu(int n,int mid,int k);
int main(){
	int n,k,mid;
	while(cin>>n>>k){
		for(int i=0;i>shuzu[i];
		}
		while(ll+1>1;
			bool temp2=hanshu(n,mid,k);
			if(temp2){
				rr=mid;
			}else{
				ll=mid;
			}
		}
		cout<k){
			return false;
		}
	}
	return true;
}

4.二进制数组。有一个数组，里面元素只有0或1，可以删除该数组中的一个元素，然后返回数组中最长连续的1的长度，若不存在，则返回0

入：第一行：数组长度n， 1<=n<=100000 第二行：n个0或1的数字

出：输出一个数字，最长的连续的1的长度

入：6    1 0 1 0 1 1      出：3

#include
#include
#include
#include
#include 
using namespace std;
int main() {
	int n; int cun = 0;  int temp = 0; int left = 0; int right = 0;
	cin>>n;
	int *nums=new int[n];
	for(int i=0;i>nums[i];
	}
	while(right1) {
			temp-=nums[left]== 0? 1 : 0;
			left++;
		}
		right++;
		cun=cun>(right-left-1) ? cun:(right-left-1);
	}
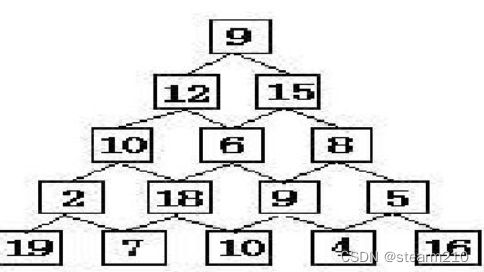
	cout<

5.数字三角形：给出如下图的数字三角形，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

入：输入数据首先包括一个整数T,表示测试实例的个数。

每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度。

接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

入：1  5  7    3 8   8 1 0    2 7 4 4   4 5 2 6 5    出：30

 

#include
#include 
using namespace std;
#define maxsize 110
int main() {
	int n,i,j,t;;
	int a[maxsize][maxsize];int sum[maxsize][maxsize];int id=1;
	cin>>t;
	for(int i=0; i>n) {
			for(i=1; i<=n; i++) {
				for(j=1; j<=i; j++) {
					cin>>a[i][j];
				}
			}
			for(i=1; i<=n; i++) {
				sum[n][i] = a[n][i];
			}
			for(i=n-1; i>=1; i--) {
				for(j=1; j<=i; j++) {
					sum[i][j] = max(sum[i+1][j],sum[i+1][j+1])+a[i][j];
				}
			}
			cout<

6.背包问题：n 种物品，每种物品有重量 w[i]、价值v[i]，数量不限，背包容量为 b。求背包能装物品最大价值。

入：每组数据第一行 n b，表示总共有 n 种物品和背包容量b，其中 1 ≤ n, b ≤ 1000。

接下来 n 行每行两个数 w[i]与v[i] 表示物品的重量与价值，其中 1 ≤ w[i] ≤ b， 1 ≤ v[i] ≤ 1000。

出：输出背包能装的最大价值。

入：4 10   2 1   3 3   4 5   7 9   出：12

#include
#include
#include
#include
#include
#include 
using namespace std;
int w[1020];//重量 int v[1020];//价值 int temp[1020][1020]; //动态规划表
int main() {
	int n,b;
	cin>>n>>b;
	for(int i=1; i<=n; i++) {
		cin>>w[i]>>v[i];
	}
	for (int i = 1; i <=n; i++) {
		for (int j = 1; j <=b; j++) {
			if (j < w[i]) {
				temp[i][j] = temp[i - 1][j];
			} else {
				temp[i][j] = max(temp[i - 1][j], temp[i][j - w[i]] + v[i]);
			}
		}
	}
	cout<

7.不同路径：一个机器人位于一个 m x n 网格的左上角，机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角，问总共有多少条不同的路径？

入：输入一行，包含由空格隔开的两个整数m，n（1<=m，n<=25），表示网格的长宽。

出：输出一行，表示从网格左上角到右下角总共有多少条不同的路径。

入：3  2     出3

#include
#include
#include
#include
#include
#include	
using namespace std;
long long f[110][110];
int main() {
	long long m,n,i,j;
	cin>>m>>n;
    for(i = 0;i < m;i++){
    	f[i][0] = 1;
	}
    for(j = 0;j < n;j++){
    	f[0][j] = 1;
	}
    for(i = 1;i < m;i++){
        for(j = 1;j < n;j++){
            f[i][j] = f[i - 1][j] + f[i][j - 1];
        }
    }
	long long sum=f[m-1][n-1];
	cout<