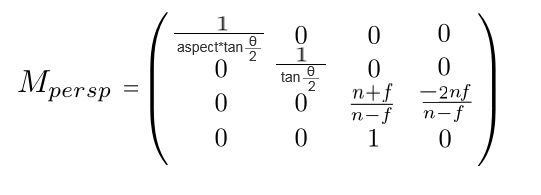计算机图形学(五)-MVP变换之投影(Projection)变换

1 投影变换介绍

之前已经提到MVP变换指的是：模型变换(model)、视图变换(view)、投影变换(projection)。这三大变换好比拍照时的三个步骤：人物摆pose、调整相机、按下快门拍照
投影变换指的就是 “按下快门拍照” 这一步，接下来就说说投影(Projection)变换

投影变换分为正交投影和透视投影

2 正交投影

2.1 正交投影介绍

如上图，正交投影时不管图形与视点的距离是远还是近，图形有多大那么画出来的图形就有多大，正交投影会通过远近裁剪面、前后裁剪面、上下裁剪面六个面确定一个可视空间，在可视空间中的物体才能被看到，被映射在近才截面上

2.2 正交投影矩阵推导

假设有一个大小为[l,r]×[b,t]×[f,n]的立方体，希望它的中心移到坐标原点，并把它变换成标准立方体([-1, 1]³)， 这个过程需要两种变换，平移变换和缩放变换

上图中的立方，l,r表示左边界和右边界，b,t表示下边界和上边界，f,n表示远裁剪面和近裁剪面，这里的远和近需要说明一下，由于相机向-z方向看去，所有离相机越近意味着z值越大，离相机越远z值越小，所以这里的远近和立方体在坐标系中z轴的值的大小正好相反，即值越大距离相机越近，值越小距离相机越远

正交投影矩阵
通过上述变换过程很容易得出正交投影矩阵就是一个缩放矩阵与平移矩阵相乘，具体如下

2.3 正交投影矩阵

合并后最终正交投影矩阵为

3 透视投影

3.1 透视投影介绍

透视投影根据成像原理画出来的图会近大远小，它会出从照相机出发投射出一个视锥空间，在视锥空间中通过近裁剪面和远裁剪面可以裁出一个椎体空间，这个空间称为透视投影的可视空间，确定这个空间有两种方式，一种是把视锥挤压成正射投影通过六个裁剪面确定，另一种是通过视角大小fov和近裁剪面的长宽比aspect来确定

3.2 透视投影矩阵推导

3.2.1 复习齐次坐标

首先要复习一下齐次坐标，后面推导需要用到
如果在齐次坐标系上有一点

(x,y,z,1)

可以给这个点乘以任意一个不等于0的数变为

(kx,ky,kz,k)

既然k是任意不等于零的数，给它乘个z(z!=0)得到

例如在笛卡尔坐标系中有一点(1,2,2)，在其次坐标中可以表示为(1,2,2,1)、(2,4,4,2)、(3,6,6,3)…

3.2.2 透视投影矩阵推导思路

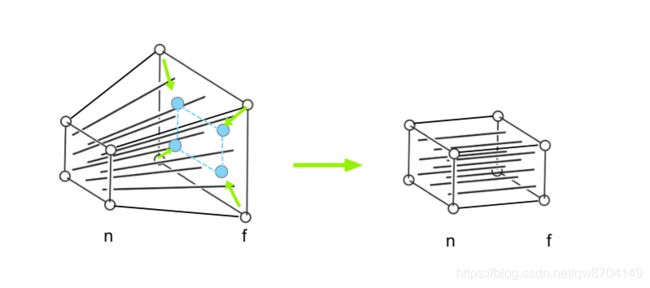
如上图，把透视投影远裁剪面上的四个顶点向内挤压
挤压的过程中要保证

• 近裁剪面不变，
• z值不发生变化，
• 远裁剪面的中心点也不发生变化

挤压成上图右侧的形状，问题就转化为求正交投影矩阵。如此一来可以用下面的方法求透视投影矩阵
透视投影矩阵 = 正交投影矩阵 × 透视投影到正交投影的变换矩阵
即

那么现在只要求出透视投影到正交投影的变换矩阵就可以得到透视投影矩阵

3.2.3 透视投影到正交投影的变换矩阵推导

下图为透视投影模型的侧视图

将点(x,y,z)变换为与点(x’,y’,z’)一样的高度，你会发现图中是两个相似三角形，根据相似三角形的性质，就可以得到

在水平方向上同理可得

根据齐次坐标性质，给每个分量都乘以z，得到远裁剪面上的点与近裁剪面的映射关系

这时有 透视投影到正交投影的变换矩阵 × 远裁剪面上的点 = 挤压后远裁剪面的点

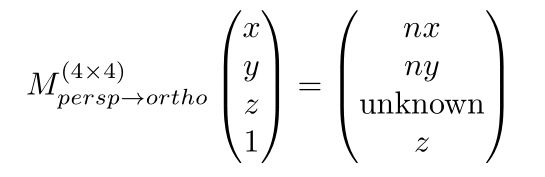
根据矩阵乘法规则，反推得到透视投影到正交投影的变换矩阵，只有第三行还不知道

根据挤压过程的特性 近裁剪面上所有点不发生变化，对远近裁剪面映射关系做如下处理

整理上述操作得

根据矩阵乘法反推，透视投影到正交投影的变换矩阵的第三行的第一列和第二列只能等于0，剩下的第三列和第四列命名为A和B

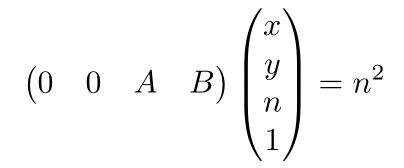
继而得到

根据挤压过程的特性 远裁剪面上z值不发生变化 得到

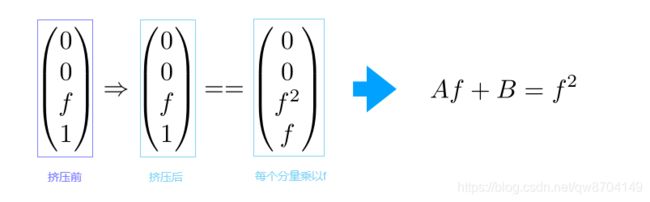
将上面得到的关系表达式，整理计算得到A和B的值

至此，终于得到 透视投影到正交投影的变换矩阵

3.3 透视投影矩阵

3.4 视场角和宽高比表示透视投影矩阵

在视锥中取近裁剪面的上边缘中点和下边缘中点，从相机开始分别连接这两个点，这两条线形成的夹角(上图中红色虚线部分)称为垂直方向视角

下图为视锥的侧视图

通过上图和视锥图我们可以得到

r + l = 0
r - l = 2
t + b = 0
t - b = 2

将上述关系带入 透视投影矩阵 得

假设 视场角度fovY = θ，则有

将 r 和 n 的值带入前一步得到的矩阵，矩阵中分子分别消除掉 n 得到使用视场角和宽高比表示的透视投影矩阵