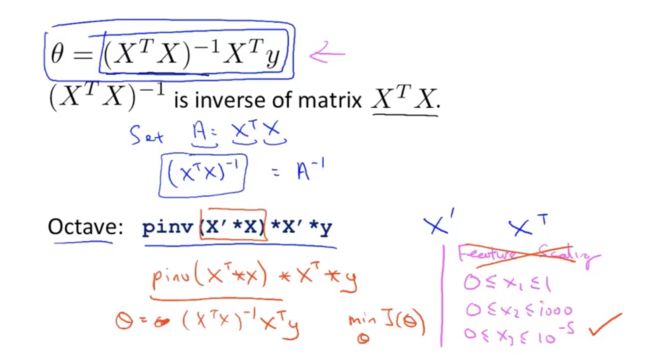P4 【机器学习】多元梯度下降、特征选择、正规方程

目录

1.多变量

2.利用梯度下降处理多元线性回归函数，得到假设参数

3.特征选择和多项式回归 

4.正规方程（区别于迭代方法的直接解法，求得θ的最优值）

4.1 正规方程介绍

​4.2 梯度下降与正规方程比较优缺点

---

1.多变量

利用矩阵书写假设函数 ：

2.利用梯度下降处理多元线性回归函数，得到假设参数

        将假设参数θ不看做分开的独立参数，而是看做一个n维的单位向量。

        如下图，我们的目的是将多元线性函数转移到梯度下降函数中，不断更新θ_j的值，j变一次θ_就随之变一次。

         下图中左边是旧的算法，只有一个变量，右边是多个变量的情况，接下来将会解释为什么这两个算法原理是一样的，他们是相似的算法，以及我们该怎么样进行运用。

下图中右下角解释了更新θ_j的规则，每一行其实都是单个变量的更新规则。 

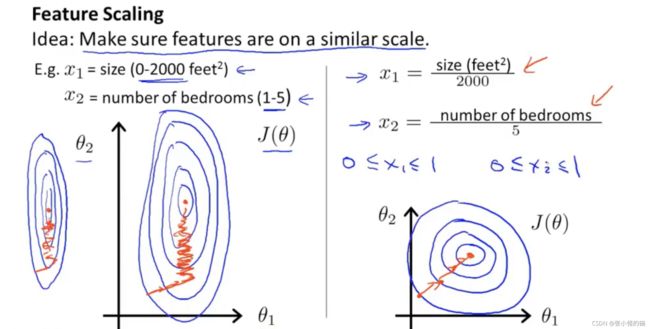
        使用特征缩放的方法使得梯度下降算法能够更快收敛：

        如下图，左边变量x_1和x_2的范围差异很大，会导致梯度下降的速度缓慢，下降路径非常曲折；右边进行特征缩放后，将x_1和x_2的范围都控制在0～1，得到更直接的梯度下降路径。

        依据经验，一般梯度下降的范围控制在[-1,1]会比较好：

特征缩放，不需要太精确，只是为了让梯度下降更快而已。

        如下图特征缩放的另一种方式是将范围控制在0附近，那么就需要在分子用x减去x的平均值，分母是x的范围，用范围最大值减去最小值。

 观察算法是否收敛，左边是直观地用图像来说明，右边是一个自动检测是否收敛的算法。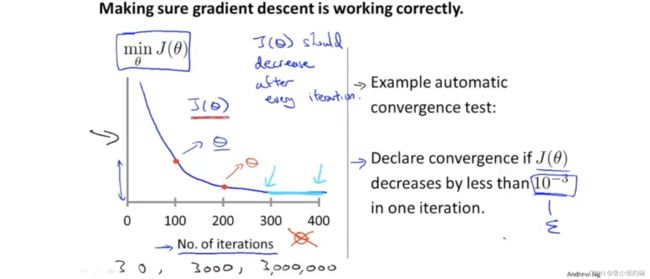

        那么我们怎么样才能保证梯度下降算法正常运行呢？

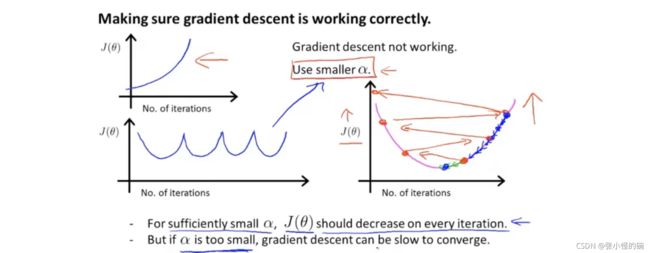
        如下图左半部分的两张图，以迭代次数为横轴，代价函数值为纵轴，我们可能会遇到这两种梯度下降算法不好的情况，都是函数没有收敛的情况。在这两种情况下，比较好的选择都是use smaller ，即使用更小的学习率 。

        在选择 大小时，不可以过大也不可以过小。

        如果 过小，梯度下降的速度会非常慢；如果 过大，在迭代过程中会哦不断越过最低值的函数点，反复横跳，最终无法收敛。

        吴恩达建议的  大小是根据10倍进行分割，选取0.3，0.003等数字。

3.特征选择和多项式回归 

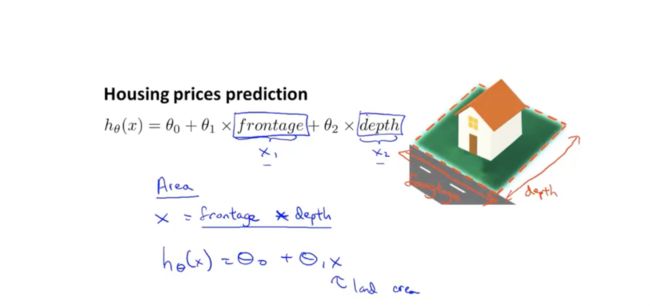
        这一节讨论的是多项式回归，首先拿房价预测举例：下图中的变量可以设置成frontage和depth两个变量，也可以直接是房子的占地面积area，取决于你选取什么变量。

        

特征缩放的重要性体现：

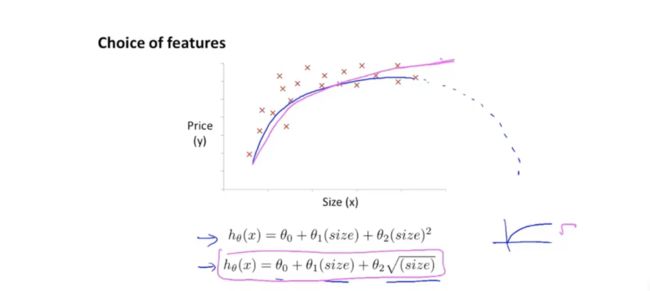
        在下图房价预测的例子中，我们发现蓝色公式是一个二次公式，我们最终得到的曲线可能最后会对着size的增大而price减小，因此我们需要换成绿色的公式，也就是一个三次多元公式，那么图形尾巴会逐渐向上翘起。

        列出假设函数h_θ(x)，我们发现这时一次、二次、三次参数的值的量级从10^3-10^9，如果不进行特征缩放，那么这三个参数就会不具有可比性。 

        其他特征函数举例：（根号次项） 

        在这一节我们学习了如何选择特征，以及选择不同的函数拟合到数据上，之后我们会学到如何确定我们到底应该使用哪些特征，到底选择怎样的函数。

4.正规方程（区别于迭代方法的直接解法，求得θ的最优值）

        之前我们一直使用的线性回归方法是梯度下降法，通过梯度下降的多次迭代来收敛到全局最小值。 现在我们可以使用正规方程一步得到最优解。

4.1 正规方程介绍

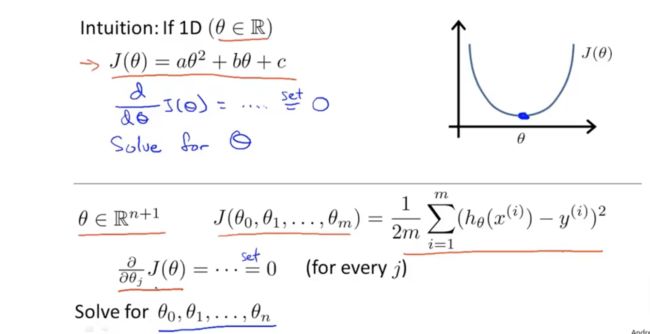
        当θ是实数时，我们通常使用的求解最优解的方法是对二次函数进行求导然后令导数为0得到最小值，但如果θ是一个多维向量，那么这个时候如果仍旧使用上述方法，也可以用微积分对每个维度的θ进行求偏导的操作然后逐个为0求解，但事实上这样做的结果可能会很复杂。

        接下来介绍的方法不是遍历，而是告诉你用什么方法可以掌握方法的原理。

 

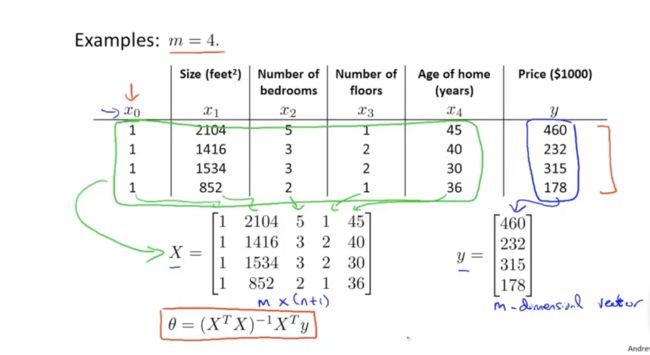
构建矩阵的方法：

 

                 得到 (X^T*X)^(-1)*X^T*Y 求逆公式，可以得到θ的值。 

4.2 梯度下降与正规方程比较优缺点

         如下图所示，前两条是梯度下降的缺点和正规方程的优点：

1.正规方程不需要选择学习率但梯度下降需要

2.正规方程不需要迭代而梯度下降需要

        梯度下降的优点和正规方程的缺点：       

1.梯度下降不需要求解正规方程的求逆函数

2.梯度下降在n（特征数量）很大的时候也能正常运行，但是正规方程会变慢 

        在之后的学习中我们会发现很多算法都用不了正规方程解法，梯度下降法非常有用。