KMP算法实现（绝对通俗易懂）

KMP算法实现（绝对通俗易懂）

博主是一个跨软件专业的学生，在学习KMP算法这里是遇到了很多的麻烦，主要集中在next数组这里。
为什么要用到next数组，怎么求next数组以及怎么用next数组…… 关于这些问题博主会给大家带来一些自己的心得。
KMP的概念是：利用匹配失败的信息尽量减少模式串与主串的匹配次数，从而达到快速 匹配的过程。因此，在具体了解KMP算法之前我们先熟悉一下简单的模式匹配算法（俗称BF模式匹配）
一 ：BF算法：将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果，假设给出在主串S设置指示器i表示S中当前的比较字符，模式串T中设置指示器j表示模式串T中当前的比较字符；
给出： 主串S=a c a b a a b a a b c a c a c a a b c
模式串T=a b a a b c

进行第一趟比较

进行第二趟比较

进行第三趟比较
……诸如此类主串从下一次字符串开始，模式串从第一个字符开始比较，效率很低
思想：从主串第pos个字符起和模式串第一个字符比较
若相等：继续逐个比较后续字符；（i++；j++）
若不相等：从主串下一个字符串和模式串第一个字符进行比较；（i=i-j+2；j=1）

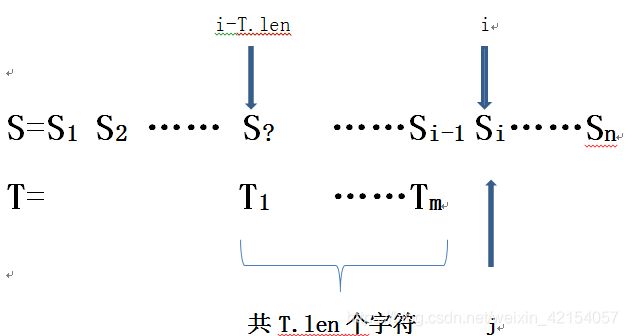
和T1比较的是Si-j+1；若不匹配，不存在位置Si-j+1；下一次比较从Si-j+2位置开始，模式串第一个位置开始逐个比较。
匹配成功：返回模式串中第一个字符相对应主串的序号（return i-T.len）
匹配不成功：返回0（return 0）

现在贴出来代码如下：

int Index (SString S,int pos,SString T)
{
  int i=pos,j=1;
  while(i<=S.len&&i<=T.len)
  {
    if(S.ch[i]==T.ch[j])
    {
      ++i;
      ++j;
    }
    else
    {
      i=i-j+2;
      j=1;
    }
  }
if(j

二：现在说一下KMP算法

KMP算法 ：匹配过程中，不需要回溯主串指针i，时间复杂度达到O(m+n)
解决KMP算法主要是解决next值，接下来介绍两种自己总结的next值的计算方法

---

首先介绍第一种计算方法，可以叫“前后缀法”
给出模式串‘abaabcac’
1 第一位的next值为0
2 第二位的next值为1
后面求解每一位的next值时，根据前一位进行比较
3 第三位的next值：当 j=3时，真前缀‘a’ 真后缀‘b’，不等；则next值为1
4 第四位的next值：当j=4时，真前缀‘ab’ ‘a’，真后缀‘ba’ ‘a’，我们发现真前缀和真后缀的交集是‘a’，长度为1，则next值为1+1=2
5 第五位的next值：当j=5时，真前缀‘aba’ ‘ab’ ‘a’，真后缀‘baa’ ‘aa’ ‘a’，真前缀和真后缀交集是‘a’，长度为1，则next值为1+1=2
6 第六位的next值：当j=6时，真前缀‘abaa’ ‘aba’ ‘ab’，真后缀‘ab’ ‘aab’ ‘baab’，真前缀和真后缀的交集是‘ab’，长度为2，则next值为1+2=3
7第七位的next值：当j=7是，真前缀‘abaab’ ‘abaa’ ‘aba’ ‘ab’ ‘a’，真后缀‘baabc’ ‘aabc’ ‘abc’ ‘bc’ ‘c’，真前缀和真后缀无交集，则next值为1
8第八位的next值：当j=8时，真前缀‘abaabc’ ‘abaab’ ‘abaa’ ‘aba’ ‘ab’ ‘a’，真后缀‘baabca’ ‘aabca’ ‘abca’ ‘bca’ ‘ca’ ‘a’，真前缀和真后缀交集为‘a’，长度为1，则next值为1+1=2

---

介绍第二种next值的计算方法（公式法）

（这里会有人对‘k’和‘ k’ ’有疑问，这个我先不用 文字解释，根据下面的例子解释一下，因为打字解释颇为麻烦）

同样举出上面的例子

1 同样next[1]=0
2 next[2]=1
3我们求next[3]，看第二位的模式串为b，对应next值为1，则将第二位的b与第一位的a进行比较，不等，则next[3]=1（此处第二位的b就是上面公式中Tj，第一位的a则是Tk，我们可以看出来Tk!=Tj，Tk之前不再存在其他字符串，也就是不存在Tk’）
4求next[4]，根据上面解释，Tj对应的字符串为a，next值为1，则Tk为字符串为a，发现Tk=Tj为a，所以根据公式next[4]=next[3]+1=1+1=2
5求next[5]，同理，Tj对应的字符串为a，对应next值为2，则Tk对应的字符串为b，发现Tk!=Tj，则进行公式的下一步，b对应的next值为1，则 k’对应的字符串为a，Tj=Tk’，根据公式，所以next[j+1]=1+1=2
6求next[6]，同理，Tj对应的字符串为b，对应的next值为2，则Tk对应的为2号位置的字符串为b，Tk=Tj，则next[6]=next[5]+1=2+1=3
7求next[7]，Tj对应的是6号位置的字符串c，则Tk对应的是3号位置的字符串a，发现Tk!=Tj，则k’对应的为1号位置字符串a，满足（1 Tk！=Tj ，2 Tj！=Tk’ ），所以不存在k’，即next[7]=1
8 求next[8]，Tj对应的是7号位置的字符串a，Tk对应的是1号位置的字符串a，发现Tk=Tj，则next[8]=next[7]+1=2

---

通过上面的两种方法，我们可以轻松的得到next值的计算方法，接下来展示具体到应用中应该怎么用。
让我们回到问题

发现不匹配，现在查阅next表，发现next[2]=1，则主串不发生改变，将模式串的第一个字符串对应i=2位置，如下图

发现i=2，j=1时发生失配，查阅next表，next[1]=0，则表明首字符发生失配，则i从3号 位置开始，j继续从1号位置进行比较，如下图

此时发现当i=8，j=6时，发生失配，查阅next表，发现next[6]=3，则主串i位置不发生改变，模式串j=3位置对应i=8位置，如下图

此时发现匹配成功，到此表示匹配结束，下面将贴出来代码
next函数值的代码：

void Get_Next(SString T,int next[])
{
    i=j=1,k=0;
    next[1]=0;//next[1]=0是根据定义设置
    while(j

KMP算法代码：

int Index_KMP(SString S,int pos,SString T)
{
    int i=pos,j=1;
    while(i<=S.len&&j<=T.len)
    {
        if(j==0||S.ch[i]==T.ch[j])
        {
            ++i;
            ++j;
        }
        else
            j=next[j];
    }
    if(j>T.len)
        return i-T.len;
    else
        return 0;
}

在此解释一下为何返回i-T.len，如下图

到此next值的计算已经KMP算法的实现完成

---

在此再引入一个nextval函数以及用法
若给出特殊情况

首先我们可以轻松计算出模式串next值

第一趟比较

发现在i=4，j=4时，发生失配，查阅next表，发现next[4]=3,

第二趟比较

i=4，j=3时，发生失配，查阅next表，next[3]=2

第三趟比较

i=4，j=2时，发生失配，查阅next表，next[2]=1

第四趟比较

i=4，j=1时，失配，查阅next表，next[1]=0

以上过程显然未匹配到结果 S4->T4,S4->T3,S4->T2,S4->T1，对T来说，T4,T3,T2,T1的对应字符都是a，从第一次发现S4!=T4，则后面三趟比较也不可能相等，这样有可能将模式串滑动更远距离，因此遇到类似的情况，应对next值进行修改。
引入一个新的概念，当Si和Tj比较之后，发现两者不相等，但Tj和Tk相等，所以Si和Tk不再进行额外的比较，因此j位置的nextvai值修改为k位置的nextval值
若Si和Tj比较之后，发现两者不相等，但Tj和Tk也不相等，那是否必须 比较Si和 Tk呢？因此j位置的nextval值仍然为k。即nextval[j]=next[j],k=next[j],如果T.ch[j]==T.ch[k],则nextval[j]=nextval[k],否则nextval[j]=next[j]。
接下来看具体操作：

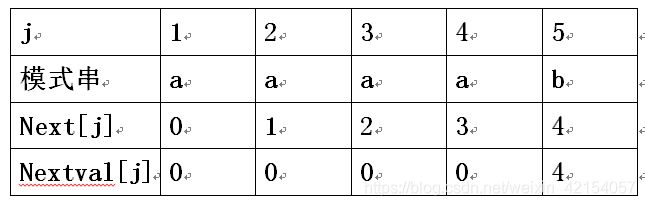
说明一下nextval具体计算过程
1 当j=2时，next[2]=1,T.ch[2]==T.ch[1]为a，所以nextval[2]=nextval[1]=0
2 当j=3时，next[3]=2,T.ch[3]==T.ch[2]为a，所以nextval[3]=nextval[2]=0
3 当j=4时，next[4]=3,T.ch[4]==T.ch[3]为a，所以nextval[4]=nextval[3]=0
4 当j=5时，next[5]=4,T.ch[5]!=T.ch[4],则nextval[5]=next[5]=4

已知nextval情况下，回顾一下上面的问题
第一趟比较

发现i=4，j=4时失配，查表，nextval[4]=0

第二趟比较

发现i=8，j=4时失配，查表，nextval[4]=0

第三趟比较

发现i=12，j=4时失配，查表，nextval[4]=0

第四趟比较

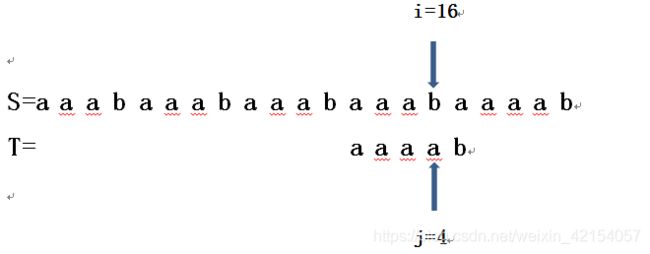
发现i=16，j=4时发生失配，查表nextval[4]=0

进行 第五趟比较

此时发现匹配完成，则返回i=16即可。
发现基于nextval的匹配比基于模式串next的匹配更加高效。
下面贴出来代码：

void Get_Nextval(SString T,int next[],int nextval[])
{
    int j=2,k=0;
    Get_Next(T,next);
    nextval[1]=0;
    while(j<=T.len)
    {
        k=next[j];
        if(T.ch[j]==T.ch[k])
            nextval[j]=next[k];
        else
            nextval[j]=next[j];
            j++;
    }
}

---

到此关于BF算法和KMP算法具体过程已经介绍完毕，小博是一个跨专业考软件的学生，分享一下自己学习过程中的心得和经验，如有错误，恳请大家斧正，以后学习过程中小博会继续分享其他算法的经验和心得，谢谢大家~