正运动学建模方法

【前言】
回顾前面，通过二连杆引入了机器人建模一些内容，其中包括机器人正运动的建模、机器人逆运动学建模、机器人动力学建模，以及涉及一点机器人控制的方法。大体了解了机器人领域需要的知识。详细的内容还需根据相关书籍进一步丰富。重回机器人正运动学，本篇的主要目的在于掌握机器正运动学的建模方法。
【正运动学】
以平面二自由度机械臂为例，正运动学的目的在于：在已知机械臂的关节变量θ1、θ2的情况下，求解机械臂末端的位姿。涉及目标的位姿，需要考虑的目标坐标系的建立（毕竟姿态和位置是相对坐标系而言）；而坐标系的建立可以任意选择，每个人建立坐标系的方式不同，将不利于行业人员的交流。因此，为了解决这个问题，业内制定了一套约定----Denavit-Hartenberg约定。
1.1 Denavit-Hartenberg约定
简称DH约定，用于正运动的分析；其主要的约束条件有：
（DH1）坐标轴xi垂直于坐标轴zi-1；
（DH2）坐标轴xi与坐标轴zi-1相交；
通过这两条约定，存在唯一的a、d、θ、α使得相邻的坐标齐次变换矩阵可以表示为：
A=Rot(θ)Trans(d)Trans(a)Rot(α)
关于这四个变量以下图为例，有以下定义：

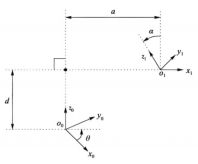
图1满足DH1与DH2约定的坐标系
a-----表示连杆长度，z0与z1之间沿公共法线x1测得得距离；
α----表示连杆扭曲，一个关节轴相对另一个关节轴绕公共法线旋转的角度；
d----表示连杆偏置，O1到x1与z0交点的距离；
θ-----表示关节角度，垂直于Z0平面内x0与x1的角度
1.2 建模实例
（1）DH约定建模
根据DH约定，对以下平面肘型机械臂进行正运动学建模。

第一步：编号
需注意坐标系、杆和关节变量的下标的编号：
a.坐标系从0开始编号，O0,O1,…On,其中O0为基坐标系;
b.关节变量从1开始编号，θ1,θ2,…θn+1;
c.杆从1开始编号，L1,L2,…Ln+1;
第二步：根据以上绘制DH表
第三步：写出齐次变换矩阵；
第四步：根据链式法则写出齐次变换矩阵(4*4)；
第五步：根据变换矩阵写出杆件各连接点的坐标；

clc;clear;
close all;
global ulink;
%定义机械臂参数
ulink.l1=5;
ulink.l2=5;
ulink.sida1 = 45/180*pi;
ulink.sida2 = 90/180*pi;
%----------------------------------------------
%       | a_i   | alfa_i  |  d_i  |  sida_i
%   1   |   l1  |  0      |   0   |   sida1
%   2   |   l2  |  0      |   0   |   sida2
%--------------------------------------------
%DH约定：xi与zi-1相交且垂直
%DH齐次变换矩阵
% Ai =
%         [ cos(sida_i), -cos(alfa_i)*sin(sida_i),  sin(alfa_i)*sin(sida_i), a_i*cos(sida_i)]
%         [ sin(sida_i),  cos(alfa_i)*cos(sida_i), -sin(alfa_i)*cos(sida_i), a_i*sin(sida_i)]
%         [           0,              sin(alfa_i),              cos(alfa_i),             d_i]
%         [           0,                        0,                        0,               1]
syms sida_i alfa_i a_i d_i
%计算齐次矩阵
sida_i = ulink.sida1;
alfa_i = 0;
d_i =0;
a_i = ulink.l1;
A0_1 = [cos(sida_i)  -sin(sida_i)*cos(alfa_i)    sin(sida_i)*sin(alfa_i)   a_i*cos(sida_i);
        sin(sida_i)   cos(sida_i)*cos(alfa_i)   -cos(sida_i)*sin(alfa_i)  a_i*sin(sida_i) ;
            0         sin(alfa_i)                cos(alfa_i)                    d_i       ;
            0                 0                       0                          1             
    ];
sida_i = ulink.sida2;
alfa_i = 0;
d_i =0;
a_i = ulink.l2;
A1_2 = [cos(sida_i)  -sin(sida_i)*cos(alfa_i)    sin(sida_i)*sin(alfa_i)   a_i*cos(sida_i);
        sin(sida_i)   cos(sida_i)*cos(alfa_i)   -cos(sida_i)*sin(alfa_i)  a_i*sin(sida_i) ;
            0         sin(alfa_i)                cos(alfa_i)                    d_i       ;
            0                 0                       0                          1             
    ];
A0_2 = A0_1*A1_2;
%绘图 plot([x1,x2],[y1,y2],'k')
figure(1)
plot([0,A0_1(1,4)],[0,A0_1(2,4)],'k','Linewidth',5)
axis equal
hold on
plot([A0_1(1,4),A0_2(1,4)],[A0_1(2,4),A0_2(2,4)],'r','Linewidth',5)  

（2）向量法建模
第一步：编号，参考DH建模；
第二步：对基坐标的各坐标轴用单位向量表示（正交）；
第三步：依次写出Oi坐标系各轴在Oi-1坐标系的表示；
第四步：根据链式法则写出旋转变换矩阵(3*3)；
第五步：将各杆用向量表示；

clc;clear;
close all;
global ulink;
%定义机械臂参数
ulink.l1=5;
ulink.l2=5;
ulink.sida1 = 45/180*pi;
ulink.sida2 = 90/180*pi;
%向量法
%定义世界坐标系Oo
x0=[1,0,0]';
y0=[0,1,0]';
z0=[0,0,1]';
%定义局部坐标系O1(相对O0而言)
x1=x0*cos(ulink.sida1)+y0*sin(ulink.sida1);
y1=-x0*sin(ulink.sida1)+y0*cos(ulink.sida1);
z1=z0;
%定义局部坐标系O2(相对O1而言)
x2=x0*cos(ulink.sida1)+y0*sin(ulink.sida1);
y2=-x0*sin(ulink.sida1)+y0*cos(ulink.sida1);
z2=z0;
%写出齐次变换矩阵
R0_1 = [x1,y1,z1];
R1_2 = [x2,y2,z2];
R0_2 = A0_1*A1_2;
O0_1=ulink.l1*R0_1(:,1);
O0_2=O0_1+ulink.l2*R0_2(:,1)
%绘图
figure(1)
plot([0,A0_1(1,4)],[0,A0_1(2,4)],'k','Linewidth',5)
axis equal
hold on
plot([A0_1(1,4),A0_2(1,4)],[A0_1(2,4),A0_2(2,4)],'r','Linewidth',5)  

前期内容代码已更新至公众号