区间DP模型与题目详解acm
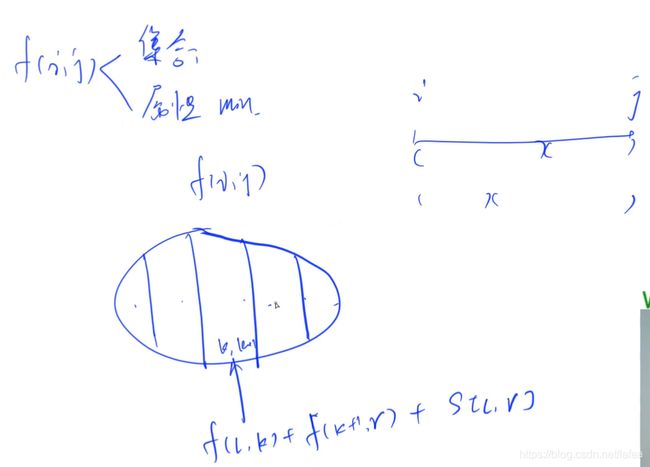
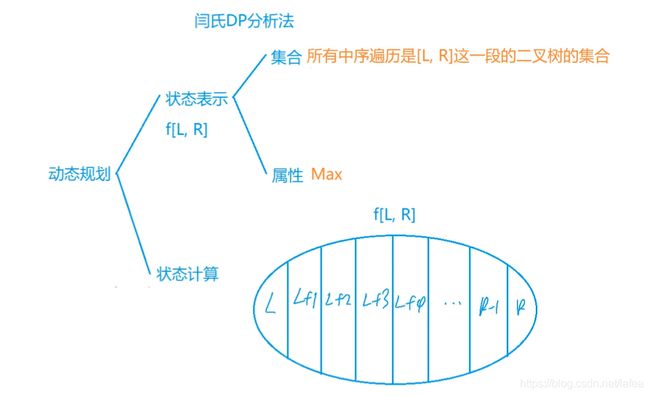
区间DP问题
- #写在前面
-
- ##石头合并
-
- ----c++版
- ##环形石头合并
-
- ----c++版
- ##能量项链
-
- ----c++版
- ##凸多边形的划分
-
- ----c++版
- ##加分二叉树
-
- ----c++版
- ##棋盘分割
-
- ----c++版
#写在前面
##石头合并
https://www.acwing.com/problem/content/284/
----c++版
#include##环形石头合并
https://www.acwing.com/problem/content/1070/
具体思路:
如何转化成上一个问题来做?
上一题是给定一个区间,我们都可以求出区间内石子合并的最小代价
如何把环转化为区间?

环上每两个点连一条边,表示其可以合并,我们最多合并n-1次,所以n个点的环上最多会连n-1条边,
也就是最终会有一个缺口
将这个缺口展开,可以得到一条链
只需对这条链进行上题的石子合并即可
以缺口为分界点,枚举每个缺口,可以得到n条链
问题转化为对n条链分别做石子合并
上题的时间复杂度是n^3,
枚举缺口有n^4的复杂度,n=200时有8亿,会超时
这里有一种普遍的优化方式
我们本质上要求n条长度为n的链上的石子合并问题
我们把链复制一遍接到后边即可

再在所有长度是n的区间 f [ i, i+n-1 ] 中取最值即可
(2n)^3 ,n=200时有64000000,不会超时
----c++版
#include##能量项链
https://www.acwing.com/problem/content/322/
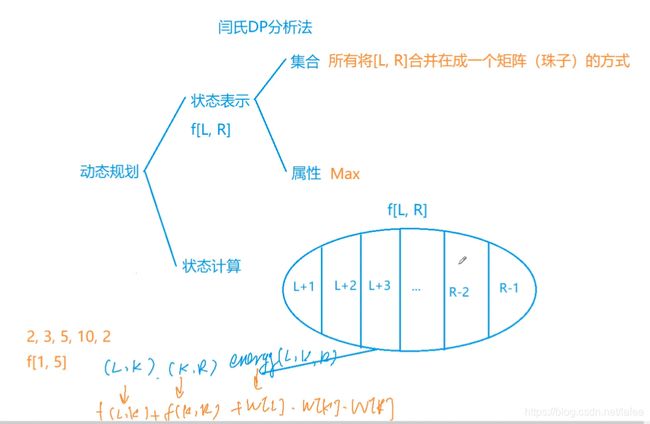
有点像矩阵乘法

链式的区间dp
集合还是以分界线的形式划分
线性做法:
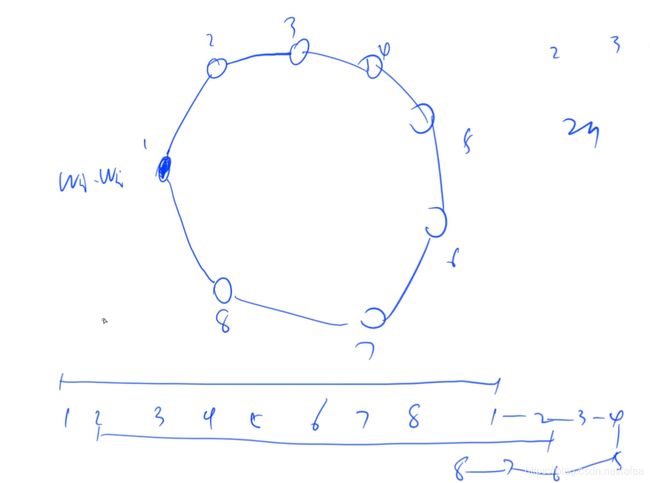
环形做法:
这题是把一个珠子断开,首位有相同的珠子
有n个珠子,有n种断开方式
和上一题差不多
----c++版
#include##凸多边形的划分
https://www.acwing.com/problem/content/1071/
这题和上一题的状态转移方程完全一样
可以发现三角形的左右两边是独立的,也就是这个三角形将多边形划分成了3个部分,每个部分取最值
这题要写个高精度
一般先写不是高精度的过掉样例,再写成高精度的
----c++版
无高精度
#include偷懒数组模拟高精度
#include##加分二叉树
区间dp问题记录方案
https://www.acwing.com/problem/content/481/
----c++版
#include##棋盘分割
https://www.acwing.com/problem/content/323/
----c++版
#include