【题解】2023牛客寒假算法基础集训营4
目录
- A 清楚姐姐学信息论
-
- 思路
- B. 清楚姐姐学构造
-
- 思路
- C. 清楚姐姐学01背包(Easy Version)
-
- 思路
- D. 清楚姐姐学01背包(Hard Version)
-
- 思路
- E. 清楚姐姐打怪升级
-
- 思路
- F. 清楚姐姐学树状数组
-
- 思路
- G. 清楚姐姐逛街(Easy Version)
-
- 思路
- L. 清楚姐姐的三角形I
-
- 思路
- M. 清楚姐姐的三角形II
-
- 思路
A 清楚姐姐学信息论
思路
tag:签到
进制是效率最高的进制,越靠近e进制效率越高。
证明如下:
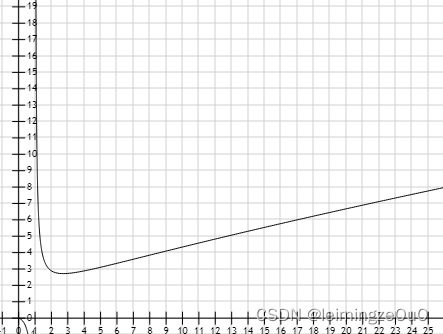
如果有一个n位r进制数,则表示这个数一共需要n*r张牌
(成本),一共可以表示r^n个数(回报),那么关于成本的式子
即:r*log(r,m)
m是常量,对r/lnr求导,发现其在x=e为极值点,则直接输出。
int x,y;
void solve()
{
cin>>x>>y;
if(x>y)swap(x,y);
if(x==2&&y==3)cout<<3<<endl;
else cout<<min(x,y)<<endl;
}
B. 清楚姐姐学构造
思路
tag 数学,构造
构造 a i = a j a_i=a_j ai=aj, b i = − b j b_i=-b_j bi=−bj。
由题可知 a i + b i ≡ c i a_i+b_i\equiv c_i ai+bi≡ci, a j + b j ≡ c j a_j+b_j\equiv c_j aj+bj≡cj。
则 2 a i ≡ c i + c j 2a_i\equiv c_i+c_j 2ai≡ci+cj
分情况讨论:
- 如果 c i + c j c_i+c_j ci+cj为偶数,则直接赋值 a i = ( c i + c j ) / 2 a_i=(c_i+c_j)/2 ai=(ci+cj)/2
- 如果 c i + c j c_i+c_j ci+cj为奇数,如果 m ! = 2 m != 2 m!=2则赋值 a i = ( c i + c j + m ) / 2 a_i=(c_i+c_j+m)/2 ai=(ci+cj+m)/2。否则NO
const int N=1e5+10,mod=1e9+7;
int c[N];
int a[N],b[N];
int n,m;
void solve()
{
cin>>n>>m;
rep(i,0,n-1)cin>>c[i];
rep(i,0,n-1)
{
int t=n-i-1;
int x=(c[i]+c[t])%m;
if(x%2==0)x/=2;
else
{
if(m==2)
{
NO;
return;
}
x=(x+m)/2;
}
a[i]=x,a[t]=x;
b[i]=((c[i]-a[i])%m+m)%m;
b[t]=((c[t]-a[t])%m+m)%m;
}
YES;
for(int i=0;i<n;i++)cout<<a[i]<<' ';
cout<<endl;
for(int i=0;i<n;i++)cout<<b[i]<<' ';
}
C. 清楚姐姐学01背包(Easy Version)
思路
tag: 01背包,简单题
问每个物品价值增加多少可以保证出现在01背包中。
所以我们先算出不要物品i时,的最大价值,然后用maxv+1-当前价值就是最后结果
const int N=110;
int w[N],v[N];
int n,m;
int f[N];
int a[N];
void solve()
{
cin>>n>>m;
rep(i,1,n)cin>>v[i]>>w[i];
rep(i,1,n)
dwn(j,m,v[i])
f[j]=max(f[j],f[j-v[i]]+w[i]);
int maxv=f[m];
rep(k,1,n)
{
rep(i,1,m)f[i]=0;
rep(i,1,n)
{
if(i==k)continue;
dwn(j,m,v[i])
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
if(maxv>f[m])a[k]=0;
else a[k]=maxv+1-f[m-v[k]]-w[k];
}
rep(i,1,n)cout<<a[i]<<endl;
}
D. 清楚姐姐学01背包(Hard Version)
思路
tag 01背包前后缀优化
没有办法进行O(n^3),所以我们想办法将其进行优化。
f1[i][j]存背包内存放前i个物品,背包容量是j的最优解
f2[i][j]存背包内存放后i个物品,背包容量是j的最优解
思路是:必不选的最大价值-必选的价值+1
const int N=5010;
int w[N],v[N];
int f1[N][N],f2[N][N];
int a[N];
int n,m;
void solve()
{
cin>>n>>m;
rep(i,1,n)cin>>v[i]>>w[i];
rep(i,1,n)
{
rep(j,0,v[i]-1)f1[i][j]=f1[i-1][j];
rep(j,v[i],m)f1[i][j]=max(f1[i-1][j],f1[i-1][j-v[i]]+w[i]);
}
dwn(i,n,1)
{
rep(j,0,v[i]-1)f2[i][j]=f2[i+1][j];
rep(j,v[i],m)f2[i][j]=max(f2[i+1][j],f2[i+1][j-v[i]]+w[i]);
}
rep(i,1,n)
{
int res=0;
rep(j,0,m-v[i])//必选i
res=max(res,f1[i-1][j]+f2[i+1][m-v[i]-j]);
res+=w[i];
int sum=0;
rep(j,0,m)//必不选i
sum=max(sum,f1[i-1][j]+f2[i+1][m-j]);
a[i]=max(0ll,sum-res+1);
}
rep(i,1,n)cout<<a[i]<<endl;
cout<<endl;
}
signed main()
{
io;
int _;_=1;
//cin>>_;
while(_--)solve();
}
E. 清楚姐姐打怪升级
思路
tag: 数学(二分)
枚举攻击次数。推数学公式即可
const int N=1e5+10;
int n,t,a;
int h[N],v[N];
void solve()
{
cin>>n>>t>>a;
rep(i,1,n)
cin>>h[i]>>v[i];
int res=0;
rep(i,1,n)
{
if(h[i]<=a)
res++;
else
{
if(a<=v[i]*t)
{
cout<<-1<<endl;
return;
}
int pre=h[i];
h[i]-=a;
res++;
res+=(h[i]+a-t*v[i]-1)/(a-t*v[i]);
}
}
cout<<1+(res-1)*t<<endl;
}
F. 清楚姐姐学树状数组
思路
tag: 树状数组,树的遍历
/*
悲观看待成功,乐观看待失败。
author:leimingze
*/
#includeG. 清楚姐姐逛街(Easy Version)
思路
tag:搜索,暴力
先预处理zngg到达每个点的时间,然后qcjj按照地标走
const int N=1010;
int n,m;
int startx,starty;
int q;
char g[N][N];
int dist[N][N];
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
PII get(char c,int x,int y)
{
if(c=='L')
if(g[x][y-1]!='#')return {x,y-1};
if(c=='R')
if(g[x][y+1]!='#')return {x,y+1};
if(c=='U')
if(g[x-1][y]!='#')return {x-1,y};
if(c=='D')
if(g[x+1][y]!='#')return {x+1,y};
return {x,y};
}
void bfs()
{
queue<PII>q;
q.push({startx,starty});
dist[startx][starty]=0;
while(q.size())
{
auto t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int a=dx[i]+t.x,b=dy[i]+t.y;
if(a<0||a>=n||b<0||b>=m)continue;
if(g[a][b]=='#')continue;
if(dist[a][b]!=0x3f3f3f3f)continue;
dist[a][b]=dist[t.x][t.y]+1;
q.push({a,b});
}
}
}
int find(int x,int y)
{
int cnt=1;
int res=ll_INF;
while(cnt<=n*m)
{
auto t=get(g[x][y],x,y);
int a=t.x,b=t.y;
if(a==x&&b==y)
{
if(dist[a][b]==0x3f3f3f3f)
return -1;
}
if(dist[a][b]<=cnt)res=min(res,max(dist[a][b],cnt));
cnt++;
x=a,y=b;
}
return res;
}
void solve()
{
cin>>n>>m>>startx>>starty>>q;
rep(i,0,n-1)
rep(j,0,m-1)
cin>>g[i][j],dist[i][j]=0x3f3f3f3f;
bfs();
while(q--)
{
int x,y;
cin>>x>>y;
cout<<find(x,y)<<endl;
}
}
L. 清楚姐姐的三角形I
思路
tag:签到
int va,vb,vc;
void solve()
{
cin>>va>>vb>>vc;
int a=vb+vc-va;
int b=va+vc-vb;
int c=va+vb-vc;
if(a%2||b%2||c%2)NO;
else if(a+b>c&&a+c>b&&b+c>a&&abs(a-b)<c&&abs(a-c)<b&&abs(b-c)<a)
{
YES;
cout<<a/2<<' '<<b/2<<' '<<c/2<<endl;
}
else NO;
}
M. 清楚姐姐的三角形II
思路
tag:诈骗,签到
const int N=1e5+10;
int a[N];
int n;
void solve()
{
cin>>n;
a[1]=a[2]=1;
a[3]=2;
for(int i=4;i<=n;i+=3)
{
a[i]=a[i-3];
a[i+1]=a[i-2];
a[i+2]=a[i-1];
}
rep(i,1,n)cout<<a[i]<<' ';
cout<<endl;
}