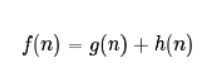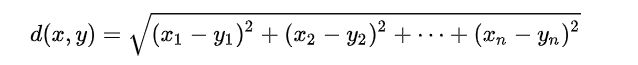[基于Python的数据结构与算法] 图

[基于Python的数据结构与算法] 图

1.图

1.1 图的定义

基本概念
顶点/边/权重	基本组成部分
度	deg(v);入度indeg(v)、出度outdeg(v)是输入边、输出边的数目
路径	边连接的顶点序列
环	起点终点相同的路径
路径长度	无权重：路径边数之和 有权重：路径上边的权重之和
邻接矩阵	以二维矩阵的形式储存权重
邻接表	以字典的形式储存权重

图的分类
边单向/双向	有向图（所有边都是单向的）/无向图
是否有环	有环图/无环图
邻接矩阵空位多/边稀少	稀疏图
任意两点都是连通的图	连通图

其他概念
生成树	具有无向连通图G 的全部顶点，但边数最少的连通子图（即任意两顶点之间有且仅有一条通路）
最小生成树	权值最小的生成树

1.2 图的实现

Vertex类：使用字典connectedTo记录每个顶点的邻接表

Graph类：使用字典vertList记录顶点（键是顶点id，值是顶点对象）

对图类中的两个顶点进行连边操作（addEdge），即对顶点对象（addNeighbor）

class Vertex:
	def __init__(self, key):
		self.__id = key
        self.__connectedTo = {}
        
    def addNeighbor(self, nbr, weight = 0):
    	self.connectedTo[nbr] = weight
    	
    def getConnections(self):
    	return self.connectedTo.keys()
    	
    def getId(self):
    	return self.id
    
    def getWeight(self, nbr):
    	return self.connectedTo[nbr]
    
    def __str__(self):
    	return str(self.id) + 'connectedTo:' + str([x.id for x in  self.connectedTo])
    	
class Graph:
	def __init__(self):
		self.__vertList = {}
		self.__numVertices = 0
		
    def addVertex(self, key):
		self.numVertices += 1
		newVertex = Vertex(key)
		self.vertList[key] = newVertex
		return newVertex
		
	def addEdge(self, f, t, cost = 0):
		if f not in self.vertList:
			newVertex = Vertex(f)
		if t not in self.vertList:
			newVertex = Vertex(t)
		self.vertList[f].addNeighbor(self.vertList[t], cost)
	
	def getVertex(self, n):
		if n in self.vertList:
			return self.vertList[n]
		else:
			return None
	
	def getVertices(self):
    	return self.vertList.keys()
    	
    def __contains__(self, n):
    	return n in self.vertList
    	
    def __iter__(self)；
    	return iter(self.vertList.values())

1.3 宽度优先搜索 BFS

BFS特性

• BFS访问完所有与起点s相距为k的顶点之后再去访问与其相距为k+1的顶点（广搜）

• BFS由队列辅助实现

• BFS以每次生成一层的方式构建一棵树，它会在访问任意一个孙节点之前将起点的所有子节点都添加进来

• 为了记录进度，BFS会将顶点标记成白色、灰色或黑色。

  颜色	意义
  白色	在构建时，所有顶点都被初始化成白色，代表该顶点没有被访问过。
  灰色	当顶点第一 次被访问时，它就会被标记为灰色。
  黑色	当BFS完成对该顶点的访问之后， 它就会被标记为黑色。

BFS实现

1. 给定图G和起点 s，BFS从起点s开始
   1. 当前顶点标记为灰色，放入Queue（此队列储存所有灰色顶点，表示待访问）中
   2. 遍历邻接表，将所有白色相邻顶点标记为灰色，依次放入Queue
   3. 当前顶点标记为黑色，访问完毕
   4. 继续访问位于Queue头部的下一个顶点，重复该四步直到Queue为空

• Vertex类新增属性distance、predecessor、color用来表示顶点的路径长度、上一顶点、颜色状态

  class Vertex:
  	def __init__(self, key):
  		self.__id = key
          self.__connectedTo = {}
          self.__distance = 0
          self.__predecessor = None
          self.__color = 'white'
          
      def setDistance(self, dis):
      	self.__distance = dis
      	
      def setPred(self, ver):
      	 self.__predecessor = ver
      	 
      def setColor(self, color):
      	self.__color = color
      
      def getDistance(self):
      	return self.__distance
      	
      def getPred(self):
      	return self.__predecessor
      	
      def getColor(self):
      	return self.__color
  

• 以上类可通过调用第三方库实现，得到BFS算法

  from pythonds.graphs import Graph, Vertex
  from pythonds.graphs import Queue
  
  #BFS算法实现
  def BFS(self, start):
  	start.setDistance(0) 
  	start.setPred(None)
  	vertQueue = Queue( )
  	vertQueue.enqueue(start)
  	while vertQueue.size() > 0:
  		currentVert = vertQueue.dequeue ( )
  		for nbr in currentVert.getConnections():
  			if nbr.getColor() == 'white':
  				nbr.setColor('gray')
  				nbr.setDistance(currentVert.getDistance() + 1)
  				nbr.setPred(currentVert)
  				vertQueue.enqueue(nbr)
  		currentVert.setColor('black')
  

BFS性能分析

BFS
空间复杂度	O(V)
时间复杂度	O(V+E)

1.4 深度优先搜索 DFS

DFS特性

• DFS尽可能深地搜索树的分支（深搜）

• DFS通过递归回溯隐式地使用栈

• 一次深度优先搜索甚至能够创建多棵深度优先搜索树，称为深度优先森林

• 为了记录进度，DFS会将顶点标记成白色、灰色或黑色，同BFS

DFS实现（通用DFS）

DFS步骤图示

1. 给定图G和起点 s，DFS从起点s开始

   1. 当前顶点标记为灰色，遍历其邻接表中的相邻顶点
   2. 检查相邻顶点的颜色状态，对白色顶点进行递归调用，重复以上操作

2. 直到最后的顶点无相邻白色顶点，层层回溯

from pythonds.graphs import Graph

class DFSGraph(Graph):
	def __init__(self):
		super().__init__ ()#继承父类构造函数中的内容，且子类可在父类的基础上补充
		self.time = 0#记录最短路径长度
	
	def DFS(self):
		#遍历图中所有顶点，确保深度优先森林中的所有顶点都在考虑范围内，而不会有被遗漏的顶点
		for aVertex in self:
			aVertex. setColor('white')
			aVertex. setPred(-1)
		for aVertex in self:
			if aVertex.getColor() == 'white':
				self.DFSvisit(aVertex)

	def DFSvisit(self, startVertex):
    	startVertex.setColor('gray')
		self.time += 1
		startVertex.setDiscovery(self.time)
		for nextVertex in startVertex.getConnections():
			if nextVertex.getColor( ) == "white': 
				nextVertex.setPred(startVertex)
				self.DFSvisit(nextVertex)
		startVertex.setColor('black')
		self.time += 1
		startVertex.setFinish(self.time)

DFS性能分析

DFS
时间复杂度	O(V + E)

骑士周游问题（Warnsdorff算法）

[ 问题描述 ]

取一块国际象棋8×8的棋盘和一颗骑士棋子（马），在骑士的走法规范下，找到一系列合适的路径，使得骑士对棋盘上的每一格刚好都只

访问一次。

[ 算法实现 ]

from pythonds.graphs import Graph, Vertex

def knightTour(n, path, u, limit):
	'''
	n 是搜索树的当前深度；
	path 是到当前为止访问过的顶点列表；
	u 是正在访问的顶点；
	limit 是顶点总数。
	'''
	
	#顶点正在被访问：标记为灰色，加入路径列表
	u.setColor('gray')	
	path.append(u)
	
	if n < limit:
		#获取该顶点相邻顶点列表
		nbrlist = list(u.getConnections())
		i= 0
		done = False
		
		#1.相邻顶点列表第一项符合条件，进行下一顶点递归调用
		#2.回溯时返回此步，依次索引相邻列表顶点
		while i < len(nbrlist) and not done:
			if nbrList[i].getColor() == 'white' :
				done = knightTour(n+1, path, nbrList[i], limit)
			i += 1
		
		'''
		若该顶点是死路（无出边指向顶点len(nbrlist) = 0/相邻顶点无白色nbrList[i].getColor() ！= 'white'）
		准备回溯（重新标记为灰色，移出路径列表）
		结束该次调用，回到上一层调用
		'''
		if not done: 
			path.pop( )
			u.setColor('white')
	
	else:
		'''
		搜索树的当前深度（n） = 顶点总数（limit），
		完成一次周游。
		'''
		done = True 
		
	return done

算法改进：

为了保证接下来要访问的顶点有最少的合理走法，每次选择下一个要访问的顶点至关重要。如果选择优先访问合理走法最少的顶点，则骑士优可以先访问棋盘边缘的格子。这样做保证了骑士能够尽早访问难以到达的角落，并且在需要的时候通过 中间的格子跨越到棋盘的另一边。而不是在周游的前期就访问位于棋盘中间的格子，因而被困在棋盘的一边，而无法到达另一边的那些没访问过的格子。

利用这类知识来加速算法被称为启发式搜索算法（heuristic)，本例中启发式算法被称为Warnsdorff算法。

而DFS与BFS被称为盲目式搜索算法。

def Warnsdorff(n):
	resList = [ ]
	for v in n.getConnections():
		if v.getColor() == 'white' :
			C = 0
			for W in v.getConnections() :
				if w.getColor() == 'white' :
					C += 1
			resList. append((c, v))
	resList.sort(key = lambda x: x[0]) 
	orderByAvail = [y[1] for y in resList]
	return orderByAvail

1.5 最短路径问题/寻路算法

1.5.1 Dijkstra算法

采用贪心模式。类似于BFS，用于解决有权重的图。时间复杂度为O(（V + E）logV)

from pythonds.graphs import PriorityQueue, Graph, Vertex

# Vertex类中的distance属性初始值默认设置无穷大（实际一般将其设为一个大于所有可能出现的实际距离的值）

def Dijkstra(aGraph, start):
	pq = PriorityQueue()
	start.setDistance(0)
	
	pq.buildHeap([(v, v.getDistance()) for v in aGraph])
	
	while not pq.isEmpty():
		currentVert = pq.delMin()
		for nextVert in currentVert.getConnections() :
			newDist = currentVert.getDistance() + currentVert.getweight(nextVert)
			if newDist < nextVert.getDistance():
				nextVert.setDistance(newDist)
				nextVert.setPred(currentVert)
				pq.decreaseKey(nextVert, newDist) #此方法将新产生/更新后的（路径， 节点）键值对添加到优先队列中

以此图为例分析 Dijkstra算法 实现过程

1. pq = [(0, u), (SysMaxInit, v), (SysMaxInit, w), (SysMaxInit, x)] 进入循环前
2. pq = [(1, x), (2, v), (5, w)] 结束第一次循环
3. pq = [(2, v), (2, y), (4, w)] 结束第二次循环
4. pq = [(2, y), (4, w)] 结束第三次循环
5. pq = [(4, w), (3, z)] 结束第四次循环
6. pq = [(3, z)] 结束第五次循环
7. pq = [] 跳出循环

1.5.2 贪婪最佳优先搜索算法(Greedy Best-First Search，GBFS)

from pythonds.graphs import PriorityQueue, Graph, Vertex

def GBFS(start, goal):
    frontier = PriorityQueue()
    frontier. insert((start, 0))
    came_from = dict()	#记录上一顶点，跟踪路径
    cost_so_far = dict()
    came_from[start] = None			
    cost_so_far[start] = 0

    while not frontier. isEmpty():
       current = frontier. delMin()

       if current == goal:
          break

       for next in current. getConnections():
          if next not in cost_so_far: #相当于a*的h(n),每个顶点是一定的，无需比较更新
             cost_so_far[next] = new_cost
             priority = new_cost + heuristic(goal, next) #启发函数，具体意义见a*
             frontier.put((next, priority))
             came_from[next] = current

1.5.3 A*算法

一种启发式算法，每个顶点的优先级基于如下函数：

• f(n)/cost 是 顶点n的综合代价。下一个要遍历的顶点就是综合优先级最高（代价值最小）的顶点。
• g(n) /g-cost 是 顶点n距离起点的实际代价。
  • 如果 g(n)为0，即只计算任意顶点 n 到目标的估计代价 h(n)，而不计算顶点 n 距离起点的实际代价，则算法转化为使用贪心策略最佳搜索算法（GBFS），速度最快，但可能得不出最优解
• h(n)/h-cost 是 顶点 n 到目标的估计代价，也就是A*算法的启发函数。
  • 如果h(n)为0，即只计算顶点 n 距离起点的实际代价g(n)，而不计算顶点 n 到目标的估计代价，则算法转化为Dijkstra算法，此时需要计算最多的顶点
  • 如果h(n)不大于顶点 n 到目标的实际距离，则一定可以求出最优解，而且 h(n)越小，需要计算的节点越多，算法效率越低

常用的启发函数有：

• 曼哈顿距离（Manhattan distance）—— 如果图形中只允许朝上下左右四个方向移动

  • 欧几里得空间的直角坐标系上两点间横纵坐标间线段长度的和：

    

  • 代码实现

    def heuristic(node):
        dx = abs(node.x - goal.x)
        dy = abs(node.y - goal.y)
        return D * (dx + dy)
    
    #这里D是指两个相邻节点之间的移动代价，通常是一个固定的常数
    

• 欧几里得距离（Euclidean distance）—— 如果图形中允许朝任何方向移动

  • 欧几里得空间中两点的直线距离：

  • 代码实现

    def heuristic(node) =
        dx = abs(node.x - goal.x)
        dy = abs(node.y - goal.y)
        return D * sqrt(dx * dx + dy * dy)
        
    #这里D是指两个相邻节点之间的移动代价，通常是一个固定的常数
    

A*算法代码实现

from pythonds.graphs import PriorityQueue

def a_star(graph, start, goal):
    frontier = PriorityQueue()
    frontier. insert((start, 0))
    came_from = dict()	#记录上一顶点，跟踪路径，最短路径再不断更新
    cost_so_far = dict()  #记录每一次遍历时顶点g(n)的状态，以便更新
    came_from[start] = None			
    cost_so_far[start] = 0

    while not frontier. isEmpty():
       current = frontier. delMin()

       if current == goal:
          break

       for next in current. getConnections():
          new_cost = cost_so_far[current] + current. getWeight(next)
          if next not in cost_so_far or new_cost < cost_so_far[next]:  
             #每个顶点的h(n)是一定的，因此每次只需重新计算比较g(n)
             cost_so_far[next] = new_cost
             #而优先队列中的优先级由h(n)和g(n)共同决定，PriorityQueue记录顶点f(n)的状态
             priority = new_cost + heuristic(goal, next)
             frontier.put((next, priority))
             came_from[next] = current

参考资料

• 维基百科

• python数据结构与算法分析第2版

• 算法可视化讲解网站-RedBlogGames

• 知乎-路径规划之A算法 及其算法实现 Github-aAlgorithm

重新计算比较g(n)
cost_so_far[next] = new_cost
#而优先队列中的优先级由h(n)和g(n)共同决定，PriorityQueue记录顶点f(n)的状态
priority = new_cost + heuristic(goal, next)
frontier.put((next, priority))
came_from[next] = current

### 参考资料

- 维基百科

- python数据结构与算法分析第2版

- [算法可视化讲解网站-RedBlogGames](https://www.redblobgames.com/)

- [知乎-路径规划之A*算法](https://zhuanlan.zhihu.com/p/54510444) 及其算法实现 [Github-a*Algorithm](https://github.com/paulQuei/a-star-algorithm)