高效寻路算法——A*（A-Star）

在数据结构中我们学过图，而图中一个很重要的课题就是与最短路径、最优路径相关的寻路问题，包括Dijkstra、深度优先搜索，都是其中的经典算法；

同时，在游戏开发中，也常常需要设计合适的寻路算法来实现怪物AI的移动、人物自动寻路等常用功能，在各种算法中，A*无疑是最常用也是最经典的一种，作为进一步了解游戏寻路机制的基础，A*的学习很有必要，因此接下来这篇文章会从原理入手，一步步解析算法的过程并且实现它

图0
经典RPG中人物NPC的移动往往就需要合适的寻路算法，地图的网格化就是为了实现这点

---

一、算法介绍

       A*算法是静态网络中求解最短路径时最有效的直接搜索算法，也是许多算法的启发式算法。因其简单高效的特点，常常会用作游戏中的寻路算法。当然要注意，在直接搜索算法中它是最有效的，后来也出现了许多预处理算法（如ALT，CH，HL等等），在线查询效率是A*算法的数千甚至上万倍。

 

二、算法原理

        A*算法的本质似乎是一种贪心选择策略，即走的每一步都是当前状况下的最优选择，而A*算法的贪心选择依据主要是三个值F、H和G和两个表openList和closeList；首先先来解释一下它们各自的含义：

        G——从起点到达当前位置点的移动代价/距离，这个值是会不断累加并更新的；我们将横向或纵向（即上下左右）移动一格的代价定为10，那么斜向移动一格的代价可以定为14（即），使用10作为单位代价是为了避免小数计算。不同的路径会使得起点到达当前位置的移动代价并不相同，但是我们总是倾向于更小的G值，这是由贪心选择策略导致的，后面会看到这一点。

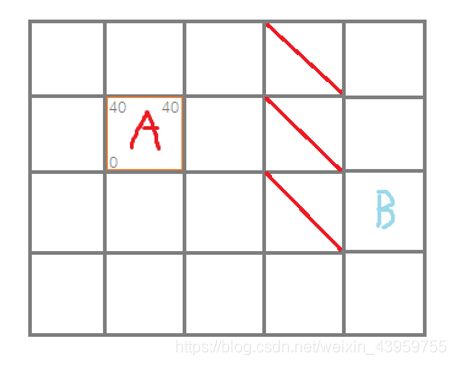
        H——从当前位置到达终点的估计代价/距离，计算估计代价的方法有很多，我们这里仅讨论一种较为简单且常用的方法即曼哈顿(Manhattan)距离，曼哈顿距离表示两个点的绝对轴距总和，如图1所示。

图1

       F——当前位置的总代价，也是进行贪心选择的最终依据，其值为移动代价与估计代价的值的和，即F = G + H。

       openList——开放列表，用于保存当前可以到达的所有位置节点；我们每次都要从openList中寻找F值最小的节点作为当前节点，然后再将当前节点周围所有可到达的点加入到openList当中并将当前节点设置为它们的父节点，如果已经在openList当中，则需要判断从这个点到当前节点的代价是否更小，有必要则进行更新。这样，当把终点加入到openList中时，就可以回溯父节点找到一条最短路径；如果到openList为空时，终点仍未添加进去，则说明查找失败，无法到达终点。

       closeList——关闭列表，用于保存开放列表中处理完的节点，保证处理过的节点不再处理，通常可以和图中不可到达的位置记录在同一个表中。

 

三、算法过程

1、将起点加入到openList中（每次将点加入到openList当中时，都要计算并保存它们的F值，后面不再赘述），将所有不可到达的点记录在closeList当中

2、重复进行下面步骤，直到openList为空或者将终点添加至openList中：

（1）从openList中取出F值最小的节点，将该点作为当前要处理的节点；

（2）遍历该当前点周围的可到达点（即八个方向且不在closeList中的点），如果这个可到达点不在openList中，直接将其加入进来，并将它的父节点设置为当前点；如果这个可到达点已经在openList当中，那么需要比较经由这个点到达当前处理点的路径代价是否会更小（因为H值不变，所以主要目标是比较G值大小），如果代价更小，那么就改变当前处理点的父节点为这个点，否则不作任何处理，这样是为了保证到达当前处理点的路径是最短的；

图2
例如图2所示，考察当前处理点周围的可加入点时，因为其上方的格子已经在openList当中，所以需要比较经由其上方格子到达当前格子的代价是否更小，很明显
Ga = 10 + 10 = 20;
Gb = 14;
Gb < Ga;
因此比较而言路线b的代价更小，当前待处理格子不需要作任何改变

（3）将该处理点记录到closeList当中

3、从终点开始，开始沿着父节点遍历至起点，就是利用A*算法所得到的最短路径

 

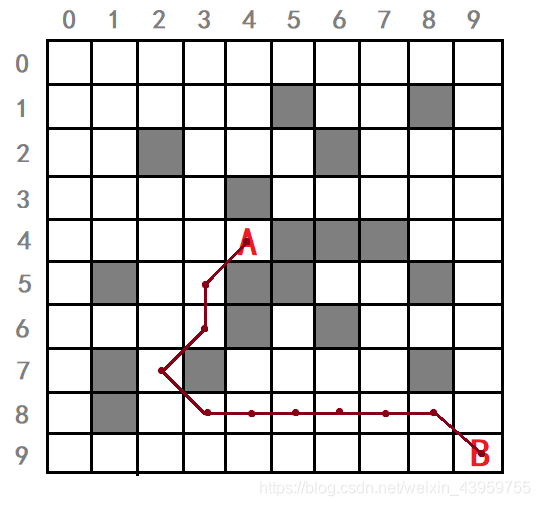
如图3456，以一个实例的形式展现了寻找从起点A到终点B的最短路径的过程

图3
一开始openList当中只有A一个节点，因此取出F值最小的节点也就是A作为当前的待处理节点

图4
处理节点A，将其周围所有的可到达节点加入到openList中，因为这些可到达节点一开始都不在openList当中，因此不需要比较G值直接加入并将A设置为他们的父节点，然后取出openList中F值最小等于34的节点即右下角的节点作为下一个待处理节点；这样节点A处理完毕，将A加入到closeList当中

图5
处理当前F值等于34的节点，先考察其周围的节点，节点A因为已经处理完毕置于closeList当中，其右上角和右边的节点是不可到达节点，因此这些点无需考虑；其下方三个节点并不在openList当中，因此直接将他们加入openList，最后考察剩下两个点，比较可得经过他们的G值均大于原来的G值，因此它们并非是更优路径，不作任何改变；如此一来当前F值等于34的这个节点也处理完毕，我们将其加入到closeList当中

图6
反复重复上面的步骤，最终将B节点加入到openList当中，表示搜索成功，然后我们从终点B开始，访问它们的父节点，就可以得到一条从A到B的最短路径啦！即图中棕色箭头表示的路径

 

四、代码实现

#define MAX 10
#include
#include
#include
#include
#include"priorQue.h"

using namespace std;

typedef struct vector2 {
	int x, y;
}vector2;
//定义一个二维向量结构体

typedef struct AStarNode {
	vector2 pos, parent;
	int F, G, H;  //节点的位置和代价

	AStarNode() {}
	AStarNode(int x1, int y1, int x2, int y2) {
		parent = { -1, -1 };  pos = { x1, y1 };
		H = abs(x1 - y1) + abs(x2 - y2);
		G = 0;  F = H;
	}
	//构造函数，用于初始化位置坐标和计算估计代价

	bool operator<(const AStarNode &n)const {
		return this->F < n.F;
	}
	//重载运算符小于号，这样才能用最小堆进行存储
}AStarNode;
//A*节点

bool AStar(int visit[][MAX], int x1, int y1, int x2, int y2) //传入的参数分别是地图信息、起点的xy坐标、终点的xy坐标
{
	/*
	visit数组用于记录图中点的当前状态
	如果等于0，代表这个点不可到达或者已经被置入closeList当中，因此visit数组实现了closeList表的功能
	如果等于1，为正常状态，说明这个点能走通
	如果等于2，说明见当前这个点位于openList当中
	*/

	AStarNode a[MAX][MAX];
	//开一个与图等大的节点数组
	vector2 around[8] = { {-1, 1}, {0, 1}, {1, 1}, {-1, 0}, {1, 0}, {-1, -1}, {0, -1}, {1, -1} }, tmp = { 0, 0 };
	//around数组表示一个点周围的八个方向
	AStarNode start(x1, y1, x2, y2), current;
	a[x1][y1] = start;
	//初始化起点和当前待处理的节点
	bool flag = false;
	//记录终点是否被加入到openList当中
	stack record;

	priorQue openList;
	openList.enQueue(start);
	//将openList用优先级队列来表示，这样队列首部第一个节点自然就是F值最小的节点
	//先将起点加入到openList中去

	while (!openList.empty() && !flag) 
	{
		current = openList.deQueue();  //从openList中选出F值最小的作为当前待处理的节点
		for (int i = 0; i < 8; i++) 
		{
			tmp.x = current.pos.x + around[i].x;
			tmp.y = current.pos.y + around[i].y;
			if (tmp.x < 0 || tmp.x > MAX - 1 || tmp.y < 0 || tmp.y > MAX - 1 || visit[tmp.x][tmp.y] == 0) continue;
			//得到当前待处理点周围的一个点，若这个点超出边界或者为不可到达点，则跳过不作处理
                        if (around[i].x != 0 && around[i].y != 0 && 
                            visit[current.pos.x + around[i].x][current.pos.y] == 0 && visit[current.pos.x][current.pos.y + around[i].y] == 0) continue;
                        //另外一种情况，即侧向虽然可达，但无法直接到达，也应跳过

			if (visit[tmp.x][tmp.y] == 1) {
				//如果visit等于1
				AStarNode n(tmp.x, tmp.y, x2, y2);
				n.parent = current.pos;
				if (abs(around[i].x) + abs(around[i].y) > 1) n.G = current.G + 14;
				else n.G = current.G + 10;
				n.F = n.G + n.H;
				//计算这个点的G值和F值
				openList.enQueue(n);
				a[tmp.x][tmp.y] = n;
				visit[tmp.x][tmp.y] = 2;
				//直接加入openList当中
				if (tmp.x == x2 && tmp.y == y2) {
					flag = true;
					current = n;
				}
				//如果这个加入点为终点，将标记记为true
			}
			else {
				//如果visit等于2
				AStarNode n = a[tmp.x][tmp.y];
				int price = 10;
				if (abs(around[i].x) + abs(around[i].y) > 1) price = 14;
				if (n.G + price < current.G) {
					current.G = n.G + price;
					current.parent = n.pos;
				}
				//需要判断从这个点到达待处理点是否为更优路径,如果是则进行改动
			}
		}
	}
	if (flag) {
		while (current.pos.x != x1 || current.pos.y != y1) {
			record.push(current);
			current = a[current.parent.x][current.parent.y];
		}
		record.push(current);
		while (!record.empty()) {
			cout << "(" << record.top().pos.x << " ," << record.top().pos.y << ") " << record.top().F << endl;
			record.pop();
		}
	}
	//终点加入openList中，说明搜索成功，从终点开始访问父节点至起点并用栈来储存；之后再遍历一遍栈将路径打印出来

	return flag;
}
//A*算法主体

int main()
{
	int map[MAX][MAX] = {
		1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
		1, 1, 1, 1, 1, 0, 1, 1, 0, 1,
		1, 1, 0, 1, 1, 1, 0, 1, 1, 1,
		1, 1, 1, 1, 0, 1, 1, 1, 1, 1,
		1, 1, 1, 1, 1, 0, 0, 0, 1, 1,
		1, 0, 1, 1, 0, 0, 1, 1, 0, 1,
		1, 1, 1, 1, 0, 1, 0, 1, 1, 1,
		1, 0, 1, 0, 1, 1, 1, 0, 1, 1,
		1, 0, 1, 1, 1, 1, 1, 1, 1, 1,
		1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
	};
	cout << AStar(map, 4, 4, 9, 9) << endl;

	system("pause");
}
//编造数据进行测试

 

五、结果演示

将最短路径的节点坐标和F值依次打印出来（测试数据较少，有错误欢迎随时指正）。

结果如图7所示：

图7

图8 根据程序运行结果画出的最优路径

 

参考文章

https://blog.csdn.net/hitwhylz/article/details/23089415