(算法理论)动态规划（python）

动态规划

基本思想

若要解一个给定问题，我们需要解其不同部分（即子问题），再合并子问题的解以得出原问题的解。 通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量： 一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用

明确三个事情：

1. 目标问题
2. 状态的定义：opt[n]
3. 状态转移方程：opt[n]=best_of(opt[n-1]，opt[n-2])

分治与动态规划

共同点：二者都要求原问题具有最优子结构性质,都是将原问题分而治之,分解成若干个规模较小(小到很容易解决的程序)的子问题.然后将子问题的解合并,形成原问题的解.

不同点：分治法将分解后的子问题看成相互独立的，通过用递归来做。
动态规划将分解后的子问题理解为相互间有联系,有重叠部分，需要记忆，通常用迭代来做。

步骤

1. 求一个问题的最优解
2. 大问题可以分解为子问题，子问题还有重叠的更小的子问题
3. 整体问题最优解取决于子问题的最优解（状态转移方程）
4. 从上往下分析问题，从下往上解决问题
5. 讨论底层的边界问题

动态规划最重要的有三个概念：1、最优子结构 2、边界 3、状态转移方程

引出：

由一个简单的问题来解释为什么要使用动态规划:
有十个台阶，从上往下走，一次只能走一个或两个台阶，请问总共有多少种走法？

1. 最优子结构：我们来考虑要走到第十个台阶的最后一步，最后一步必须走到第八或者第九。不难得到 f(10) = f(9)+f(8)、f(9) = f(8)+f(7)·····
2. 边界：f(1) = 1, f(2) = 2
3. 状态转移：f(n) = f(n-1) + f(n-2)

简单粗暴的递归解法：

def get_count(n):
    if n == 1:return 1
    if n == 2:return 2
    else:
        return get_count(n-1)+get_count(n-2)
print(get_count(10))

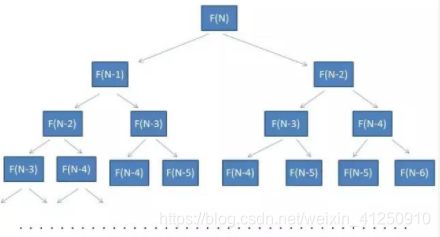
很显然这是一个满二叉树，高度为N-1。所以总节点数为$2^{N-1}$,时间复杂度为O($2^N$) 。看着就恐怖。递归计算方法，我们不难看出，$2^{N-1}$个节点产生了大量重复的运算。找到问题的根源，对应的解决方法就应运而生，那就是从下往上算，把以前计算过的数值，保存在一个哈希表中，然后后面计算时先查询一下，存在就无需计算。时间复杂度为O(n) ,空间复杂度为O(n)。但是在仔细一想其实，无需保存所有的$f$,每个$f$都只与前两个值相关，所以空间复杂度可以降低为O(1).我们来看看相关代码。

自底向上求解

动态规划算法的核心是记住已经求过的解，先计算子问题，再由子问题计算父问题。

def get_count(n):
    if n == 1:return 1
    elif n == 2 :return 2
    else:
        l = [1,2]
        for i in range(3,n):
            l[0],l[1] = l[1],l[0]+l[1]
        return l[0]+l[1]

下面给出一些使用常见的动态规划相关的面试题，通过python实现：

问题一：连续子数组最大和

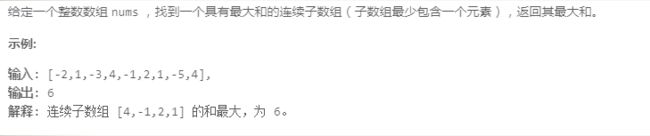
定义$M[j]$：以$j$结尾的字串中，和最大值
状态转移：$M[j]$=max {$M[j-1]+A[j]，A[j]$}

def max_subarry(nums):
    m = nums[0]
    tem_m = nums[0]
    for i in range(1,len(nums)):
        if tem_m<=0:
            tem_m = nums[i]
        else:
            tem_m+=nums[i]
        if tem_m > m:
            m = tem_m
    return m

问题二：数字和为sum的方法数

dp问题，节省空间用一维数组解：
dp长度为m+1的数组，表示和为下标所具备的方案

n, m = [int(i) for i in input().split()]
a = [int(x) for x in input().split()]
dp = [0 for i in range(m+1)]
dp[0] = 1
for i in range(n):
    j = m
    while j>=a[i]:
        dp[j] += dp[j-a[i]]
        j -= 1
print(dp[m])

问题三：最长上升子数列

定义$L[j]$: 到位置$j$为止，找到的最长上升字串长
状态转移：$L[j]=ma{x}_{i<jandA[i]<A[j]}$ { $L[i]$}+1

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums)<=1:
            return len(nums)
        opt=[1]*len(nums)
        for i in range(1,len(nums)):
            for j in range(i):
                if nums[i]>nums[j]:
                    opt[i]=max(opt[i],opt[j]+1)
        return max(opt)

问题四：零钱兑换

定义：$M[j]$：总金额为$j$时，所需要最少的硬币个数
状态转移：$M[j]$= $mi{n}_i$ {$M[j-v_i]$ } +1

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        if len(coins)==0:
            return -1
        if amount==0:
            return 0
        if len(coins)==1 and coins[0]>amount:
            return -1
        m=[-1]*(amount+1)
        m[0]=0
        for i in range(1,amount+1):
            cur_min=amount+1
            for c in coins:
                if c<=i:
                    cur_min = m[i-c] if m[i-c]

问题五：0-1背包问题

价值数组v: {8,10,6, 3, 7, 2}
重量数组w:{4, 6, 2, 2, 5, 1}
背包容量:C=12

定义$M[i,j]$：可选择前$i$个物品时，最大容量为$j$的最大重量
转移方程 ：$M[i,j]$=max{$M[i-1,j]$,$M[i,j-v_i$]+$v_i$}

$M[i,j]$的值：

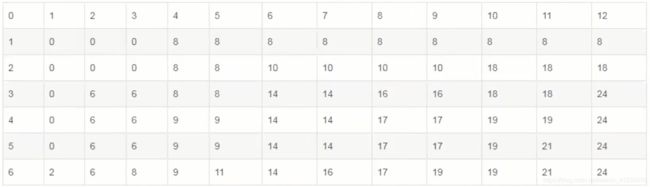
注：从左往右，一行一行的依次更新，更新每行时只需考虑 ：是否加入新物品

import numpy as np
def knapsack(w,v,C):
	mem=np.zeros((len(w)+1,C+1))
	for i in range(1,len(w)+1):
		for j in range(1,C+1):
			if w[i-1]<=j:
				mem[i,j]=max (mem[i,j],mem[i-1,j],mem[i-1,j-w[i-1]]+v[i-1])
			else:
				mem[i,j]=mem[i-1][j]
	return mem[-1][-1]