识别电动汽车车牌并使用自动充电车充电的方案

主要参考：1.用MATLAB实现基于A*算法的路径规划； 2.车牌识别系统；3. 路径规划五种算法简述

下面都是写给自己看的，没地方存储才放上来的。因为大部分都是copy上面两个的，所以放上来不太好。

一、车牌识别

用户在APP上下单时需要输入自己车辆的车牌号，这样允许充电车在给电动汽车充电前检查其是否为目标车辆。一个完整的车牌号识别系统要完成从图像采集到字符识别输出，过程相当复杂，基本可以分成硬件部分跟软件部分，硬件部分包括系统触发、图像采集，软件部分包括图像预处理、车牌定位、字符分割、字符识别四大部分，一个车牌识别系统的基本流程如图1所示，硬件部分和软件部分紧密衔接。

图1 车牌识别系统流程

本项目基于MATLAB设计出一个车牌识别程序，并将其封装为函数number_plate。该程序对电动汽车车牌号进行识别与提取，包括图像预处理，基于车牌颜色特征的定位方法，车牌倾斜校正，字符分割，字符识别五个部分。对这个识别程序进行仿真测试，得到了较为准确的识别结果。使用的原始图像之一如图2所示。

图2 原始图像之一

1. 图像预处理

一般预处理的具体操作包括规整大小、噪声滤波、腐蚀、平滑、规整为统一大小便于后续处理的参数设置等。由于图片的分辨率较低，所以此处大范围的腐蚀和平滑图片的操作不仅没有有效地去除噪声，还使图像变得模糊不清，降低了识别率。所以项目在图像预处理部分仅对图像进行中值滤波操作，后续利用形态学处理进一步去噪。针对彩图的中值滤波需要将图片的R、G、B三个色道分别提取出来，分别滤波。这里采用3x3的中值滤波算子，对三个色道分别滤波，然后使用cat函数将三色道整合起来。

对图2进行中值滤波处理后的结果如图3所示。

图3 中值滤波结果

2. 车牌定位

程序中使用的是一种基于颜色特征的定位算法，该算法不用对整幅图像进行边缘检测，而是直接寻找图片中颜色、形状及纹理符合车牌特征的连通区域。通过对大量车牌图像的分析，可以发现对于具有某种目标色的像素，可以直接通过对H、S、V三分量设定一个范围来把它们过滤出来，无需进行较复杂的色彩距离计算，这样可以在色彩分割时节省大量的时间。这种过滤对绿色、蓝色、黄色等车牌特别有效，但对于黑色和白色的过滤效果不是很理想。这是因为对于纯色的黑色和白色，它们的色调和饱和度没有意义，所以和其它颜色相比缺少了两个过滤指标。通过查阅相关资料得到汽车车牌的HSV值，具体如表1所示。

表1  HSV取值范围

项目	绿色	蓝色	黄色	白色	黑色
色调	70-150度	200-255度	25-55度	\	\
饱和度	0.4-1	0.4-1	0.4-1	0-0.1	\
亮度	0.3-1	0.3-1	0.3-1	0.9-1	0-0.35

国内电动汽车都使用绿色渐变的车牌，根据彩色图像的RGB比例定位出近似绿色的候选区域，但是由于RGB三原色空间中两点间的欧氏距离与颜色距离不成线性比例，在设定绿色区域的定位范围时不能很好的控制，因此造成的定位出错是最主要的。这样在图片中出现较多的绿色背景情况下识别率会下降，不能有效提取车牌区域。对此采取自适应调节方案。对分割出来的区域进行识别调整。根据长宽比，绿白色比对候选区域进行多次定位，最终找到车牌区域。

3. 车牌倾斜校正

在车牌识别系统中，车牌字符能够正确分割的前提是车牌图像能够水平，以使水平投影和垂直投影能够正常进行。车牌矫正是车牌定位和字符分割的一个重要处理过程。经过车牌定位后所获取的车牌图像不可避免地存在某种程度的倾斜，这种倾斜不仅会给下一步字符分割带来困难，最终也将对车牌的识别的正确率造成直接的影响。所以应尽早检查倾斜角度，做倾斜校正。程序中运用Radon变换算法对车牌进行矫正，其原理就是将数字图像矩阵在某一指定角度射线方向上做投影变换。这就是说可以沿着任意角度θ来做Radon变换。

最后校正结果如图4所示。

图4 车牌倾斜校正结果

4. 形态学处理与边框去除

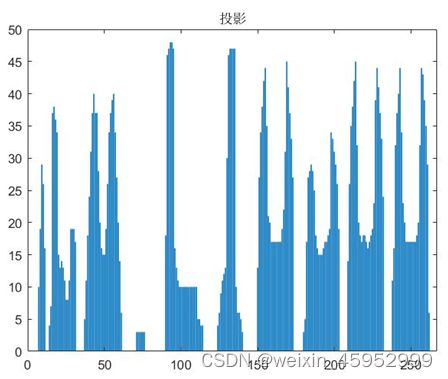
对已经获得的图像进行二值化处理，接着针对二值图像使用bwmorph函数进行形态学运算，删除里面具有H连接的像素和杂散像素并执行形态学开运算（先腐蚀后膨胀）。之后利用字符的投影去除图片中车牌的边框。其中投影图如图5所示，处理结果如图6所示。

图5 投影图

图6 处理结果

5. 字符分割

在电动汽车牌照识别过程中，将牌号分割利于后续的字符识别。字符分割一般采用垂直投影法。由于字符在垂直方向上的投影必然在字符间或字符内的间隙处取得局部最小值，并且这个位置应满足牌照的字符书写格式、字符、尺寸限制和一些其他条件，所以利用垂直投影法对复杂环境下的汽车图像中的字符分割有较好的效果。

程序字符分割的具体算法如下：

(1)确定图像中字符的大致高度范围：先自下而上对图像进行逐行扫描，直到遇到第一个黑素像素，记下行号，然后自上而下对图像进行逐行扫描，直到遇到第一个黑素像素，记下行号。这两个行号就标志出了字符大致的高度范围。

(2)确定每个字符的左起始和右终止位置：在第一步得到的高度范围内进行自左向右逐列扫描，遇到第一个黑色像素时，认为是字符分割的起始位，然后继续扫描，直到遇到有一列中没有黑色像素，认为是这个字符的右终止位置，准备开始进行下一个字符的分割。按照上述方法继续扫描，直到扫描到图像的最右端。这样就得到了每个字符的比较精确的范围。

(3)在已知的每个字符比较精确的宽度范围内，再按照第一步的方法，分别自下而上和自上而下，逐行扫描，来获取每个字符精确的高度范围。

分割车牌字符左右边界时，通过垂直扫描过程，由于数字和字母具有连通性，所以分割数字和字母比较容易。通过垂直扫描过程，统计黑色像素点的个数，由于两个字符之间没有黑像素，所以可以作为字符分割的界限。

 (4)由于图像采集时图像的像素值不一样，经切割出来的字符的大小也会不一样，所以在进行匹配前先使用imresize函数进行字符图像的缩放处理，使图像大小跟模板图像大小一致。

图7 字符分割结果

6. 字符识别

本系统采用的对车牌识别算法是模板匹配算法，模板匹配是将从待识别的图像或图像区域中提取的若干特征量与模板相应的特征量逐个进行比较，计算它们之间规格化的互相关量，其中互相关量最大的一个就表示期间相似程度最高，可将图像归于相应的类。

字符识别结果如图8所示。

图8 字符识别结果

 

识别模块封装后结果如下所示。

% %清空环境
% clc;          %清空命令行
% clear all;    %清除工作空间所有变量
% close all;    %关闭所有图形窗口
 
function [plate_num_str]=number_plate()
%=====================读入图片=========================
[fn,pn,fi] = uigetfile('汽车图片\*.jpg','选择图片');%显示检索文件的对话框 fn返回的文件名 pn返回的文件的路径名 fi返回选择的文件类型 
I = imread([pn fn]);                %读入彩色图像
figure('NumberTitle','off','Name','原始图像');
imshow(I);title('原始图像');        %显示原始图像
 
% 对彩图进行中值滤波
R=I(:,:,1);  
G=I(:,:,2);  
B=I(:,:,3);  
 
R=medfilt2(R,[3,3]);
G=medfilt2(G,[3,3]);
B=medfilt2(B,[3,3]);
 
I=cat(3,R,G,B);  % 对彩色图像R,G，B三个通道分别进行3×3模板的中值滤波 cat函数用于连接两个矩阵或数组
figure('NumberTitle','off','Name','中值滤波图像');
imshow(I);title('中值滤波图像');        %显示中值滤波图像

%==================加入进度条===========================
waitbar_;
 
%================图像分割区域(车牌定位)==========================
picture =image_segmentation(I);
threshold=50;
 
%========================倾斜校正=================
[picture_1,angle] = rando_bianhuan(picture); %倾斜校正  picture 返回校正后的图片 angle 返回倾斜角度
 
%=========================形态学操作====================
picture_6 = xingtaixue(picture_1);%主要对图像
 
%=============对图像进一步裁剪，保证边框贴近字体===========
bw = caijian(picture_6);
 
%=================文字分割 ===================================
image=qiege(bw);
 
%=================显示分割图像结果================================
bb =zifu_shibie(image);
imshow(picture_1),title (['识别车牌号码:', bb],'Color','r');
 
%=====================导出文本===========================
% fid=fopen('Data.txt','a+');
% fprintf(fid,'%s\r\n',bb,datestr(now));
% fclose(fid);
 
% %===================读出声音============================
% duchushengyin(bb);
plate_num_str=bb;
end


%% 图像分割函数image_segmentation.m
function bw =image_segmentation(I)  %图像分割
Image = I;              %读取RGB图像
Image=im2double(Image); %双精度类型 便于运算
I=rgb2hsv(Image);       %RGB模型转换hsv模型
[y,x,z]=size(I);        %%y x z 返回RGB彩色图像数据矩阵行 列 等
Blue_y = zeros(y, 1);  
% p=[0.56 0.71 0.4 1 0.3 1 0];  %蓝色
p=[0.2 0.42 0.1 1 0.3 1 0]; %绿色
for i = 1 : y  
    for j = 1 : x  
        hij = I(i, j, 1);  
        sij = I(i, j, 2);  
        vij = I(i, j, 3);  
        if (hij>=p(1) && hij<=p(2)) &&( sij >=p(3)&& sij<=p(4))&&...  
                (vij>=p(5)&&vij<=p(6))  
            Blue_y(i, 1) = Blue_y(i, 1) + 1;  %蓝色像素点统计 
        end  
    end  
end  
[~, MaxY] = max(Blue_y);  %最大值 
Th = p(7);  
PY1 = MaxY;  
while ((Blue_y(PY1,1)>Th) && (PY1>0))  
    PY1 = PY1 - 1;  
end  
PY2 = MaxY;  
while ((Blue_y(PY2,1)>Th) && (PY2 y  
    PY2 = y;  
end  
bw=Image(PY1:PY2,:,:); 
IY = I(PY1:PY2, :, :);   
I2=im2bw(IY,0.5);  
  
[y1,x1,z1]=size(IY);  
Blue_x=zeros(1,x1);  
for j = 1 : x1  
    for i = 1 : y1  
        hij = IY(i, j, 1);  
        sij = IY(i, j, 2);  
        vij = IY(i, j, 3);  
        if (hij>=p(1) && hij<=p(2)) &&( sij >=p(3)&& sij<=p(4))&&...  
                (vij>=p(5)&&vij<=p(6))  
            Blue_x(1, j) = Blue_x(1, j) + 1;   
%              bw1(i, j) = 1;  
        end  
    end  
end  
PY1;PY2;
  
[~, MaxX] = max(Blue_x);  
Th = p(7);  
PX1 = MaxX;  
  
while ((Blue_x(1,PX1)>Th) && (PX1>0))  
    PX1 = PX1 - 1;  
end  
PX2 = MaxX;  
while ((Blue_x(1,PX2)>Th) && (PX2=max(max(R)));                 %J记录了倾斜角
angle=90-J;
picture=imrotate(bw,angle,'bilinear','crop'); %返回旋转后的图像矩阵。正数表示逆时针旋转，负数表示顺时针旋转。
figure('NumberTitle','off','Name','倾斜校正图像');
imshow(picture);title('倾斜校正');
imwrite(picture,'倾斜校正车牌.jpg');
end

%% 形态学函数xingtaixue.m
function picture_6 = xingtaixue(picture_1)
threshold = 5;
picture_2 = im2bw(picture_1,graythresh(picture_1)); %最大类间方差法 图像二值化
picture_2=imcomplement(picture_2);%求二值图像的补，赋值给picture_2
figure('NumberTitle','off','Name','车牌二值化'),imshow(picture_2);title('二值化');
picture_3 = bwmorph(picture_2,'hbreak',inf); %对二值图像的形态学操作 移除H连通的像素
picture_4 = bwmorph(picture_3,'spur',inf); %删除杂散像素
picture_5 = bwmorph(picture_4,'open',inf); %执行形态学开运算（先腐蚀后膨胀）
picture_6 = bwareaopen(picture_5,threshold); %移除小于threshold的部分
picture_6 = ~picture_6;
figure('NumberTitle','off','Name','形态学操作'),imshow(picture_6);title('形态学操作'); 
end

%% 图像裁剪函数caijian.m
function bw = caijian(picture_6)
threshold =5 ;
picture_7=touying(picture_6);
picture_8=~picture_7;
picture_9 = bwareaopen(picture_8, threshold);
picture_10=~picture_9;
[y,x]=size(picture_10);%对长宽重新赋值%1为白色
bw = picture_10;
[y,x] = size(bw);
dd = fix(x/40);
ddd = fix(x/30);
dd = x - dd;
bw = bw(:,ddd:dd);
figure('NumberTitle','off','Name','边框去除'),imshow(bw),title('边框去除');  
end

%% 文字切割qiege.m
function image=qiege(bw) 
[y,x] = size(bw);
bw(:,x)=1;
bw(:,1)=1;
a = sum(~bw);
figure('NumberTitle','off','Name','投影'),bar(a),title('投影');
j = 1;
jj = 1;
m =0;
for i = 1:x-1
    if a(i)==0 && a(i+1)~=0
        j = i;
    end
    if a(i)~=0 && a(i+1)==0
        kk=i;
    else
        kk =0;
    end
    if kk~=0
        m = m+1;
        p(m) = j; %字起始横坐标
        q(m) = kk; %字结束横坐标
    end    
end

for i = 1:m
    if p(i)(fix(x/20))
        gg(k) = q(i);
        ggg(k) = p(i);
        k = k+1;
    end
end
 
figure('NumberTitle','off','Name','字符分割'),
k =1;
p = zeros(110,55);
image = {p p p p p p p};
for ii = 1:8
    p = imresize(bw(:,ggg(ii):gg(ii)), [110 55],'bilinear');
    image{ii} = mat2cell(p,[110 0],[55 0]);
    obj = subplot(1,8,ii); imshow(p),title(obj,ii);pause(0.2);
    k = k +1;
end
end

%% 字符识别函数 zifu_shibie.m
function bb =zifu_shibie(image)
liccode=char(['0':'9' 'A':'Z' '贵桂沪京鲁陕苏渝豫粤']); %建立自动识别字符代码表 
for ii=1:8
    tu = double(cell2mat(image{ii}));
    if ii==1                 %第一位汉字识别
        kmin=37;
        kmax=46;
    elseif ii==2             %第二位 A~Z 字母识别
        kmin=11;
        kmax=36;
    elseif ii>=3
        kmin=1;
        kmax=36; 
    end
     k = 1;
    for k1 = kmin:kmax
        k2 = k1-kmin+1;
        fname=strcat('字符模板\',liccode(k1),'.bmp');
        picture = imread(fname);
        bw(:,:,k2) = imresize(im2bw(picture,graythresh(rgb2gray(picture))),[110 55],'bilinear');
        [y,x,z]=size(tu);
        sum =0;
        for i=1:y
            for j=1:x
                if  tu(i,j)==bw(i,j,k2)%统计黑白
                    sum=sum+1;
                end
            end
        end
        baifenbi(1,k)=sum/(160*55);
        k = k+1;
    end
    chepai= find(baifenbi>=max(baifenbi));
    jj =kmin+chepai-1;
    bb(ii) =' ';
    bb(ii)  = liccode(jj);
end
figure('NumberTitle','off','Name','车牌号码'),title (['识别车牌号码:', bb],'Color','r');
end

%% 获取字符函数 getword.m
function [word,result]=getword(d)
word=[];flag=0;y1=8;y2=0.5;
    while flag==0
        [m,n]=size(d);
        wide=0;
        while sum(d(:,wide+1))~=0 && wide<=n-2
            wide=wide+1;
        end
        temp=qiege(imcrop(d,[1 1 wide m]));
        [m1,n1]=size(temp);
        if widey2
            d(:,[1:wide])=0;
            if sum(sum(d))~=0
                d=qiege(d);  % 切割出最小范围
            else word=[];flag=1;
            end
        else
            word=qiege(imcrop(d,[1 1 wide m]));
            d(:,[1:wide])=0;
            if sum(sum(d))~=0;
                d=qiege(d);flag=1;
            else d=[];
              end
           end
        end
          result=d;
end
          
%% 图像投影函数touying.m
function bw_fir = touying(imane_bw)
X_yuzhi=1;
[y,x]=size(imane_bw);
Y_touying=(sum((~imane_bw)'))';%往左边投影统计黑点
X_touying=sum((~imane_bw));%往下面投影
%找黑体边缘
Y_up=fix(y/2);
Y_yuzhi=mean(Y_touying((fix(y/2)-10):(fix(y/2)+10),1))/1.6;
while ((Y_touying(Y_up,1)>=Y_yuzhi)&&(Y_up>1))%找到图片上边界  
       Y_up=Y_up-1;
end   
Y_down=fix(y/2);
while ((Y_touying(Y_down,1)>=Y_yuzhi)&&(Y_down>>>>>>>');
step=steps/100;
for k=1:steps
    if steps-k<=5
        waitbar(k/steps,hwait,'即将完成');
        pause(0.05);
    else
        PerStr=fix(k/step);
        str=['正在运行中',num2str(PerStr),'%'];
        waitbar(k/steps,hwait,str);
        pause(0.05);
    end
end
close(hwait);
end

二、路径规划

路径规划部分在无人车架构体系当中分属控制或决策部分，是实现自动充电车的关键技术之一。路径规划模块性能的高低直接关系车辆行驶路径选择的优劣和行驶的流畅度，而路径规划算法的性能优劣很大程度上取决于规划算法的优劣。如何在各种场景下迅速、准确地规划出一条高效路径且使其具备应对场景动态变化的能力是路径规划算法应当解决的问题。

1. 路径规划分类

根据对环境信息的把握程度可把路径规划划分为基于环境先验完全信息的全局路径规划和基于传感器信息的局部路径规划。其中，从获取障碍物信息是静态或是动态的角度看，全局路径规划属于静态规划，局部路径规划属于动态规划。全局路径规划需要掌握所有的环境信息，根据环境地图的所有信息进行路径规划；局部路径规划只需要由传感器实时采集环境信息，了解环境地图信息，然后确定出所在地图的位置及其局部的障碍物分布情况，从而可以选出从当前结点到某一子目标结点的最优路径。

移动机器人的路径规划方法主要分为基于搜索的路径规划算法、基于采样的路径规划算法、智能仿生算法和基于势场的路径规划算法。图9展示了不同方式各自的几种经典算法。

按照大体思路不同还可以分为图像搜索和势场规划两大类。图像搜索首先构造自由空间中的连接图，然后搜索达到目标；势场规划是在空间中直接加入数学函数，然后跟踪该函数的梯度达到目标。

图9 路径规划分类

基于搜索的路径规划算法，包括Dijkstra、A*、D*、 LPA*和D* Lite等。

Dijkstra算法是由E.W.Dijkstra于1959年提出，又叫迪杰斯特拉算法。该算法采用了一种贪心模式，其解决的是有向图中单个节点到另一节点的最短路径问题，其主要特点是每次迭代时选择的下一个节点是当前节点最近的子节点，也就是说每一次迭代行进的路程是最短的。

A*算法是启发式搜索算法，启发式搜索即在搜索过程中建立启发式搜索规则，以此来衡量实时搜索位置和目标位置的距离关系，使搜索方向优先朝向目标点所处位置的方向，最终达到提高搜索效率的效果。A*的算法的基本思想如下：引入当前节点x的估计函数f(x)，当前节点x的估计函数定义为：

f(x) = g(x) + h(x)

其中g(x)是从起点到当前节点x的实际距离量度，h(x)是从节点x到终点的最小距离。算法基本实现过程为：从起始点开始计算其每一个子节点的f值，从中选择f值最小的子节点作为搜索的下一点，往复迭代，直到下一子节点为目标点。

D*算法是一种反向增量式搜索算法，反向即算法从目标点开始向起点逐步搜索；增量式搜索，即算法在搜索过程中会计算每一个节点的距离度量信息H(x)，在动态环境中若出现障碍物无法继续沿预先路径搜索，算法会根据原先已经得到的每个点的距离度量信息在当前状态点进行路径再规划，无需从目标点进行重新规划。

LPA*算法的搜索起始点为所设起点（正向搜索），按照Key值的大小作为搜索前进的原则，迭代到目标点为下一搜索点时完成规划；Key值中包含启发式函数h项作为启发原则来影响搜索方向；处于动态环境时，LPA*可以适应环境中障碍物的变化而无需重新计算整个环境，方法是在当前搜索期间二次利用先前搜索得到的g值，以便重新规划路径。

D* Lite算法是Koenig S和Likhachev M基于LPA*算法基础上提出的路径规划算法。D* Lite与LPA*的主要区别在于搜索方向的不同，是将Key定义中涉及到的目标点goal替换为起始点start的相应信息。D* Lite算法是先在给定的地图集中逆向搜索并找到一条最优路径。在其接近目标点的过程中，通过在局部范围的搜索去应对动态障碍点的出现。增量式算法的优势在于：各个点的路径搜索己经完成，在遇到障碍点无法继续按照原路径进行逼近时，通过增量搜索的数据再利用直接在受阻碍的当前位置重新规划岀一条最优路径，然后继续前进。

以上五种算法的区别如表2所示。

表2 算法比较

算法	搜索方向	启发式	增量式	适用范围	现实应用
Dijkstra	正向搜索	否	否	全局信息已知，静态规划	网络通信中的最短路由选择
A*	正向搜索	是	否	全局信息已知，静态规划	Apollo、游戏、无人机路径规划
D*	反向搜索	否	是	部分信息已知，静态规划	机器人探路、火星探测车路径规划
LPA*	反向搜索	否	是	部分信息已知，假设其余为自由通路，动态规划	机器人路径规划
D* Lite	反向搜索	是	是	部分信息已知，假设其余为自由通路，动态规划	机器人路径规划

2. 路径规划实现

针对全局信息已知的停车场路径规划问题，这里我们使用A*算法来完成充电车从起点到终点的路径规划。较于传统的A*算法，我们优化其中一些地方，将其改良为动态衡量式的A*算法。在初始参数设定中添加h(x)的权重系数Weights，亦即将原本代价计算公式f(x) = g(x) + h(x)变成f(x) = g(x) + w(x)*h(x),其中w(x)>=1。在搜索过程中，可以通过改变w(x)来影响搜索过程h(x)对A*算法的影响；在实际应用中，可以灵活调整Weights的值以改变运行速度和准确率。如果将Weights设为0，动态衡量式的A*算法就变成了Dijkstra算法，而当Weights设置较大时，则可以将该算法当作BFS算法使用。在一般的路径规划算法中，不注重规划路径中存在的转弯问题。因为我们的最终目标是控制充电车移动，所以需要尽量减少转弯的次数，对此增加功能函数Corner_amend，选择是否进行拐角的修正。

本项目中编写的路径规划程序流程如下：

（1）设定功能参数。分别设置图片中代表停车场大小的方格数、动态衡量启发式A*算法中h(x)的权重系数、两次识别车辆的初始值等。

（2）设计车位。按照传统停车场车位安排规律，设计如图10所示的简易车位布局方案。

图10 简易车位布局

 

（3）创建方格及障碍物。使用编写的initializeField函数按照上图所示方格和障碍物（车位）绘图。

（4）初始化矩阵和变量。

（5）生成方格和障碍物图像。使用编写的createFigure函数生成环境、障碍物、起点和终点。结果如图11所示，其中（1，1）处绿圈为起点，（11，17）处黄色方块为终点。

图11 生成方格和障碍物

（6）给车位标号。

（7）利用循环迭代找到终止点路径。主要步骤包括初始化矩阵，调用findValue函数进行点的拓展，从setOpen（表示已经拓展出来的点）中删除放到矩阵setClosed（存放setOpen中最优的值）中的点，把拓展出来的点中符合要求的点放到setOpen矩阵中，作为待选点等。

（8）路径回溯并绘制路径曲线。从终点往前依次寻找是由哪个点拓展出来的，即寻找父节点。这样不断回溯直至到起始点，然后将找到的父节点存到矩阵p中，并根据p中数据绘制路径曲线。结果如图12所示。

图12 路径图

（9）识别车牌和车尾方向。调用之前编写的车牌识别函数，自动识别充电车摄像头获得的车牌图片，将结果与APP中输入的车牌号进行比对，如果号码符合则再根据车尾朝向决定充电车最终充电地点；若不符合则输出-1并回到原点。

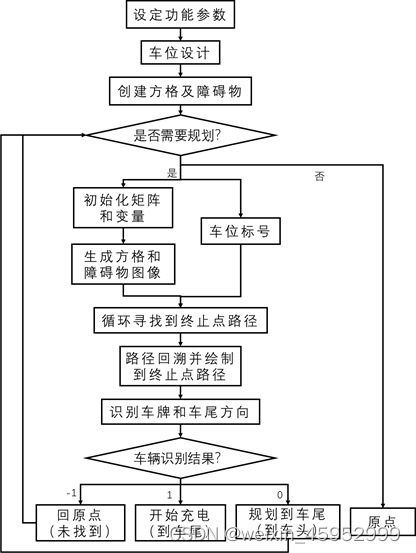
综上所述，车辆具体的实施流程如图13所示。

 图13 程序流程图

路径规划程序如下所示。

% 初始化
clc;             %清除命令窗口的内容
clear all;       %清除工作空间的所有变量，函数，和MEX文件
close all;       %关闭所有的figure窗口

[y,Fs] = audioread('001.wav'); sound(y,Fs); % 播放名为001的音乐

%功能参数的设定部分
n = 30;   % 产生一个n x n的方格，修改此值可以修改生成图片的方格数
% wallpercent = 0.4;  % 这个变量代表生成的障碍物占总方格数的比例 ，如0.5 表示障碍物占总格数的50%
Weights=1;       %动态衡量启发式A星算法中的h（n）权重系数
Corner_amend=1;  %选择是否进行拐角的修正，该变量设为0则不进行拐角修正，设为1则进行拐角修正
find_or_not=1; %第一次是否找到，未找到为0
find_or_not2 = 0; %第二次是否找到，初始为0

%车位设计
block=[1,2,3,4,5];
rows=[block+1,block+7,block+14,block+20,[28,29,30]]; %车位纵坐标
col=[2,3, 6,7,9,10, 13,14,16,17, 21,22,24,25, 28,29]; %车位横坐标
coln=[2,6,9,13,16,21,24,28]; % 标号横坐标
count=1;
database=[]; %存储车位序号及坐标
database_flip=[]; %存储车位方向错误时的序号和坐标
for posi_x=coln
     for posi_y=rows
     if mod(count/23,2)<=1
         database=[database;count,posi_y,posi_x+2];
         database_flip=[database_flip;count,posi_y,posi_x-1];
     else 
         database=[database;count,posi_y,posi_x-1];
         database_flip=[database_flip;count,posi_y,posi_x+2];
     end
     count=count+1;
     end
end

% 方格以及障碍物的创建
[field, startposind, goalposind, costchart, fieldpointers,endnum] =initializeField(n,rows,col,database); %随机生成包含障碍物，起始点，终止点等信息的矩阵

% 车牌号
prompt='请输入车牌号： ';
plate_num=input(prompt,'s')

flag=true; %控制路径规划的终止
while flag
    % 路径规划中用到的一些矩阵的初始化
    setOpen = [startposind]; setOpenCosts = [0]; setOpenHeuristics = [Inf];
    setClosed = []; setClosedCosts = [];
    movementdirections = {'R','L','D','U'};  %移动方向
    % 初始化一些进行路径的修正需要用到的变量
    Parent_node=0; %Parent_node初始化，否则会报错
    Expected_note=0;%Expected_note初始化，否则会报错
    untext_ii=0;  %未经过检验的新的ii
    amend_count=0;% 记录修正的次数
    
    % 这个函数用来生成环境，障碍物，起点，终点
    axishandle = createFigure(field,costchart,startposind,goalposind);    %将生成的方格及障碍物的数据生成图像
    
    % 给车位标号
    count=1;
    for posi_x=coln
        for posi_y=rows
            text(posi_x+.5,posi_y+.5,num2str(count),'color','red');
            count=count+1;
        end
    end
    
    %%
    % 这个while循环是本程序的核心，利用循环进行迭代来寻找终止点
    while ~max(ismember(setOpen,goalposind)) && ~isempty(setOpen)
        [temp, ii] = min(setOpenCosts +Weights*setOpenHeuristics);     %寻找拓展出来的最小值 
        if ((setOpen(ii)~=startposind) && (Corner_amend==1))
            [new_ii,amend_count_1]=Path_optimization(temp, ii,fieldpointers,setOpen,setOpenCosts,startposind,Weights,setOpenHeuristics,Parent_node,Expected_note,untext_ii,amend_count); %进行路径的修正，在保证不增加距离的基础上，使其减少转弯的次数
            ii=new_ii;
            amend_count=amend_count_1;
        end
        
        %这个函数的作用就是把输入的点作为父节点，然后进行拓展找到子节点，并且找到子节点的代价，并且把子节点距离终点的代价找到
        [costs,heuristics,posinds] = findFValue(setOpen(ii),setOpenCosts(ii), field,goalposind,'euclidean');
        setClosed = [setClosed; setOpen(ii)];     % 将找出来的拓展出来的点中代价最小的那个点串到矩阵setClosed 中 
        setClosedCosts = [setClosedCosts; setOpenCosts(ii)];    % 将拓展出来的点中代价最小的那个点的代价串到矩阵setClosedCosts 中
        % 从setOpen中删除刚才放到矩阵setClosed中的那个点
        %如果这个点位于矩阵的内部
        if (ii > 1 && ii < length(setOpen))
            setOpen = [setOpen(1:ii-1); setOpen(ii+1:end)];
            setOpenCosts = [setOpenCosts(1:ii-1); setOpenCosts(ii+1:end)];
            setOpenHeuristics = [setOpenHeuristics(1:ii-1); setOpenHeuristics(ii+1:end)];

        %如果这个点位于矩阵第一行
        elseif (ii == 1)
            setOpen = setOpen(2:end);
            setOpenCosts = setOpenCosts(2:end);
            setOpenHeuristics = setOpenHeuristics(2:end);

        %如果这个点位于矩阵的最后一行
        else
            setOpen = setOpen(1:end-1);
            setOpenCosts = setOpenCosts(1:end-1);
            setOpenHeuristics = setOpenHeuristics(1:end-1);
        end
        
        %%
        % 把拓展出来的点中符合要求的点放到setOpen 矩阵中，作为待选点
        for jj=1:length(posinds)
            if ~isinf(costs(jj))   % 判断该点（方格）处没有障碍物
                % 判断一下该点是否 已经存在于setOpen 矩阵或者setClosed 矩阵中
                % 如果我们要处理的拓展点既不在setOpen 矩阵，也不在setClosed 矩阵中
                if ~max([setClosed; setOpen] == posinds(jj))
                    fieldpointers(posinds(jj)) = movementdirections(jj);
                    costchart(posinds(jj)) = costs(jj);
                    setOpen = [setOpen; posinds(jj)];
                    setOpenCosts = [setOpenCosts; costs(jj)];
                    setOpenHeuristics = [setOpenHeuristics; heuristics(jj)];
                    
                % 如果我们要处理的拓展点已经在setOpen 矩阵中
                elseif max(setOpen == posinds(jj))
                    I = find(setOpen == posinds(jj));
                    % 如果通过目前的方法找到的这个点，比之前的方法好（代价小）就更新这个点
                    if setOpenCosts(I) > costs(jj)
                        costchart(setOpen(I)) = costs(jj);
                        setOpenCosts(I) = costs(jj);
                        setOpenHeuristics(I) = heuristics(jj);
                        fieldpointers(setOpen(I)) = movementdirections(jj);
                    end
                % 如果我们要处理的拓展点已经在setClosed 矩阵中
                else
                    I = find(setClosed == posinds(jj));
                    % 如果通过目前的方法找到的这个点，比之前的方法好（代价小）就更新这个点
                    if setClosedCosts(I) > costs(jj)
                        costchart(setClosed(I)) = costs(jj);
                        setClosedCosts(I) = costs(jj);
                        fieldpointers(setClosed(I)) = movementdirections(jj);
                    end
                end
            end
        end
        
        %%
        if isempty(setOpen) break; end
        set(axishandle,'CData',[costchart costchart(:,end); costchart(end,:) costchart(end,end)]);
        set(gca,'CLim',[0 1.1*max(costchart(find(costchart < Inf)))]);
        drawnow; 
    end
    
    % 调用findWayBack函数进行路径回溯，并绘制出路径曲线
    if max(ismember(setOpen,goalposind))
        disp('Solution found!');
        p = findWayBack(goalposind,fieldpointers); % 调用findWayBack函数进行路径回溯，将回溯结果放于矩阵P中
        plot(p(:,2)+0.5,p(:,1)+0.5,'Color',0.2*ones(3,1),'LineWidth',4);  %用 plot函数绘制路径曲线
        drawnow;
        drawnow;
        clear sound
        [y,Fs] = audioread('002.wav'); sound(y,Fs); % 播放名为000的音乐
    elseif isempty(setOpen)
        disp('No Solution!'); 
        clear sound
        [y,Fs] = audioread('000.wav'); 
        sound(y,Fs);
    end
    
    %识别车牌是否与输入相同，如果相同再判断是车头还是车尾，最后根据结果选择是否重复循环
    if (find_or_not==1) && (find_or_not2 == 0)
        [plate_num_str]=number_plate();
        if strcmp(plate_num_str,plate_num)==0 % 输入车牌号与识别到的不同
            judgement=-1;
        else  % 输入车牌号与识别到的相同
            prompt_judge = '是否为车尾？车尾为1，车头为0 :  ';
            judgement = input(prompt_judge);
        end
    end
    
    if (judgement == 1) || (find_or_not2 == 1) ||(find_or_not == 0)
        flag=false;
    elseif judgement == -1 %未找到车
        startposind = goalposind;
        goalposind = 1;
        fieldpointers = cell(n,n);%生成元胞数组n*n
        fieldpointers(:)= {'1'};
        fieldpointers{startposind} = 'S'; fieldpointers{goalposind} = 'G'; %将元胞数组的起始点的位置处设为 'S'，终止点处设为'G'
        fieldpointers(field==inf)={'0'};
        find_or_not = 0;
    else
        startposind = goalposind;
        goalposind = sub2ind([n,n],database_flip(endnum,2),database_flip(endnum,3));
        fieldpointers = cell(n,n);%生成元胞数组n*n
        fieldpointers(:)= {'1'};
        fieldpointers{startposind} = 'S'; fieldpointers{goalposind} = 'G'; %将元胞数组的起始点的位置处设为 'S'，终止点处设为'G'
        fieldpointers(field==inf)={'0'};
        find_or_not2 = 1;
    end

end

%% findWayBack函数
%findWayBack函数用来进行路径回溯，这个函数的输入参数是终止点goalposind和矩阵fieldpointers，输出参数是P
function p = findWayBack(goalposind,fieldpointers)

    n = length(fieldpointers);  % 获取环境的长度也就是n
    posind = goalposind;
    [py,px] = ind2sub([n,n],posind); % 将索引值posind转换为坐标值 [py,px]
    p = [py px];
    
    %利用while循环进行回溯，当我们回溯到起始点的时候停止，也就是在矩阵fieldpointers中找到S时停止
    while ~strcmp(fieldpointers{posind},'S')
      switch fieldpointers{posind}
          
        case 'L' % ’L’ 表示当前的点是由左边的点拓展出来的
          px = px - 1;
        case 'R' % ’R’ 表示当前的点是由右边的点拓展出来的
          px = px + 1;
        case 'U' % ’U’ 表示当前的点是由上面的点拓展出来的
          py = py - 1;
        case 'D' % ’D’ 表示当前的点是由下边的点拓展出来的
          py = py + 1;
      end
      p = [p; py px];
      posind = sub2ind([n n],py,px);% 将坐标值转换为索引值
    end
end

%% findFValue函数
%这个函数的作用就是把输入的点作为父节点，然后进行拓展找到子节点，并且找到子节点的代价，并且把子节点距离终点的代价找到。
%函数的输出量中costs表示拓展的子节点到起始点的代价，heuristics表示拓展出来的点到终止点的距离大约是多少，posinds表示拓展出来的子节点
function [cost,heuristic,posinds] = findFValue(posind,costsofar,field,goalind,heuristicmethod)
    n = length(field);  % 获取矩阵的长度
    [currentpos(1) currentpos(2)] = ind2sub([n n],posind);   %将要进行拓展的点（也就是父节点）的索引值拓展成坐标值
    [goalpos(1) goalpos(2)] = ind2sub([n n],goalind);        %将终止点的索引值拓展成坐标值
    cost = Inf*ones(4,1); heuristic = Inf*ones(4,1); pos = ones(4,2); %将矩阵cost和heuristic初始化为4x1的无穷大值的矩阵，pos初始化为4x2的值为1的矩阵
    
    % 拓展方向一
    newx = currentpos(2) - 1; newy = currentpos(1);
    if newx > 0
      pos(1,:) = [newy newx];
      switch lower(heuristicmethod)
        case 'euclidean'
          heuristic(1) = 10*abs(goalpos(2)-newx) + 10*abs(goalpos(1)-newy);
        case 'taxicab'
          heuristic(1) = 10*abs(goalpos(2)-newx) +10*abs(goalpos(1)-newy);
      end
      cost(1) = costsofar + field(newy,newx);
    end

    % 拓展方向二
    newx = currentpos(2) + 1; newy = currentpos(1);
    if newx <= n
      pos(2,:) = [newy newx];
      switch lower(heuristicmethod)
        case 'euclidean'
          heuristic(2) = 10*abs(goalpos(2)-newx) +10*abs(goalpos(1)-newy);
        case 'taxicab'
          heuristic(2) = 10*abs(goalpos(2)-newx) + 10*abs(goalpos(1)-newy);
      end
      cost(2) = costsofar + field(newy,newx);
    end

    % 拓展方向三
    newx = currentpos(2); newy = currentpos(1)-1;
    if newy > 0
      pos(3,:) = [newy newx];
      switch lower(heuristicmethod)
        case 'euclidean'
          heuristic(3) = 10*abs(goalpos(2)-newx) + 10*abs(goalpos(1)-newy);
        case 'taxicab'
          heuristic(3) = 10*abs(goalpos(2)-newx) + 10*abs(goalpos(1)-newy);
      end
      cost(3) = costsofar + field(newy,newx);
    end

    % 拓展方向四
    newx = currentpos(2); newy = currentpos(1)+1;
    if newy <= n
      pos(4,:) = [newy newx];
      switch lower(heuristicmethod)
        case 'euclidean'
          heuristic(4) = 10*abs(goalpos(2)-newx) + 10*abs(goalpos(1)-newy);
        case 'taxicab'
          heuristic(4) = 10*abs(goalpos(2)-newx) + 10*abs(goalpos(1)-newy);
      end
      cost(4) = costsofar + field(newy,newx);
    end
     posinds = sub2ind([n n],pos(:,1),pos(:,2)); % 将拓展出来的子节点的坐标值转换为索引值
end

%%  initialize field
%这个矩阵的作用就是随机生成环境，障碍物，起始点，终止点等
function [field, startposind, goalposind, costchart, fieldpointers,endnum] = initializeField(n,rows,col,database)
    field = 10*ones(n,n);%设置任意两方格间的距离为10
    
    l1=reshape((rows'.*ones(1,length(col)))',1,[]);
    l2=repmat(col,1,length(rows));
    field(sub2ind([n n],l1,l2)) = Inf;%向上取整
    
    %起始点
    prompt1 = '请以数组形式输入起始点坐标: ';
    startp = input(prompt1)
    startposind = sub2ind([n,n],startp(1),startp(2));
    
    %目标点
    prompt2 = '请输入车位号(1-184): ';
    endnum = input(prompt2)
    goalposind = sub2ind([n,n],database(endnum,2),database(endnum,3));
    
    % 随机生成起始点和终止点
%     startposind = sub2ind([n,n],ceil(n.*rand),ceil(n.*rand));  %随机生成起始点的索引值
%     goalposind = sub2ind([n,n],ceil(n.*rand),ceil(n.*rand));   %随机生成终止点的索引值
    field(startposind) = 0; field(goalposind) = 0;  %把矩阵中起始点和终止点处的值设为0
    
    costchart = NaN*ones(n,n);%生成一个nxn的矩阵costchart，每个元素都设为NaN。就是矩阵初始NaN无效数据
    costchart(startposind) = 0;%在矩阵costchart中将起始点位置处的值设为0
    
    % 生成元胞数组
    fieldpointers = cell(n,n);%生成元胞数组n*n
    fieldpointers(:)= {'1'};
    fieldpointers{startposind} = 'S'; fieldpointers{goalposind} = 'G'; %将元胞数组的起始点的位置处设为 'S'，终止点处设为'G'
    fieldpointers(field==inf)={'0'};
     
end
% end of this function

%% createFigure函数
%利用生成的环境数据来进行环境的绘制
function axishandle = createFigure(field,costchart,startposind,goalposind)

      % 这个if..else结构的作用是判断如果没有打开的figure图，则按照相关设置创建一个figure图
      if isempty(gcbf)                                       %gcbf是当前返回图像的句柄，isempty(gcbf)假如gcbf为空的话，返回的值是1，假如gcbf为非空的话，返回的值是0
      figure('Position',[560 70 700 700], 'MenuBar','none');  %对创建的figure图像进行设置，设置其距离屏幕左侧的距离为450，距离屏幕下方的距离为50，长度和宽度都为700，并且关闭图像的菜单栏
      axes('position', [0.01 0.01 0.99 0.99]);               %设置坐标轴的位置，左下角的坐标设为0.01,0.01   右上角的坐标设为0.99 0.99  （可以认为figure图的左下角坐标为0 0   ，右上角坐标为1 1 ）
      else
      gcf; cla;   %gcf 返回当前 Figure 对象的句柄值，然后利用cla语句来清除它
      end
      
      n = length(field);  %获取矩阵的长度，并赋值给变量n
      field(field < Inf) = 0; %将fieid矩阵中的随机数（也就是没有障碍物的位置处）设为0
      pcolor(1:n+1,1:n+1,[field field(:,end); field(end,:) field(end,end)]);%多加了一个重复的（由n X n变为 n+1 X n+1 ）
 
      cmap = flipud(colormap('jet'));  %生成的cmap是一个256X3的矩阵，每一行的3个值都为0-1之间数，分别代表颜色组成的rgb值
      cmap(1,:) = [0.2;0.2;0.2]; cmap(end,:) = ones(3,1); %将矩阵cmap的第一行设为0 ，最后一行设为1
      colormap(flipud(cmap)); %进行颜色的倒转 
      hold on;
      axishandle = pcolor([1:n+1],[1:n+1],[costchart costchart(:,end); costchart(end,:) costchart(end,end)]);  %将矩阵costchart进行拓展，插值着色后赋给axishandle
      [goalposy,goalposx] = ind2sub([n,n],goalposind);
      [startposy,startposx] = ind2sub([n,n],startposind);
       plot(goalposx+0.5,goalposy+0.5,'ys','MarkerSize',10,'LineWidth',6);
       plot(startposx+0.5,startposy+0.5,'go','MarkerSize',10,'LineWidth',6);
       %uicontrol('Style','pushbutton','String','RE-DO', 'FontSize',12, 'Position', [1 1 60 40], 'Callback','astardemo');
end
%%
function [new_ii,amend_count_1] = Path_optimization(temp, ii,fieldpointers,setOpen,setOpenCosts,startposind,Weights,setOpenHeuristics,Parent_node,Expected_note,untext_ii,amend_count)
   n = length(fieldpointers);  %获取矩阵的长度，并赋值给变量n
   
 %获取其父节点的索引值
  switch fieldpointers {setOpen(ii)}
        case 'L' % ’L’ 表示当前的点是由左边的点拓展出来的
          Parent_node = setOpen(ii) - n;
        case 'R' % ’R’ 表示当前的点是由右边的点拓展出来的
           Parent_node = setOpen(ii) + n;
        case 'U' % ’U’ 表示当前的点是由上面的点拓展出来的
           Parent_node = setOpen(ii) -1;
        case 'D' % ’D’ 表示当前的点是由下边的点拓展出来的
           Parent_node = setOpen(ii) + 1;          
  end
  
  if Parent_node==startposind  %如果这个点的父节点是起始点的话，跳过修正
     new_ii=ii;
     amend_count_1=amend_count;
  else 
  
       %获取期望下一步要走的点的索引值
     switch fieldpointers{Parent_node}
          
        case 'L' % ’L’ 表示当前的点是由左边的点拓展出来的,走直线的话，我们期望要走的下一个点为此点右边的点
          Expected_note = Parent_node + n;
        case 'R' % ’R’ 表示当前的点是由右边的点拓展出来的，走直线的话，我们期望要走的下一个点为此点左边的点
           Expected_note =  Parent_node - n;
        case 'U' % ’U’ 表示当前的点是由上面的点拓展出来的，走直线的话，我们期望要走的下一个点为此点下面的点
           Expected_note = Parent_node +1;
        case 'D' % ’D’ 表示当前的点是由下边的点拓展出来的，走直线的话，我们期望要走的下一个点为此点上面的点
           Expected_note = Parent_node - 1;
     end
   
     if ((Expected_note<=0)||(Expected_note>n*n))   %如果我们期望的点不在待选点矩阵setOpen中，或者超出边界，跳过修正
          new_ii=ii;
          amend_count_1=amend_count;
     else
           
           %计算新的要进行拓展的点在setOPen中的索引值 
         if fieldpointers{setOpen(ii)}==fieldpointers{Parent_node}   %如果修正之前要走的点就是我们期望的构成直线的点，跳出修正
                new_ii=ii;
                amend_count_1=amend_count;
         elseif  find(setOpen == Expected_note)  %如果我们期望要走的点在待选点矩阵setOpen中
             
                 untext_ii=find(setOpen == Expected_note);
                 now_cost=setOpenCosts(untext_ii) +Weights*setOpenHeuristics(untext_ii);   %计算期望点要花费的代价
                 
                if  temp==now_cost       %如果我们期望的点要花费的代价等于修正之前要走的点花费的代价，就进行修正（因为之前要走的点，是待选点矩阵setOPen中代价最小的一个点之一，所以期望的点的代价不可能小于该点）
                     new_ii=untext_ii;   %将新的setOPen矩阵的索引值赋值给new_ii输出
                     amend_count=amend_count+1;
                     amend_count_1=amend_count; %amend_count_1中记录了我们进行修正的次数，为了查看这个函数是否有发挥作用
                else
                     new_ii=ii;          %如果我们期望的点要花费的代价大于修正之前要走的点花费的代价，就跳过修正（A星算法要保证进行拓展的点是待选点中代价最小的，这也是导致远离终止点的哪一类拐角无法得到修正的原因）
                     amend_count_1=amend_count;
                end
         else
                 new_ii=ii;    %如果我们期望的点不在待选点矩阵setOpen中（也就是这个点是障碍物或者超出边界了），则跳过修正
                 amend_count_1=amend_count;
         end
     end   
  end     
     
end

相关资源链接：识别电动汽车车牌并使用自动充电车充电的方案

路径规划部分的音频随便找三个或者把那部分删除就行，不想上传了。