蚁群算法再优化：combine aco algorithm with Sarsa in RL

蚁群算法、Sarsa介绍和TSP问题介绍

在进行蚁群算法优化介绍之前，笔者先将涉及到的算法等应用背景与大家说清楚。

TSP和Sarsa

TSP问题叫旅行商问题，即给定n个城市和他们的坐标，城市之间的距离表示为dij(i，j分别为不同城市的下标)，d的距离一般用欧式距离，且为对称问题(就是i->j 和 j->i的距离是相等的)，我们要寻找一个哈密顿回路，来使得回路的消耗最小，这就是我们的TSP问题的目标。
Sarsa算法是强化学习中智能体在未知空间学习策略的一种经典算法。其大致思路是智能体（agent）下一时刻采取的动作参考动作所带来的收益，且以ε的概率采取获得收益的最大动作，1-ε的概率随机选取剩下的动作进行寻优。
具体的相关的文章可以参看笔者之前的blog，强化学习的Sarsa与Q-Learning的Cliff-Walking对比实验.下面引用文章中Sarsa的伪代码。

aco algorithm

蚁群算法是一种仿生的启发式算法，也是经典的启发式算法之一。提出多年来有不少学者在研究蚁群并进行改进，很多算法会将蚁群算法和其他启发式算法结合起来，或者和现在流行的深度学习，强化学习结合，从而产生寻优能力更加强大的算法。当然经典的蚁群算法在解决TSP问题中的效果已经远不如最好的方法，但是从基础小部分研究改进起，才能构建好高楼大厦。这也是文章的目的。
蚁群算法根据之前蚂蚁留下的信息素来决定接下来将要走的道路，直到到达目的地，也就是著名的蚂蚁效应。该思路被用来设计成ACO，在TSP问题中进行了应用。下面是蚁群算法的流程图

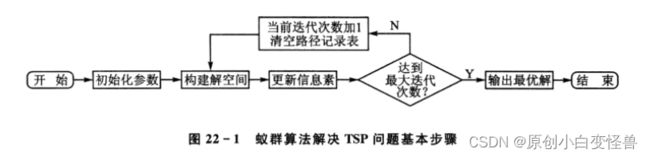
具体的改进和代码

改进说明

以一定概率rr（用伪随机数），当rr>0.1时，选最大的下一个城市，来进行城市回路的构建
以1-ε的概率选择3个最好的下一个城市中的一个
改进的原因：

 引用了Sarsa的思路进行探索
 且探索的是较好的那几个城市中一个
 不是所有城市是因为，最优解的边不会太差，所以不是选取所有的边进行等概率的选择

全部的代码，笔者已经上传到了CSDN中，有需要的可以下载实验
蚁群算法改进

部分代码

下面是根据原来的蚁群算法中，进行改进的部分，其他与原来的一致

        if rr > 0.1:
            for i, probability in enumerate(probabilities):
                rand -= probability
                if rand <= 0:
                    selected = i
                    break
        else:
            sorted_allowed = sorted(enumerate(probabilities), key=lambda x: x[1],reverse=True)
            ex_allowed = sorted_allowed[:2]
            selected = random.choice([tup[0] for tup in ex_allowed])
            while probabilities[selected] == 0:
                selected = random.choice([tup[0] for tup in ex_allowed])

图取自参考文献【1】

数值实验

笔者经过在TSP的公开测试机att48上进行实验证明，经过调参和参数的确定，在进行了1000次的总体实验中，进行数据的收集和总结，最后证明该改进是有效果的，比原来本身的算法取得**1%**的进步。
数据集和代码在签名的代码csdn文件的分享中。
笔者用两组参数进行原蚁群算法和改进蚁群算法的实验，一共4组实验，下面给出参数和实验结果，并进行讨论。
参数的意义分别是，ant数，迭代次数，α，β，衰减率r，固定的Q值 和 选取的计算信息素方式

第一组参数
10, 100, 1.0, 10.0, 0.5, 10, 3
改进的蚁群：ave = 36366      min = 34575
未改进的蚁群：ave = 36536    min=35251


第二组参数
40, 50, 0.1, 18.0, 0.7, 48, 3
改进的蚁群：ave = 35949      min = 34448
未改进的蚁群：ave = 35667    min=34852

结论分析

在参数等控制变量的前提下，改进的蚁群比未改进的最小值要小，注意到第二组参数的改进的ave比没改进的ave高，但是最小值更小，这说明改进的蚁群进行的搜索空间比未改进的更大，所以获得的寻优结果更好。

参考文献

【1】MATLAB智能算法30个案例分析，ISBN：9787512403512，作者：史峰，王辉 等编著