人工智能基础与线性回归模型
文章目录
-
- 1.人工智能、机器学习、深度学习的关系
-
- 1.1 **机器学习**
- 1.2 **深度学习**:是机器学习的其中一种方法,主要原理是**神经网络**
- 1.3 **人工智能与机器学习、深度学习之间的区别**
- 2.机器学习基本概念
- 3.线性回归
-
- 3.1 线性回归模型
-
- 3.1.1 一元线性回归(单个特征)
- 3.1.2 多元线性模型(多个特征)
- 3.2 损失函数
- 3.3 求解方式
-
- 3.3.1 最小二乘法(least square method)
- 3.3.2 梯度下降法(Gradient Descent)
- 3.4 如何评价模型的好坏
- 3.5 **欠拟合与过拟合**
- 4.线性回归实战
-
- 4.1 sklearn介绍
- 4.2 sklearn 数据集
- 4.3 划分数据集
- 4.4 训练模型
-
- 4.4.1 LinearRegression 接口介绍
- 4.4.2 训练模型
- 4.5 评估模型
- 4.6 绘制结果
1.人工智能、机器学习、深度学习的关系
1.1 机器学习
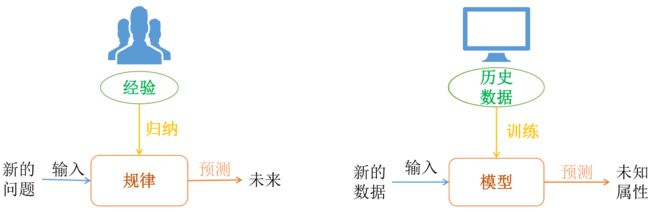
- 目标:让机器具有学习的能力
- 人类解决问题方式:根据已有的数据,归纳总结规律,然后在遇到新的问题时采用归纳总结的规律进行预测
- 机器学习解决问题方式:根据已有的数据(历史数据),选择合适的机器学习算法,构建和训练模型,然后输入新的数据,采用刚刚训练好的模型进行预测结果
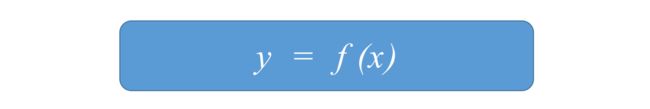
1.2 深度学习:是机器学习的其中一种方法,主要原理是神经网络

我们眼睛看到一张图片,会先提取边缘特征,再识别部件,最后再得到最高层的模式。
1.3 人工智能与机器学习、深度学习之间的区别
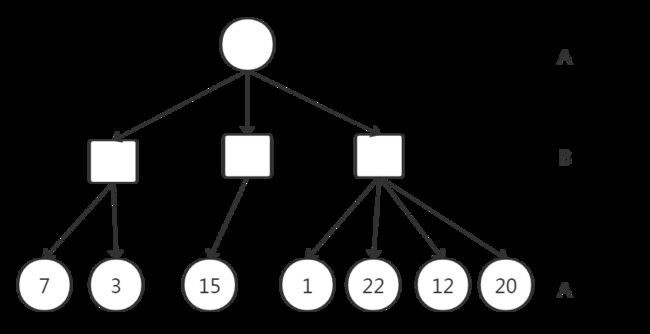
2.机器学习基本概念
- 有监督学习
- 回归
- 分类
- 结构化学习
- 无监督学习
- 如何选择算法
回归:主要用于预测目标值为连续数值型数据。常见场景有股票价格波动的预测,房屋价格的预测等。
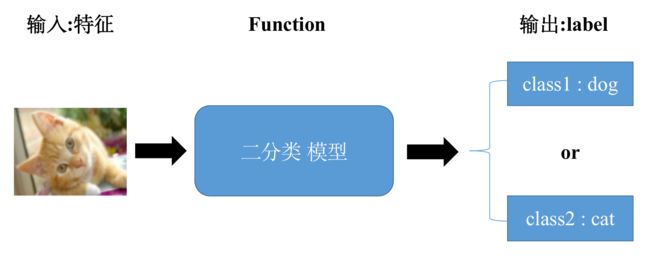
分类:主要将数据划分到合适的类别中。比如将垃圾放入对应的垃圾桶里,湿垃圾放入湿垃圾垃圾桶;常见的应用有猫狗识别(二分类 ),手写数字的识别(多分类)
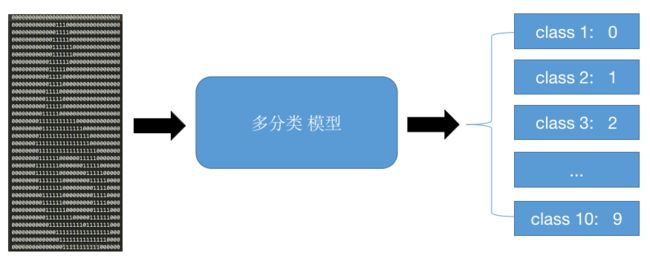
结构化学习:输入输出都是结构化数据
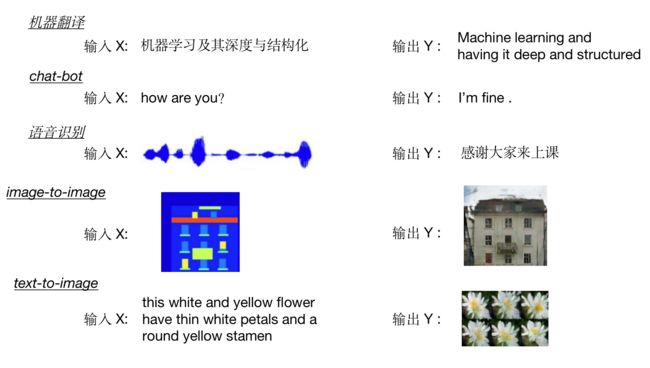
输入输出不是一个标量或者一个类别
一些有结构化数据的输出(比如一个序列、一个句子、一个图等),将输出结构化结果的过程叫做结构化学习或者结构化预测
无监督学习
- 定义:对未标记的样本进行训练学习,比发现这些样本中的结构知识
- 特点: 数据没有类别信息,也不会给定目标值

如何选择算法?

3.线性回归
回归:研究一个或者多个自变量 X 对一个因变量 Y (目标变量)的影响关系情况。
目标变量(Y)为连续数值型,如:房价、人数、降雨量、温度等
回归模型是表示输入变量到输出变量之间映射的函数。
回归问题的学习等价于函数拟合:使用一条函数曲线使其很好的拟合已知数据且能够预测未知数据。
回归问题分为模型的学习和预测两个过程。基于给定的训练数据集构建一个模型,根据新的输入数据预测相应的输出。
3.1 线性回归模型
3.1.1 一元线性回归(单个特征)

那么现在有一个房屋面积为 55平方米,请问最终的租赁价格是多少比较合适?
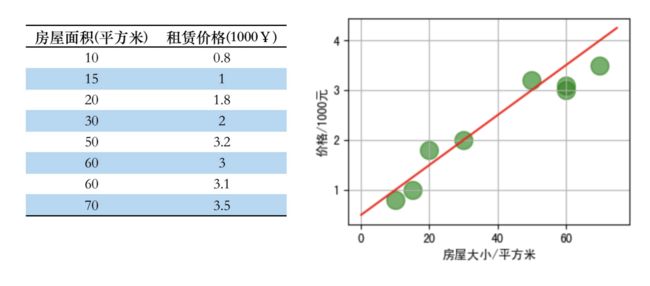
拟合曲线公式(假设函数): y = w x + b y = wx + b y=wx+b
3.1.2 多元线性模型(多个特征)
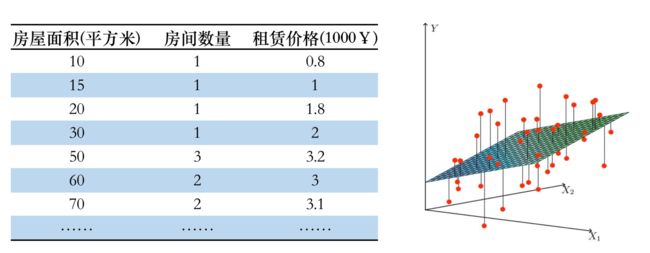
拟合曲线公式: y = b + w 1 x 1 + w 2 x 2 y = b + w_{1}x_{1} + w_{2}x_{2} y=b+w1x1+w2x2
对于 n 维特征(feature)假设函数:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲\begin{split} …
3.2 损失函数
求解最佳参数 w w w,需要一个标准来对结果进行衡量,为此我们需要定量化一个目标函数式,使得计算机可以在求解过程中不断地优化。

针对任何模型求解问题,都是最终都是可以得到一组预测值 y ^ \hat{y} y^ ,对比已有的真实值 y y y,可以将损失函数定义如下:
L ( f ) = ∑ i = 1 n ( y − y ^ ) 2 L(f) = \sum_{i=1}^{n}(y - \hat{y})^2 L(f)=i=1∑n(y−y^)2
即预测值与真实值之间的平均的平方距离,统计中一般称其为MSE(mean square error)均方误差。
损失函数是一个非负实数函数,用来量化模型预测和真实标签之间的差异
将线性回归模型假设函数带入损失函数:
L ( w , b ) = ∑ n = i n [ y i − w x i − b ) ] 2 L(w,b) = \sum_{n=i}^{n}[y_i - wx_i - b)]^2 L(w,b)=n=i∑n[yi−wxi−b)]2
需要求解参数 w 和 b 看作是损失函数 L 的自变量
现在的任务就是求解最小化 L 时 w 和 b 的值,即核心目标优化式为:
( w ∗ , b ∗ ) = arg min ( w , b ) ∑ i = 1 n ( y i − w x i − b ) 2 (w^*,b^*) = \arg \min_{(w,b)} \sum_{i=1}^{n}(y_i - wx_i - b)^2 (w∗,b∗)=arg(w,b)mini=1∑n(yi−wxi−b)2
3.3 求解方式
3.3.1 最小二乘法(least square method)
在统计学中,求解 w 和 b 是使损失函数最小化的过程,称为线性回归模型的最小二乘“参数估计”(parameter estimation)。
L ( w , b ) = ∑ n = i n [ y i − w x i − b ) ] 2 L(w,b) =\sum_{n=i}^{n}[y_i-wx_i-b)]^2 L(w,b)=n=i∑n[yi−wxi−b)]2
我们分别对 w 和 b 求导,得到:
KaTeX parse error: No such environment: equation at position 7: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲\begin{split} …
令上述两式为 0,可得到 w 和 b 最优解的表达式:
w = ∑ i = 1 n x i y i − n x ˉ y ˉ ∑ i = 0 n x i 2 − n x ˉ 2 w = \frac{ \sum_{i=1}^{n} x_iy_i-n\bar{x} \bar{y}}{ \sum_{i=0}^{n} x_i^2-n\bar{x}^2} w=∑i=0nxi2−nxˉ2∑i=1nxiyi−nxˉyˉ
b = y ‾ − w x ‾ = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 b = \overline{y}-w\overline{x}=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}(x_i-\bar{x})^2} b=y−wx=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)(yi−yˉ)
3.3.2 梯度下降法(Gradient Descent)
- 梯度下降是一种迭代方法
- 一个用来求函数最小值的方法
- 是一种基于搜索的最优化方法
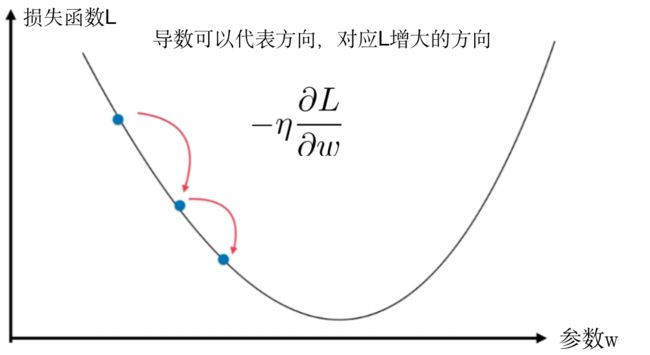
在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值
梯度下降法的流程
- 初始化参数 w , b w,b w,b
- 计算参数的梯度,并更新参数的值
w i ← w i − η ∂ L ∂ w w_i\leftarrow w_i - \eta\frac{\partial L}{\partial w} wi←wi−η∂w∂L - 根据第二步反复迭代,找到损失函数最小时的参数值
- 迭代次数
- 梯度小于我们事先设定的一个正极小值
- 前后 2 次迭代变量之间的差异小于一个正极小值
梯度下降法的公式:
w j = w j − η ∂ L ∂ w j w_j = w_j - \eta \frac{\partial L}{\partial w_j} wj=wj−η∂wj∂L
梯度下降法的公式:
w j = w j − η ∂ L ∂ w j w_j = w_j - \eta \frac{\partial L}{\partial w_j} wj=wj−η∂wj∂L

3.4 如何评价模型的好坏
误差:
E = 1 n ∑ i = 1 n e n = 1 n ∑ i = 1 n [ y ^ i − ( b + w x i ) ] 2 E =\frac{1}{n} \sum_{i=1}^{n}e^n= \frac{1}{n} \sum_{i=1}^{n}[\hat{y}^i-(b+wx^i)]^2 E=n1i=1∑nen=n1i=1∑n[y^i−(b+wxi)]2
MSE:误差平方和,越趋近于0表示模型越拟合训练数据
M S E = 1 n ∑ i = 1 n ( y t r u e i − y p r e i ) 2 MSE = \frac{1}{n}\sum_{i=1}^{n}(y_{true}^i-y_{pre}^i)^2 MSE=n1i=1∑n(ytruei−yprei)2
RMSE:MSE的平方根,作用同MSE
MAE:平均绝对误差是绝对误差的平均值,衡量预测值和真实值之间的误差,公式如下:
M A E = 1 n ∑ i = 1 n ∣ y t r u e i − y p r e i ∣ MAE = \frac{1}{n}\sum_{i=1}^n|{y}^i_{true}-y_{pre}^{i}| MAE=n1i=1∑n∣ytruei−yprei∣
TSS:总平方和 TSS(Total Sum of Squares),表示样本之间的差异情况
T S S = ∑ i = 1 n ( y t r u e i − y m e a n ) 2 TSS=\sum_{i=1}^{n}(y_{true}^i - y_{mean})^2 TSS=i=1∑n(ytruei−ymean)2
y m e a n = 1 n ∑ i = 1 n y t r u e i y_{mean} = \frac{1}{n}\sum_{i=1}^{n}y_{true}^i ymean=n1i=1∑nytruei
RSS:残差平方和RSS(Residual Sum of Squares),表示预测值和样本值之间的差异情况
R S S = ∑ i = 1 n ( y t r u e i − y p r e i ) 2 RSS = \sum_{i=1}^{n}(y_{true}^i-y_{pre}^i)^2 RSS=i=1∑n(ytruei−yprei)2
R 2 R^2 R2:称为决定系数,值越大表示模型越拟合训练数据;最优解是1,表示目标变量的预测值和实际值之间相关程度平方的百分比,公式如下:
R 2 = 1 − R S S T S S = 1 − ∑ i = 1 n ( y t r u e i − y p r e i ) 2 ∑ i = 1 n ( y t r u e i − y m e a n ) 2 R^2 = 1-\frac{RSS}{TSS}=1-\frac{\sum_{i=1}^{n}(y_{true}^i-y_{pre}^i)^2}{\sum_{i=1}^{n}(y_{true}^i - y_{mean})^2} R2=1−TSSRSS=1−∑i=1n(ytruei−ymean)2∑i=1n(ytruei−yprei)2
- RSS 表示使用我们的模型预测产生的误差;
- TSS 表示使用样本平均值进行预测产生的误差。
3.5 欠拟合与过拟合
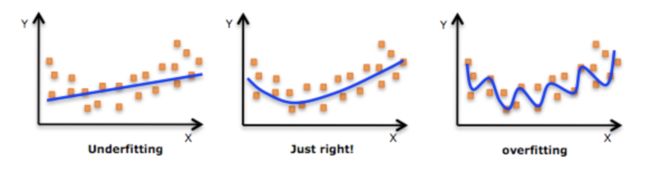
| 欠拟合 | 刚刚好 | 过拟合 |
|---|---|---|
| 模型过度简单 | 模型过度复杂 | |
| 模型无法捕获输入特征 (通常称为 X) 与目标值 (通常称为 Y) 之间的关系 | 模型可以很好的表达训练数据与测试数据的输入输出之间的关系 | 能够很好的表达训练数据上输入输出之间的关系,但是无法很好的表达测试数据上输入与输出之间的关系 |
| 模型在训练数据上表现比较差 | 模型在测试数据上表现还可以,在训练数据上表现还可以 | 模型在测试数据上表现比较差,在训练数据上表现非常好 |
4.线性回归实战
4.1 sklearn介绍
- Python 语言的机器学习工具
Scikit-learn包括大量常用的机器学习算法Scikit-learn文档完善,容易上手
4.2 sklearn 数据集
sklearn.datasets.load_*()- 获取小规模数据集,数据包含在
datasets里
- 获取小规模数据集,数据包含在
sklearn.datasets.fetch_*(data_home=None)- 获取大规模数据集,需要从网络上下载,函数的第一个参数是
data_home,表示数据集下载的目录,默认是/scikit_learn_data/
- 获取大规模数据集,需要从网络上下载,函数的第一个参数是
sklearn 常见的数据集如下:
| 数据集名称 | 调用方式 | 适用算法 | 数据规模 | |
|---|---|---|---|---|
| 小数据集 | 波士顿房价 | load_boston() | 回归 | 506*13 |
| 小数据集 | 鸢尾花数据集 | load_iris() | 分类 | 150*4 |
| 小数据集 | 糖尿病数据集 | load_diabetes() | 回归 | 442*10 |
| 大数据集 | 手写数字数据集 | load_digits() | 分类 | 5620*64 |
| 大数据集 | Olivetti脸部图像数据集 | fetch_olivetti_facecs | 降维 | 400*64*64 |
| 大数据集 | 新闻分类数据集 | fetch_20newsgroups() | 分类 | - |
| 大数据集 | 带标签的人脸数据集 | fetch_lfw_people() | 分类、降维 | - |
| 大数据集 | 路透社新闻语料数据集 | fetch_rcv1() | 分类 | 804414*47236 |
- 获取数据信息
from sklearn.datasets import load_boston
# 数据集网址:https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_boston.html
boston = load_boston()
print(boston.keys())
print("数据特征名称",boston.feature_names)
print("数据特征:",boston.data[0])
print("数据标签:",boston.target[:10])
print("数据类型:",type(boston.data), type(boston.target))
print("数据维数:",boston.data.shape)
dict_keys(['feature_names', 'data', 'DESCR', 'target', 'filename'])
数据特征名称 ['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
数据特征: [6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00]
数据标签: [24. 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9]
数据类型:
数据维数: (506, 13)
| 序号 | 特征名称 | 特征含义 |
|---|---|---|
| 1 | CRIM | 城市人均犯罪率 |
| 2 | ZN | 住宅用地所占比例 |
| 3 | INDUS | 城市中非商业用地所占尺寸 |
| 4 | CHAS | 查尔斯河虚拟变量 |
| 5 | NOX | 环保指数 |
| 6 | RM | 每栋住宅的房间数 |
| 7 | AGE | 1940年以前建成的自建单位比例 |
| 8 | DIS | 距离5个波士顿就业中心的加权距离 |
| 9 | RAD | 距离高速公路的便利指数 |
| 10 | TAX | 每一万元的不动产税率 |
| 11 | PTRATIO | 城市中教师学生比例 |
| 12 | B | 城市中黑人比例 |
| 13 | LSTAT | 城市中有多少百分比的房东属于低收入阶层 |
import pandas as pd
data_pd = pd.DataFrame(boston.data,columns=boston.feature_names)
data_pd['price'] = boston.target
data_pd.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
# 查看数据类型
data_pd.info()
RangeIndex: 506 entries, 0 to 505
Data columns (total 14 columns):
CRIM 506 non-null float64
ZN 506 non-null float64
INDUS 506 non-null float64
CHAS 506 non-null float64
NOX 506 non-null float64
RM 506 non-null float64
AGE 506 non-null float64
DIS 506 non-null float64
RAD 506 non-null float64
TAX 506 non-null float64
PTRATIO 506 non-null float64
B 506 non-null float64
LSTAT 506 non-null float64
price 506 non-null float64
dtypes: float64(14)
memory usage: 55.4 KB
# 查看数据类型
data_pd.get_dtype_counts()
float64 14
dtype: int64
# 查看数据描述
data_pd.describe()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 | 506.000000 |
| mean | 3.613524 | 11.363636 | 11.136779 | 0.069170 | 0.554695 | 6.284634 | 68.574901 | 3.795043 | 9.549407 | 408.237154 | 18.455534 | 356.674032 | 12.653063 | 22.532806 |
| std | 8.601545 | 23.322453 | 6.860353 | 0.253994 | 0.115878 | 0.702617 | 28.148861 | 2.105710 | 8.707259 | 168.537116 | 2.164946 | 91.294864 | 7.141062 | 9.197104 |
| min | 0.006320 | 0.000000 | 0.460000 | 0.000000 | 0.385000 | 3.561000 | 2.900000 | 1.129600 | 1.000000 | 187.000000 | 12.600000 | 0.320000 | 1.730000 | 5.000000 |
| 25% | 0.082045 | 0.000000 | 5.190000 | 0.000000 | 0.449000 | 5.885500 | 45.025000 | 2.100175 | 4.000000 | 279.000000 | 17.400000 | 375.377500 | 6.950000 | 17.025000 |
| 50% | 0.256510 | 0.000000 | 9.690000 | 0.000000 | 0.538000 | 6.208500 | 77.500000 | 3.207450 | 5.000000 | 330.000000 | 19.050000 | 391.440000 | 11.360000 | 21.200000 |
| 75% | 3.677083 | 12.500000 | 18.100000 | 0.000000 | 0.624000 | 6.623500 | 94.075000 | 5.188425 | 24.000000 | 666.000000 | 20.200000 | 396.225000 | 16.955000 | 25.000000 |
| max | 88.976200 | 100.000000 | 27.740000 | 1.000000 | 0.871000 | 8.780000 | 100.000000 | 12.126500 | 24.000000 | 711.000000 | 22.000000 | 396.900000 | 37.970000 | 50.000000 |
一列数据全是“number”
count:一列的元素个数;
mean:一列数据的平均值;
std:一列数据的均方差;(方差的算术平方根,反映一个数据集的离散程度:越大,数据间的差异越大,数据集中数据的离散程度越高;越小,数据间的大小差异越小,数据集中的数据离散程度越低)
min:一列数据中的最小值;
max:一列数中的最大值;
25%:一列数据中,前 25% 的数据的平均值;
50%:一列数据中,前 50% 的数据的平均值;
75%:一列数据中,前 75% 的数据的平均值;
# 计算每一个特征之间的相关系数
corr = data_pd.corr()
corr
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CRIM | 1.000000 | -0.200469 | 0.406583 | -0.055892 | 0.420972 | -0.219247 | 0.352734 | -0.379670 | 0.625505 | 0.582764 | 0.289946 | -0.385064 | 0.455621 | -0.388305 |
| ZN | -0.200469 | 1.000000 | -0.533828 | -0.042697 | -0.516604 | 0.311991 | -0.569537 | 0.664408 | -0.311948 | -0.314563 | -0.391679 | 0.175520 | -0.412995 | 0.360445 |
| INDUS | 0.406583 | -0.533828 | 1.000000 | 0.062938 | 0.763651 | -0.391676 | 0.644779 | -0.708027 | 0.595129 | 0.720760 | 0.383248 | -0.356977 | 0.603800 | -0.483725 |
| CHAS | -0.055892 | -0.042697 | 0.062938 | 1.000000 | 0.091203 | 0.091251 | 0.086518 | -0.099176 | -0.007368 | -0.035587 | -0.121515 | 0.048788 | -0.053929 | 0.175260 |
| NOX | 0.420972 | -0.516604 | 0.763651 | 0.091203 | 1.000000 | -0.302188 | 0.731470 | -0.769230 | 0.611441 | 0.668023 | 0.188933 | -0.380051 | 0.590879 | -0.427321 |
| RM | -0.219247 | 0.311991 | -0.391676 | 0.091251 | -0.302188 | 1.000000 | -0.240265 | 0.205246 | -0.209847 | -0.292048 | -0.355501 | 0.128069 | -0.613808 | 0.695360 |
| AGE | 0.352734 | -0.569537 | 0.644779 | 0.086518 | 0.731470 | -0.240265 | 1.000000 | -0.747881 | 0.456022 | 0.506456 | 0.261515 | -0.273534 | 0.602339 | -0.376955 |
| DIS | -0.379670 | 0.664408 | -0.708027 | -0.099176 | -0.769230 | 0.205246 | -0.747881 | 1.000000 | -0.494588 | -0.534432 | -0.232471 | 0.291512 | -0.496996 | 0.249929 |
| RAD | 0.625505 | -0.311948 | 0.595129 | -0.007368 | 0.611441 | -0.209847 | 0.456022 | -0.494588 | 1.000000 | 0.910228 | 0.464741 | -0.444413 | 0.488676 | -0.381626 |
| TAX | 0.582764 | -0.314563 | 0.720760 | -0.035587 | 0.668023 | -0.292048 | 0.506456 | -0.534432 | 0.910228 | 1.000000 | 0.460853 | -0.441808 | 0.543993 | -0.468536 |
| PTRATIO | 0.289946 | -0.391679 | 0.383248 | -0.121515 | 0.188933 | -0.355501 | 0.261515 | -0.232471 | 0.464741 | 0.460853 | 1.000000 | -0.177383 | 0.374044 | -0.507787 |
| B | -0.385064 | 0.175520 | -0.356977 | 0.048788 | -0.380051 | 0.128069 | -0.273534 | 0.291512 | -0.444413 | -0.441808 | -0.177383 | 1.000000 | -0.366087 | 0.333461 |
| LSTAT | 0.455621 | -0.412995 | 0.603800 | -0.053929 | 0.590879 | -0.613808 | 0.602339 | -0.496996 | 0.488676 | 0.543993 | 0.374044 | -0.366087 | 1.000000 | -0.737663 |
| price | -0.388305 | 0.360445 | -0.483725 | 0.175260 | -0.427321 | 0.695360 | -0.376955 | 0.249929 | -0.381626 | -0.468536 | -0.507787 | 0.333461 | -0.737663 | 1.000000 |
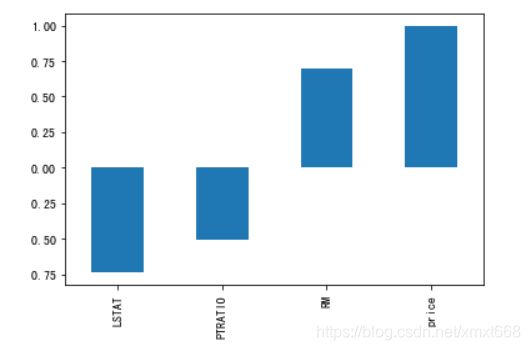
# 将相关系数绝对值大于 0.5 的特征画图显示出来
corr = corr['price']
corr[abs(corr)>0.5].sort_values().plot.bar()
绘制 LSTAT 特征与价格的散点图
import matplotlib.pyplot as plt
#设置图表大小
plt.figure(figsize=(6,4),dpi=100)
plt.scatter(data_pd['LSTAT'],data_pd['price'])
plt.ylabel('price')
plt.xlabel('LSTAT')
Text(0.5, 0, 'LSTAT')
4.3 划分数据集
把数据拆分为训练集和测试集,可以利用测试集对训练的模型进行量化地评估,衡量模型的好坏。
机器学习一般的数据集会划分为两个部分:
- 训练数据:用于训练,构建模型
- 测试数据:在模型检验时使用,用于评估模型是否有效
划分比例:
- 训练集:70% 80% 75%
- 测试集:30% 20% 25%
sklearn.model_selection.train_test_split(x, y, test_size, random_state )
x:数据集的特征值y: 数据集的标签值test_size: 如果是浮点数,表示测试集样本占比;如果是整数,表示测试集样本的数量。random_state: 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。return训练集的特征值x_train测试集的特征值x_test训练集的目标值y_train测试集的目标值y_test。
from sklearn.model_selection import train_test_split
import numpy as np
# 制作训练集和测试集的数据
y = np.array(data_pd['price'])
# data_pd=data_pd.drop(['price'],axis=1)
X = np.array(data_pd[['LSTAT']])
# 对数据集进行切分
# 训练集的特征值x_train 测试集的特征值x_test 训练集的目标值y_train 测试集的目标值y_test
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.2, random_state=22)
print("x_train:", X_train.shape)
print("y_train:", y_train.shape)
print("x_test:", X_test.shape)
print("y_test:", y_test.shape)
x_train: (404, 1)
y_train: (404,)
x_test: (102, 1)
y_test: (102,)
4.4 训练模型
4.4.1 LinearRegression 接口介绍
- 调用方法
from sklearn.linear_model import LinearRegression
lr = sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)
- 参数详解
fit_intercept:默认True,是否计算模型的截距,为 False 时,则数据中心化处理
normalize:默认 False,是否中心化,或者使用 sklearn.preprocessing.StandardScaler()
copy_X:默认 True,这个一般都采用默认值。
n_jobs:默认为 1,表示使用 CPU 的个数。当 -1 时,代表使用全部 CPU
- 获取结果
coef_:训练后的输入端模型系数,如果特征个数有两个,即 x 值有两列。那么是一个2维的数组
intercept_:截距
predict(x):预测数据
score:R2 得分
4.4.2 训练模型
from sklearn.linear_model import LinearRegression
# 创建模型
LR = LinearRegression()
#训练模型
LR.fit(X_train,y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
# 模型截距 b 的值
LR.intercept_
34.471323014406394
# 模型特征系数的值
LR.coef_
array([-0.93877786])
得到的模型为:
y = 34.47 − 0.939 ∗ L S T A T y = 34.47 -0.939*LSTAT y=34.47−0.939∗LSTAT
4.5 评估模型
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
# 输出类别数据
y_pre = LR.predict(X_test)
# print("预测值:",y_pre)
# 评估误差
print("r2_score:", LR.score(X_test,y_test))
print("r2_score:", r2_score(y_test,y_pre))
print("MSE:", mean_squared_error(y_test,y_pre))
print("RMSE:", np.sqrt(mean_squared_error(y_test,y_pre)))
print("MAE:", sum(abs(y_test-y_pre))/len(y_test))
r2_score: 0.5149044976402835
r2_score: 0.5149044976402835
MSE: 43.012248817534875
RMSE: 6.558372421381304
MAE: 5.097310907109813
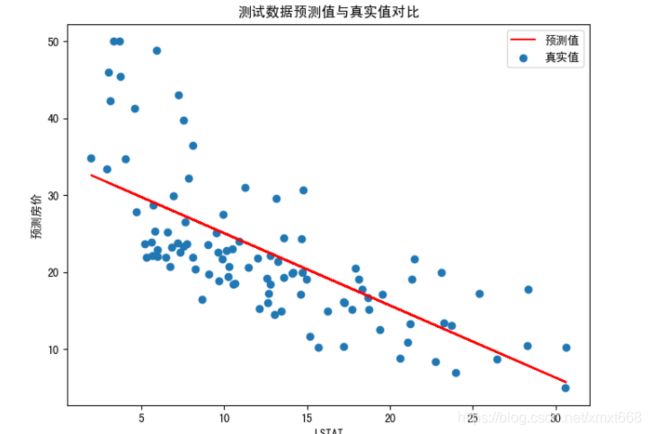
4.6 绘制结果
import matplotlib.pyplot as plt
#设置图表大小
plt.figure(figsize=(8,6),dpi=100)
#绘制预测值
plt.scatter(X_test,y_test,label="真实值")
y = LR.coef_[0]*X_test + LR.intercept_
plt.plot(X_test,y,'r',label='预测值')
plt.title("测试数据预测值与真实值对比")
plt.xlabel("LSTAT")
plt.ylabel("预测房价")
plt.legend()