python数据结构(一):数据结构与算法概述
文章目录
- 一,数据结构概述
-
- (一)什么是数据结构
- (二)数据的逻辑结构
-
- 1,集合:
- 2,线性结构
- 3,树形结构
- 4,图状结构
- (三)数据的存储结构
-
- 1,顺序存储结构
- 2,链式存储结构
- 3,索引存储结构
- 4,哈希存储结构
- 二,数据类型概述
-
- (一)python基本数据类型
- (二)抽象数据类型
- 三,算法概述
-
- (一)什么是算法
-
- 1,算法的5个重要特性
- 2,算法的5个衡量标准
- (二)算法的时间复杂度
- (三)算法的空间复杂度
- 例子:兔子的繁殖问题
-
- 使用递归:
- 使用数组:
- 使用迭代:
一,数据结构概述
(一)什么是数据结构
数据是指所有能够输入到计算机中存储并被计算机程序处理的符号的集合。
- 比如数据库中保存的学生信息。
数据元素是数据的基本单位。
- 如果以学号、 性别和姓名来标识某个学生, 那么由学号、 性别和姓名组成的学生记录将构成一个数据元素。
数据项是构成数据元素的不可分割的最小单位。
- 比如学生记录中的学号、 性别或姓名,每一项就是一个数据项。
数据对象是性质相同的数据元素的集合, 是数据的一个子集。
- 比如学生记录中的学号数据。
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。这些数据间的关联关系就是结构,数据结构通常包括数据的逻辑结构和存储结构两个层次。
(二)数据的逻辑结构
数据的逻辑结构是从数据元素的逻辑关系上抽象描述数据,可以被看作是从具体问题中抽象出来的数学模型。
根据数据元素之间的不同关系特性, 通常可将数据逻辑结构分为线性结构、集合、树形结构和图状结构。
- 后三种总称为非线性结构。
1,集合:
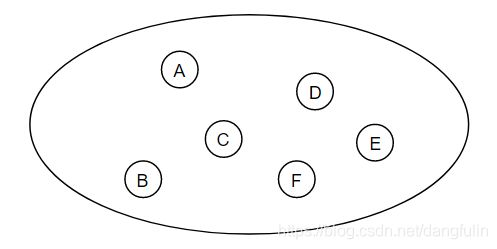
该结构中的数据元素除了属于同一集合以外, 两两之间并无其他关系。
2,线性结构
该结构中的数据元素之间存在一对多的逻辑关系。
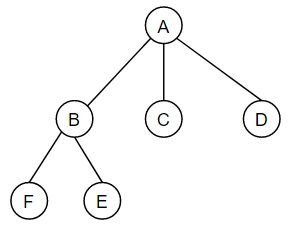
3,树形结构
该结构中的数据元素之间存在一对多的逻辑关系。
4,图状结构
该结构中的数据元素之间存在多对多的逻辑关系。
(三)数据的存储结构
数据的存储结构(又称物理结构)是指数据在计算机中的表示方法, 是数据的逻辑结构在计算机中的存储实现, 因此在存储时应包含数据元素本身及数据元素之间的关系。
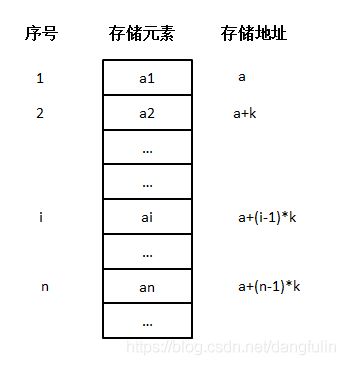
1,顺序存储结构
顺序存储结构采用一组物理上连续的存储单元来依次存放所有的数据元素。因为逻辑上相邻地两个数据元素的存储地址也相邻,所以它们的关系可以由存储单元地址间的关系来间接表示。
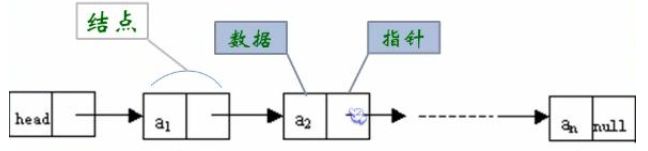
2,链式存储结构
链式存储结构用一个结点(存储这些结点的空间不一定连续)来存储一个数据元素,用附加到结点的指针来表示数据元素之间的关系。
3,索引存储结构
索引存储结构在存储所有数据元素之后,还需要建立附加的索引表来标识唯一的数据元素。
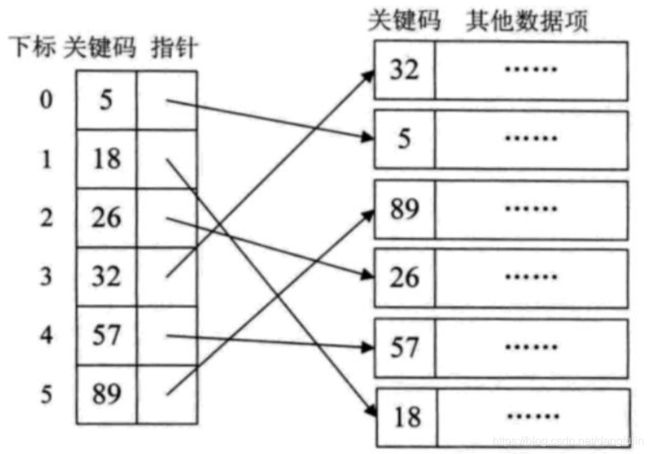
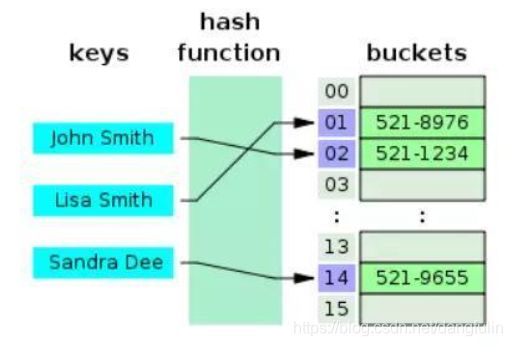
4,哈希存储结构
哈希(或散列) 存储结构根据结点的关键字来使用事先设计好的哈希(或散列) 函数计算出数据元素结点的存储地址。
二,数据类型概述
(一)python基本数据类型
数据类型是指一组值的集合及定义在这组值上的一组操作的总称。
由于python是一种强类型、动态类型的语言,其变量不需要声明,但变量在使用前必须被赋值后才会被创建和使用, 创建后变量将有具体的数据类型。
python中常用的一些内置的数据类型:数字(Number)数据类型、字符串(String )数据类型、列表(List)数据类型、元组(Tuple ) 数据类型、集合(Set)数据类型、字典(Dict)数据类型.
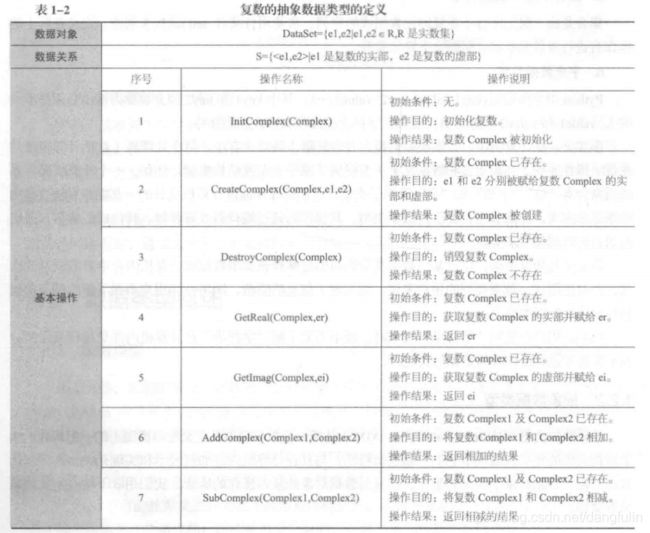
(二)抽象数据类型
抽象数据类型(Abstract Data Type, ADT)是指一个数学模型及定义在该模型上的一组操作。 具体包括数据对象、 数据对象上关系的集合, 以及对数据对象的基本操作的集合。
ADT结构表示如下:

其中基本操作表示如下:

一个示例:
特别说明,尽管我们使用的CPython版本的python提供了许多内置的数据类型,比如 List数据类型,其本身自带了 insert 方法,如果查看过其底层的C语言代码就会发现,实现的过程有相当多的细节,比如自动的内存处理操作,正是这些细节保证了内置数据类型的操作的灵活性。这是我们使用这些python内置的数据类型进行数据结构与算法实现的基础。
但是,在我们将介绍的数据结构实现中,内置数据类型的操作可能满足不了我们的需要,比如还是List的insert,默认会将超出最后位置的元素统一插入到整个序列的最后,而实际上我们希望的是它能够进行报错处理,所以我们将通过python中的委托机制对内置的数据类型进行扩展,从而实现定制化的数据结构。
正是由于对python内置数据类型依赖程度的不同,将导致你看到各种版本的python数据结构的实现,比如对顺序表的部分实现:
C++语言实现:
/*定义顺序表*/
# define MAXSIZE 5
typedef struct {
int data[MAXSIZE];
int length;
}SeqList;
/*插入操作*/
int Insert(SeqList &L, int p, int x)
{
if (L.length > MAXSIZE)
{
printf("顺序表已满!");
return 0;
}
if (p<0 || p>L.length)
{
printf("插入位置错误!");
return 0;
}
for (int i = L.length; i >= p; --i)
L.data[i+1] = L.data[i];
L.data[i] = x;
L.length++;
return 1;
}
第一种,尽量严格实现传统数据结构教程中的数据结构的定义:
class SeqList(object):
def __init__(self, maxsize=8):
self.maxsize = maxsize # 顺序表的最大长度
self.num = 0
self.date = [None] * self.maxsize
# 不考虑扩展顺序表空间
def is_full(self):
return self.num is self.maxsize
def append(self, value):
if self.is_full():
print("list is full")
return
else:
self.date[self.num] = value
self.num += 1
def insert(self, key, value):
if key < 0:
raise IndexError
# 当key大于元素个数时,默认尾部插入
if key >= self.num:
self.append(value)
else:
for i in range(self.num, key, -1):
self.date[i] = self.date[i - 1]
self.date[key] = value
self.num += 1
第二种,结合python特点实现数据结构:
class SequenceList(object):
"""
类名:SequenceList
功能:定义顺序表
"""
def __init__(self):
"""1,初始化一个空顺序表。
:param:无。
:return:无。
"""
self.SeqList = []
def InsertElement(self, element, position):
"""2,在指定位置插入元素
:param: 待插入的元素值element,待插入的位置position。
:return: 插入元素成功,返回True。
"""
if position not in range(1, len(self.SeqList) + 2):
print("位置不合法!")
return False
else:
print("正在插入元素......")
self.SeqList.insert(int(position) - 1, element)
print("插入元素后,顺序表为:", self.SeqList)
return True
我们将选择第二种方法的思路,因为第一种方法的思路就是使用高级的python模仿C++甚至更低级的C对传统数据结构进行实现,这很大程度上抛弃了python简洁灵活的特点,既然是数据结构的python实现,那么后面将会在满足数据结构逻辑结构的基础上充分利用python提供的优势进行扩展。
三,算法概述
(一)什么是算法
举个例子:计算 -1,1,-1,1,-1,…,(-1)n 之和。
最”笨“的算法:
def Sum(n):
sum = 0
n = int(n)
for i in range(1, n+1):
sum = sum + (-1)**i
return sum
if __name__ == '__main__':
n = input("输入正整数n:")
print(Sum(n))
但更”好“的方法:
def Sum(n):
n = int(n)
if (n % 2) == 0:
return 0
else:
return -1
if __name__ == '__main__':
n = input("输入正整数n:")
print(Sum(n))
虽然在思路上有区别,但是它们都是算法。
算法是对待特定问题求解步骤的一种描述, 它是指令的有限序列。
- 算法和程序是不同的, 程序是指使用某种计算机语言对一个算法的具体实现, 即程序描述了具体怎么做, 而算法侧重于描述解决问题的方法。
1,算法的5个重要特性
- 有穷性: 一个算法对于任何合法的输入必须在执行有穷步之后结束, 且每一步都可在有穷的时间内完成。
- 确定性: 算法中每一条指令都必须具有确切的含义, 不能有二义性, 并且在任何条件下,算法的任意一条执行路径都是惟一的, 即对于相同的输入所得的输出相同。
- 可行性: 一个算法是可行的, 是指算法中描述的操作都可以通过基本运算执行有限次操作来实现。
- 输入: 一个算法有零个或多个输入, 这些输入取自于某个特定对象的集合。
- 输出: 一个算法有零个或多个输出, 这些输出是同输入有着某些特定关系的量
2,算法的5个衡量标准
- 正确性: 要求算法能够正确地执行, 并满足预先设定的功能和性能要求。
- 可读性: 一个算法的可读性好才便于人们理解, 人们才有可能对程序进行调试, 并从中找出错误。
- 健壮性: 当输入的数据不合法或运行环境改变时, 算法能恰当地做出反应或进行处理。
- 时间复杂度: 对一个算法执行时间效率的度量。
- 空间复杂度: 对一个算法在执行过程中所占用的存储空间的度量。
(二)算法的时间复杂度
算法的执行时间是通过依据该算法编写的程序在计算机上执行时所需要的时间来计算的,具体可以参考下面两篇:
算法时间复杂度分析,算法—时间复杂度,一场面试,带你彻底掌握递归算法的时间复杂度
(三)算法的空间复杂度
算法的空间复杂度一般也认为是问题规模 n 的函数。在对算法的空间复杂度进行研究时, 只分析临时变量所占用的存储空间。
第16话:算法的空间复杂度,算法分析中的空间复杂度,程序员算法面试中,递归算法的空间复杂度你知道怎么求么?
例子:兔子的繁殖问题
一对兔子,从出生后第2个月起每个月都生一对兔子。小兔子长到第2个月后每个月又生一对兔子。假如兔子都不死,请问第n个月后有多少对兔子?
分析一下:
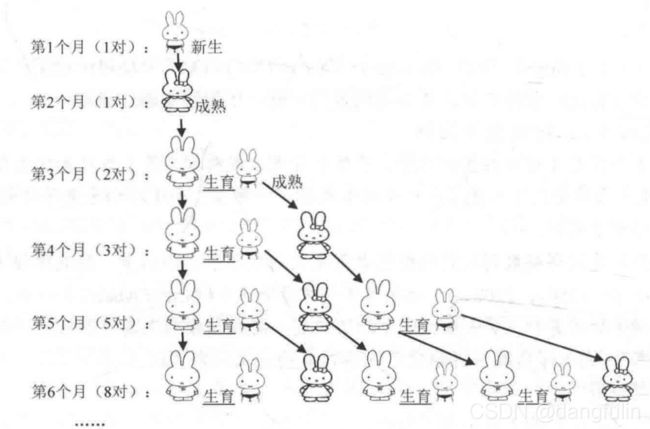
这些对数1, 1, 2, 3, 5, 8,… ,构成斐波那契数列,其算法的递归式表达式为:
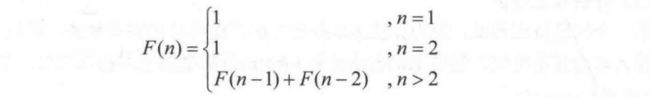
使用递归:
既然有现成的数学表达式,那么程序就很简单了:
def Sum(n):
n = int(n)
if n < 1:
return -1
if (n == 1) or (n == 2):
return 1
return Sum(n - 1) + Sum(n - 2)
if __name__ == '__main__':
n = input("输入正整数n:")
print(Sum(n))
运行程序进行验证是没有问题的,但随着问题规模越来越大,所需的计算时间增长非常快:
import time
def Sum(n):
n = int(n)
if n < 1:
return -1
if (n == 1) or (n == 2):
return 1
return Sum(n - 1) + Sum(n - 2)
if __name__ == '__main__':
n = input("输入正整数n:")
start = time.perf_counter()
print(Sum(n))
end = time.perf_counter()
print("total time: ", end - start)
环境: win10专业版 酷睿i7-9750h 32GBRAM
输入正整数n:1
1
total time: 4.710000000018866e-05
输入正整数n:10
55
total time: 4.789999999976757e-05
输入正整数n:20
6765
total time: 0.002984600000000004
输入正整数n:30
832040
total time: 0.31894920000000004
输入正整数n:40
102334155
total time: 40.9772339
因为根据斐波拉契通项求得的这个算法时间复杂度是指数阶的,所以这个算法的时间复杂度是相当大的!而且,这个递归算法的空间复杂度是O(n)。
尽管这个算法实现起来很简单,但由于多次递归会导致时间以指数形式上升,所以可以通过减少递归次数来优化算法。
使用数组:
既然斐波那契数列中的每一项是前两项之和,如果记录前两项的值,则只需要一次加法运算就可以得到当前项,这就能避免使用递归:
import time
def Sum(n):
n = int(n)
if n < 1:
return
elif (n == 1) or (n == 2):
return 1
else:
temp = [0] * n
temp[0] = 1
temp[1] = 1
for i in range(2, n):
temp[i] = temp[i - 1] + temp[i - 2]
return temp[-1]
if __name__ == '__main__':
n = input("输入正整数n:")
start = time.perf_counter()
print(Sum(n))
end = time.perf_counter()
print("total time: ", end - start)
环境: win10专业版 酷睿i7-9750h 32GBRAM
输入正整数n:1
1
total time: 2.7199999999893976e-05
输入正整数n:10
55
total time: 3.2000000000032e-05
输入正整数n:20
6765
total time: 3.399999999986747e-05
输入正整数n:30
832040
total time: 3.509999999984359e-05
输入正整数n:40
102334155
total time: 3.6600000000053257e-05
这个算法的时间复杂度为 O(n) ,直接从指数阶降到了多项式阶,但由于使用了 一个长度为 n 的辅助数组记录中间结果,所以时间复杂度为 O(n)。
实际上这个数组仅仅是起到一个记录中间数据的作用,这是能够进行优化的。
使用迭代:
在迭代中使用辗转相加法取代数组:
import time
def Sum(n):
n = int(n)
if n < 1:
return
elif (n == 1) or (n == 2):
return 1
else:
temp1 = 1
temp2 = 1
for i in range(2, n):
temp2 = temp2 + temp1 # 辗转相加法
temp1 = temp2 - temp1
return temp2
if __name__ == '__main__':
n = input("输入正整数n:")
start = time.perf_counter()
print(Sum(n))
end = time.perf_counter()
print("total time: ", end - start)
环境: win10专业版 酷睿i7-9750h 32GBRAM
输入正整数n:1
1
total time: 2.4400000000035504e-05
输入正整数n:10
55
total time: 3.019999999986922e-05
输入正整数n:20
6765
total time: 3.0499999999822336e-05
输入正整数n:30
832040
total time: 3.229999999998512e-05
输入正整数n:40
102334155
total time: 3.3200000000288554e-05
这个算法的时间复杂度为 O(n) 没变,但空间复杂度为 O(1)!