Python编写程序求解一元二次方程，打印九九乘法表，判断三条边是否可以构成三角形，并求三角形面积

目录

求解一元二次方程题目总体要求如下：

打印九九乘法表题目总体要求如下：

判断三条边是否可以构成三角形题目要求如下：

---

求解一元二次方程题目总体要求如下：

编写程序，输入一元二次方程的三个系数a、b、c，求方程ax^2+bx+c=0的解。

注：此方程的解有以下几种情况：

1.a=0 and b=0，无解。

2.a=0 and b!=0，有一个实根，x=c/b

3.b^2-4ac=0，有两个相等实根：x1=x2=-b/(2a)

4.b^2-4ac>0，有两个不等的实根，x=

5.b^2-4ac<0，有两个共轭复根，x=

注：在共轭复根那里，我们老师要求的是分别计算出实部和虚部再手动加上i，我使用的是jupyter编译器，如果直接计算出复数的话好像是用j表示的。

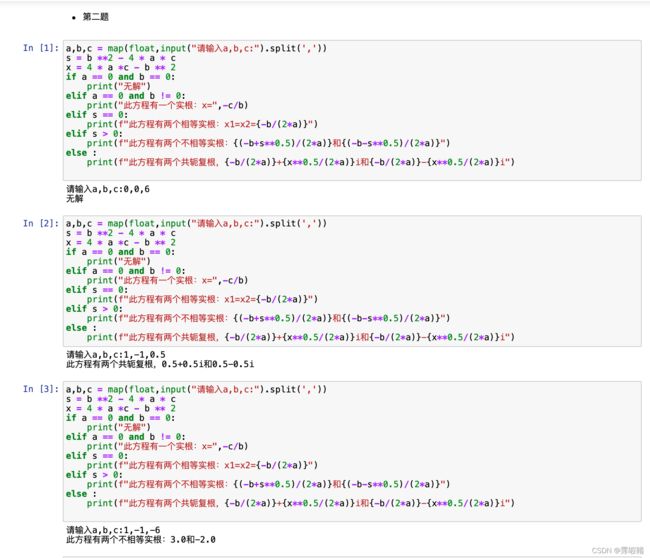
如下是代码段：

a,b,c = map(float,input("请输入a,b,c:").split(','))
s = b **2 - 4 * a * c
x = 4 * a *c - b ** 2
if a == 0 and b == 0:
    print("无解")
elif a == 0 and b != 0:
    print("此方程有一个实根：x=",-c/b)
elif s == 0:
    print(f"此方程有两个相等实根：x1=x2={-b/(2*a)}")
elif s > 0:
    print(f"此方程有两个不相等实根：{(-b+s**0.5)/(2*a)}和{(-b-s**0.5)/(2*a)}")
else :
    print(f"此方程有两个共轭复根，{-b/(2*a)}+{x**0.5/(2*a)}i和{-b/(2*a)}-{x**0.5/(2*a)}i")
    

部分运行结果如图：

打印九九乘法表题目总体要求如下：

编写程序，打印九九乘法表，要求输出九九乘法表的各种显示效果（上三角、下三角、矩形块等方式）

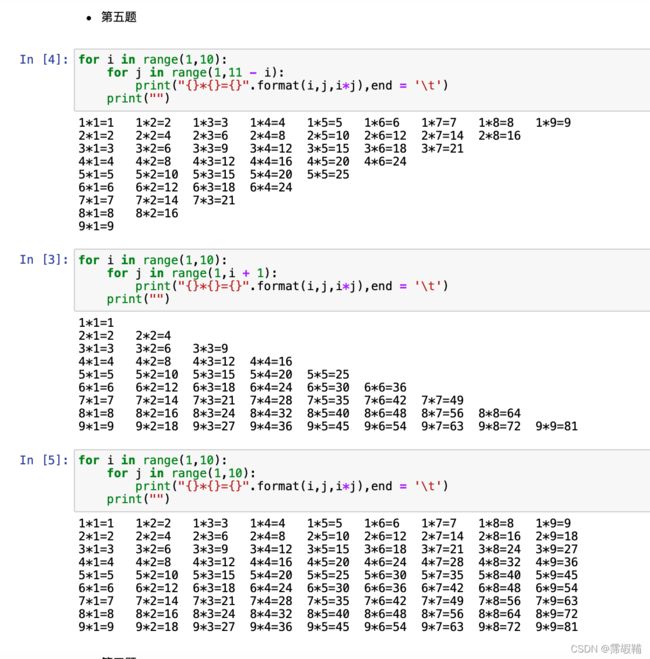
如下是代码段：

for i in range(1,10):
    for j in range(1,11-i):
        print("{}*{}={}".format(I,j,i*j),end = '\t')
    print("")

for i in range(1,10):
    for j in range(1,i+1):
        print("{}*{}={}".format(I,j,i*j),end = '\t')
    print("")

for i in range(1,10):
    for j in range(1,10):
        print("{}*{}={}".format(I,j,i*j),end = '\t')
    print("")

部分运行结果如图：

判断三条边是否可以构成三角形题目要求如下：

编写程序，输入三角形三条边，先判断是否可以构成三角形，如果可以，则进一步求三角形的面积，否则报错：“这不是一个三角形！”。

如下是代码段：

a = float(input("请输入三角形边A："))
b = float(input("请输入三角形边B："))
c = float(input("请输入三角形边C："))
print(f"三角形三边分别为：{a},{b},{c}" )
if a < 0 or b < 0 or c < 0:
    print("边长不可能为负数")
elif a + b < c or a + c < b or b + c < a:
    print("这不是一个三角形")
else :
    s = (a + b + c)/2
    area = (s * (s - a) * (s - b) * (s - c))**0.5
    float(area)
    print(f"三角形面积为：{area}")
    

部分运行结果如图：

这是我们python作业中的几题，算不上难，就算是简单记录一下自己的学习过程吧，如果有什么问题，欢迎大家提出，我来改正！