概率图模型和马尔可夫模型

概率图模型和马尔可夫随机场

1.什么是概率图模型

绝大多是机器学习的目的就是从给定的数据中学习到数据的特点，从给定的数据中找出数据与数据之间的关系。但是对于有一些数据而言，数据与数据之间的关系无法直接并且准确地从给定数据中观察到，因为这样的数据存在着一个或者多个隐变量。这些隐变量使得属性之间的联系变得更加的复杂。所以我们需要一个模型来清晰地表示变量与变量之间关系的概率模型。我们将变量作为一个节点，将变量之间的关系用线来表示，然后把所有有关联的变量连接起来，就形成了我们所谓的概率图模型。

概率图模型根据数据点之间的相互关系，可以分成贝叶斯网(有向图模型)和马尔可夫网(无向图模型)

1.1 有向图模型

通常有向图是用概率拼接起来的。因为有向图中，变量与变量之间的依赖关系我们可以观测或者预估。若变量之间的依赖关系已知，那么整个图模型就可以使用所有的变量的联合概率分布来表示。为了更容易理解，我们假设我们有一组观测变量X={x1,x2,x3,x4}，这四个观测变量的依赖关系如下图所示:

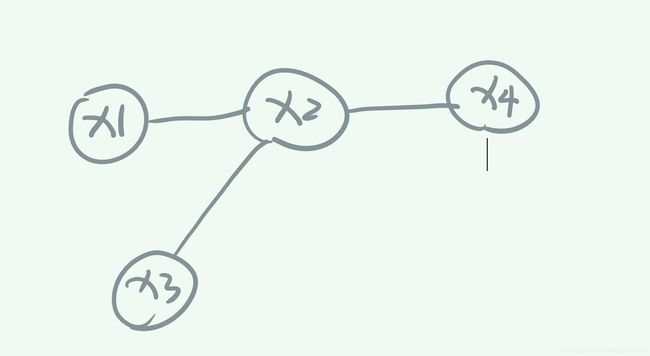
这个图的意思是，X1，X3是独立的，他们的出现不依赖于集合中的任何变量。然而，X2的出现依赖于X1和X3两个变量，X4的出现依赖于X2。
按照这样的逻辑，我们可以很轻松的写出这一个有向图模型的表达式，用联合概率分布表示为：

所以根据上面的式子，我们可以这样来解释有向图：有向图就是将一整个联合概率分布分成了一个一个独立于单个变量的条件概率分布。

A directed graphical model describes how a distribution factorizes into local conditional probability distributions.

1.2 什么是无向图模型

无向图模型数据与数据直接没有可观测或者可预估的依赖关系，且往往有着较大的数据量。比如图片中的每一个像素点之间没十分明确的依赖关系。所以这个时候我们无法直接用概率将无向图进行拼接。但是我们也想要找到无向图之间变量的依赖关系。于是，我们将一个无向图分成一个一个小块(这样的小块叫做团)，来研究每一个小块中变量的依赖程度。团中的两两元素应该相互连接。如果一个团无法在容下另外的团，那么这样的团我们称之为最大团。那团中元素的依赖程度我们怎么来求解？这里要引入一个叫做势函数的概念.势函数的作用就是用来刻画每一个团中的元素相关性的。假设我们使用C来表示一个无向图的团的集合，那么这个无向图我们可以表示成：

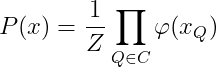
这里的Z叫做规范化因子。我们要注意的是，如果一个团不是最大团，那么他一定属于某一个最大团。如果我们以所有的团来进行建模，会出现很多不必要的重复运算。所以，C应该是所有最大团的合集。

1.3 马尔可夫模型

马尔可夫模型就是一个非常经典的有向图模型。既然是有向图的一种，那么马尔可夫模型，就一定包含有向图的基本特征。那么如何来确定一个马尔可夫模型呢？？

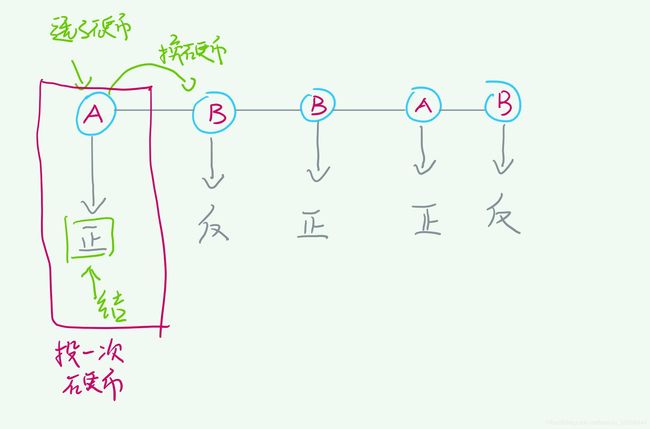
我们还是用抛硬币的例子来解释马尔可夫模型。我们假设有两枚硬币，每一次随机从两枚硬币中拿出一枚进行投掷，并记录下结果(正面还是反面)，以上步骤重复5次，意思是，我们应该随机从两枚硬币中拿5次并且记录5次结果。
在以上的情景中，什么是隐变量？隐变量是我们每一次选择的硬币是A还是B，这些无法观测。什么是观测变量? 也就是我们每一次投掷的结果，这个是可以观测到的。现在我们所能想到的变量就这些了，那我们将这些变量用上面提到的图的方式，连接起来能得到什么呢？

从上图中，蓝色圈圈表示隐变量，也就是我们随机拿的硬币，这个在马尔可夫模型中叫做状态,假如我们拿了硬币A来投，投出了正面，那么这个正面(图中用绿色框框划出来的)就是观测变量(observations)。那投完了第一次硬币之后，我们又要再一次从AB中拿一枚来投，这时候拿到的可能是硬币B，也有可能还是硬币A。再一次拿硬币这个过程在马尔可夫模型里也有专业的定义，我们可以叫它状态转移。

现在我们来定义马尔可夫模型的三个重要参数：

• 初始状态变量(Initial Probability)
  初始状态变量通常指的是第一个状态变量出现的概率。也就是第一次取硬币是取到A还是B的概率，假设用$\pi$来表示初始状态概率，y表示当前状态，初始状态变量可以表示成：

• 输出观测概率/发射概率(Emission Probability)：
  发射概率阐述的是当前状态下，输出观测变量为$x_i$的概率。
  结合硬币的例子，当我现在拿到了硬币A，出现正面或者反面的概率是多少。

• 状态转移概率：
  状态转移概率阐述了，模型之间每个状态之间相互转移的概率。
  同样的结合硬币例子来理解。就是第一次取到了硬币A来投掷了。那么下一次我取到硬币A或者硬币B的概率。

这里有一个有趣的现象， 每次一投硬币的结果只和当前选取的硬币有关，去其他的变量无关，每一次随机抽取的硬币是A还是B，只和上一次投掷的硬币有关。换句话说在任意时刻，观测变量只和状态变量有关，而且当前时刻的状态仅和上一时刻的状态有关，去其他时刻无关。这样的现象(约束)被称为‘马尔可夫链’ 。

当我们可以从数据中找出上述的三种参数，并且数据的依赖规则满足‘马尔可夫链’的约束，那么我们就可以用马尔可夫模型对这样的数据进行建模。

1.4 D-separation

在进入马尔可夫模型常见问题之前，有必要先了解什么叫做D-separation。它阐述了每个变量之间的相互依赖关系。也就是说，在给定的一个图G中，可以通过D-separation来判断属于图G中的两个子合集A和B是不是相互独立。

它有三条重要的规则：
1.A与B是 D-connected,如果AB之间没有碰撞点(collider)。换句话说，如果他们之间有碰撞点，那么他们就是相互独立的。
什么是碰撞点？举个例子，如下如所示，这里的箭头并不是代表的方向，因为我们在这里不讨论方向，箭头可以理解成变量间相互依赖关系。在下图中，碰撞点是a4。简单地理解，当箭头出现‘头对头’的情况(head to head)，那么箭头中间的那一个点就可以叫做‘碰撞点’。

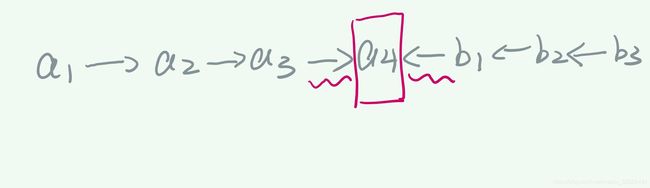
我们可以发现，在这种情况下，只要经过碰撞点，箭头的方向就发生了变化，我们理解成变量之间的依赖关系发生了变化。所以在下图中，a1与a2是相互依赖的，同理a2，a3也是。但是a1与b1是相互独立的，因为无论如何都无法避免依赖关系发生改变，也就是无法在a1和b1之间找到一条箭头方向不改变的"路径"。注意，这里的讨论前提条件是无条件,意思是只讨论两个集合的情况。

2.有条件的约束。
因为第一种约束存在着局限性，在有些情境下可能无法使用。比如没有碰撞点存在的时候。如何使得两个变量条件独立呢？我们引入一个条件合集Z，如果Z中的元素出现在了
"路径"中间，那么这条路径就可以说是被Z阻断了。可以理解成，变量之间的依赖关系被新加入的元素打断，我们可以设想如图所示的情况。

上图中，X1,X2依旧是相互依赖的，因为他们之间没有元素加入，也没有碰撞点，但是X2和X3就是相互独立的，因为依赖关系被Z1阻断。这个条件的使用也有一个前提，那就是如果存在这个碰撞点，碰撞点不可以在Z这个集合中

3.当碰撞点在条件集中
如果碰撞点出现在了条件集合中，又或者说，碰撞点的子代(descendant)在条件集合中，那么这个时候碰撞点将不会阻断任何“路径”。这里很抽象，什么意思？意味着当上述情况出现之后，原本独立的两个或多个变量变得相互依赖。如下图所示

本来应该被碰撞点a3截断的路径，因为碰撞点的子代在条件集合Z中，导致从a1到b2都相互依赖。

详细D-separation的解释可以参考D-separation without tears

1.5 马尔可夫模型的常见问题和解决方法

根据上面的描述，我们可以大致的推断出马尔可夫模型的几种常见问题。

• Inference problem(推断问题)
  我们只知道观测变量和参数，需要预测状态序列的时候。比如在硬币问题中，我们知道三个关键参数和每一次投掷的结果，来推断投掷的是A还是B。
  这种问题有两种常见的方法，一种brute-force(暴力法)和Viterbi算法。

  暴力法，显而易见，就是尝试每一个可能的状态组合取出使得联合概率最高的状态。但是通常这样的做法都是不可取的，特别是遇到数据量巨大的情况。因为如果是一个二选一的问题，那么我们就有$2^2=4$个可能的状态序列，如果有N个可能的状态，那么就有$2^N$个可能的序列，计算压力极大，时间复杂度极高。
  所以我们会使用Viterbi算法来高效的推断出最佳的状态序列。

  Viterbi算法本身是动态规划算法，动态规划的核心就是将一个大问题分成多个小问题。秉持着所有sub-problems的最优解之和就是全局最优解的思想，我们也可以将inference 问题 分成多个小块来求解。我们每一次只计算一个状态，并保证每一次取到的状态都能使当前时刻与观测变量的联合分布最大，如果每一步取到的状态变量都能使当前的联合分布最大的话，那么最后找出的状态变量序列也一定可以让联合分布最大化。

  具体怎么做：
  我们首先创建一个变量${\sigma }_i$来表示从第1个时刻开始到当前时刻，所选状态和观测变量的联合概率分布，我们在整个过程中都应该保持${\sigma }_i$ 最大化。$\sigma$可以定义成：

  

  为了可视化整个过程，下面用一个表格来表示：

  

  图中的横轴Z1-Z5表示的是5个时刻的状态，纵轴上的1-5表示的是每一个时刻可能取到的状态。因为我们知道初始状态概率，所以我们可以求出Z1时刻下能使联合概率分布最大的状态变量。在Z2时刻时，每一次计算应该是基于Z1时刻的结果，具体可以表示成：

  

计算从$Z_1$转移至$Z_2$的状态转移矩阵，再加上$Z_1$时刻的$\sigma$值，我们取出其中最大的结果作为$Z_2$的值。

然后重复上述步骤，计算每一个节时刻的状态值。使得最后联合概率分布最大的序列就是最佳的状态序列。如下图所示表示的最佳状态序列就是23154。

• 参数估计问题
  参数估计的目标一定是估计发射概率，转移概率以及初始概率这三个参数。那么参数估计本身有两种情况，complete case 和 incomplete case。所谓的complete case 就是观测变量和状态变量全部已知,那么参数估计就可以写成’$p(x|z)$’，而 incomplete case 就是没有只有观测变量已知，但是状态变量未知的情况’$p(x|?)$’。

  对于第一种情况，往往我们只需要做一些简单的统计就可以找出合适的参数了，相对比较容易处理。比如说，我们想要知道初始状态概率，只需要将每一种状态变量作为第一个状态的次数除以总共的样本数即可。发射概率和转移概率也是用类似的简单统计思想。

  通常我们需要讨论第二种情况。在状态变量未知的情况下，是无法对三个关键参数进行预估的。所以这时我们可以用到EM算法的思想来对状态变量进行预估，从而预估参数。(如果对EM算法不太熟悉，可以参考EM算法的理解和证明这篇博客。

  现在思考状态变量在马尔可夫模型中能决定什么？？他可以决定当前状态下的输出观测变量和下一时刻的状态变量。所以我们可以用这一个关系，来求出当观测变量给定时，所有状态出现的概率：

  
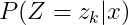
  相当于我们可以通过上述的方式来求出状态变量的expectation，将一个incomplete case 转换成了一个complete case。之后我们就可以推算三个关键参数的值，然后再使用估算出的参数的值去更新状态变量的expectation。

  我们现将在这个公式用贝叶斯公式展开：
  

  上述公式中，我将已知的观测变量合集z,拆分成了两个，一个包含了从第一个观测变量到第K个，第二包含了从第K+1个观测变量到最后一个。这么做的原因是，可以使后面的数学证明更加清晰。

  前面有讲到，有向图是将一个大的联合概率分布拆分一个一个的基于单个变量的条件概率分布。 对于上述式子而言，我们还可以将其表达成：

  
  根据D-separation的第二条性质，我们可以断定，$x_{1:k}$和$x_{k+1:n}$是相互依赖的，所以$x_{1:k}$对当前分布不造成影响，所以：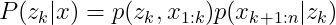

  
  上述的表达式，其实是一种新算法叫做前向-后向算法(forward-backward algorithm)。 这个算法其实是前向和反向算法的总称，在上述式子上$p(z_k,x_{1:k})$就是前向算法，$p(x_{k+1:n}|z_k)$就是反向算法。

1.6 总结

有向图和无向图之间最明显的区别就是有向图中每个变量的相互依赖关系是已知或者可观测的，所以有向图模型可以使用所有变量的联合概率分布来表示，也就是可以使用概率拼接。但是无向图中因为无法使用概率来进行拼接，我们将一个无向图分成多个最大团，来研究团中元素的依赖程度。

马尔可夫模型是一个典型的有向图模型，定义它的三个参数是，初始概率，发射概率，和状态转移概率，它收到马尔可夫链的约束。对于马尔可夫模型问题的求解方式，可以发现很不管是推断问题还是参数估计问题，都用到了动态规划算法的思想。forward算法本身也用到了动态规划算法的思想。