机器学习数据基础：线代（4）

2.5 线性独立

下面我们看看向量（向量空间的元素）可以干撒，通过闭包的特性， 我们可以找到一组向量通过他们的相加和与标量的相乘可以表示向量空间中的任意向量，就是基啦，在这之前我们介绍一下线性组合和线性独立。

线性组合：考虑一个线性空间V，和有限个向量 x1, . . . , xk ∈ V，每个V的向量可以表示为，其中λ1, . . . , λk ∈ R 就是向量x1…xk 的线性组合。零向量总是一个线性组合，毕竟总是零向量嘛，下面我们讨论代表零向量的一组特别的线性组合，即不是所有的入i 都是0。

线性独立/相关：x1, . . . , xk ∈ V，如果有一个特别的线性相关，像 λixi 的和是零向量，其中至少一个入i 不是零，这些向量 xi 就是线性相关，如果只有λ1 = . . . = λk = 0 这就是线性独立

线性独立是线代中最重要的概念，线性独立的向量所包含的向量是没有冗余的，即每个都是有用的。

一个栗子：

这个地理上的栗子，首先 紫色向量和蓝色向量是线性独立的，这俩无法相互描述，他俩合成黑色的向量，加上这个就构成了线性相关。所以可以用来指路？？？？原来要说两句话，现在只要一句话就行了，是不是很有用。。。。

备注：判断线性独立的方法

• k个向量只有相关或独立，没有别的
• 如果至少有一个零向量，他们就是线性相关。如果由两个向量相同也是相关。
• {x1, . . . , xk : xi = 0, i = 1, . . . , k}, k > 2，当前仅当他们中至少有一个是其他的向量的线性组合，那就是线性相关的。特别是如果一个向量是其他向量的倍数，即xi =入xi，那向量集合就是线性相关的
• 检查是否线性独立的一个方法是高斯消除：写下所有的向量作为矩阵A的列，然后使用高斯消除化为阶梯型（不用化成精简的形式）：

1. 枢纽列代表的向量与左侧的向量是线性独立的（书上说左侧，我感觉应该是右侧吧。。），注意再建立矩阵时向量的顺序。
2. 非枢纽列可以使用枢纽列的线性组合表示。就像这个阶梯型，我们可以看出一三行是枢纽列，第二行是非枢纽列，因为第二行是第一行的三倍。

如果所有的列都是枢纽列，那所有的列向量都是线性独立的。如果至少有一个非枢纽列，这些列就是线性相关的

一个栗子：

化成阶梯型后，每一列都是枢纽列，因此没有非平凡解， λ1 = 0, λ2 = 0, λ3 = 0 才是解。x1 x2 x3时线性独立的。

备注：考虑一个线性空间，有k 个线性独立的向量b1,bk 和m个线性组合

定义 B = [b1, . . . , bk] 为矩阵，矩阵的列b1,bk是线性独立的可以写为这种形式
然后我们想测试一下 x1 ,xm是否是线性独立，我们使用通用的方法来测试。这个就是线性无关的定义
这意味着 {x1, . . . , xm}是线性独立的，只要列向量 {λ1, . . . , λm}是线性独立。

另外，k个向量的（x1,xk）的m个向量组合，如果m>k 那些向量就线性相关

举个栗子：
考虑一个线性无关的向量b1 b2 b3 b4 和
向量x1,x4是线性无关嘛？我们构造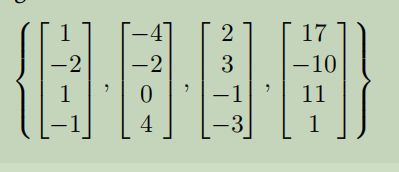 看看这列向量是否线性无关。
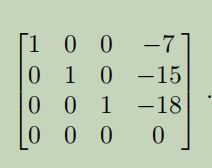可以看出 x4 = -7x1 - 15x2 -18x3。因此这四个是线性相关的，x4是x1,x3的线性组合。

2.6 基和秩

再向量空间中，我们研究了任何向量可以通过其他向量的线性组合来表示（再同一向量空间中）的特性。这些向量是特别的，下面就说道说道。。

2.6.1 生成集合和基

生成集合和生成空间（span 是不是这个意思来）：考虑一个集合空间V，和一个集合a={x1,x2,xk}属于v ，如果每个向量v可以使用x1,xk的线性组合来表示，a就叫 V 的生成集和。这个集合a中的向量所有线性组合和集合就叫a的生成空间。如果a的生成空间是向量空间V ，记V = span[A] or V = span[x1, . . . , xk]

生成集合是生成向量（子）空间向量的集合（Generating sets are sets of vectors that span vector (sub)spaces，是不是这个意思），也就是说，每个向量可以使用生成集中的向量的线性组合来表示

基：考虑一个向量空间V，和 a ⊆ v .如果生成空间V中不存在更小的集合
，那V的生成集合a 叫最小（minimal）。V的每一个线性独立的生成集合都是最小的，并叫作V的基。

V = (v , +, ·) 是向量空间，b属于v，b不是空集。下面的称述都是相等的：

• b是V的基
• b是最小生成集合
• b是V中向量的最大线性独立集合，也就是说增加任何其他向量进去就是线性相关了。
• 每个向量x 属于 V 都是b 中向量的线性组合，每个线性组合都是唯一的。
  λi , ψi ∈ R, bi ∈ B 这里λi = ψi , i = 1, . . . , k.

举个栗子：

再R^3 中，标准的基就是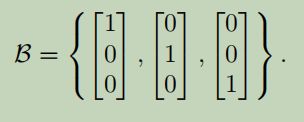（别看上面说的花里胡哨，基就是这东西）

A是线性独立，但不是生成集（也不是基）, 例如[1,0,0,0]T 就不能使用A中元素的线性组合获得。

每个向量空间都有基，之前的栗子展示了一个向量空间可以有很多基，也就是基不是唯一的。但是所有的基向量都基本拥有相同的元素。

我们只考虑有限维的向量空间V，着这个了栗子中，V的维数就是基向量的个数，记dim(V),如果U 是V的子空间 dim(U) <= dim(V ) ，如果U =V 等号成立。直观来看，向量空间的维数可以认为是再这个向量空间中独立方向的个数（二维三维坐标系嘛）。

另外：向量空间的维数不需要是向量中元素的数量。例如向量空间V=span[ [0 1]T ]是一个一维向量，尽管基向量是二维的。

另外，子空间的基 U = span[x1, . . . , xm] ⊆ Rn 可以通过以下步骤来找：

• 将生成向量写为矩阵A的列
• 化成阶梯型
• 与枢纽列对于的生成向量就是U的基

举个栗子：

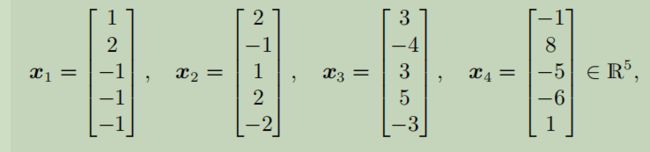
这些向量生成向量子空间 U ⊆ R5 。我们现在想知道这四个是不是U 的基。也就是检查x1,x4是否是线性独立的。因此我们需要解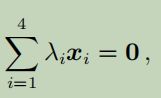这构成了矩阵形式的齐次线性方程组

枢纽列表示了那些向量是线性独立的，我们可以看到x1 x2 x4是线性独立的（因为线性方程组s λ1x1 + λ2x2 + λ4x4 = 0只可以解出 λ1 = λ2 = λ4 = 0).，因此{ x1 , x2 , x4 }是U的基。