图像去模糊：MIMO-UNet 模型详解

  本内容主要介绍实现图像去模糊的 MIMO-UNet 模型。

论文：Rethinking Coarse-to-Fine Approach in Single Image Deblurring

代码（官方）：https://github.com/chosj95/MIMO-UNet

1. 背景

  由于深度学习的成功，基于卷积神经网络（CNN）的图像去模糊方法已被广泛研究，并显示出良好的性能。基于卷积神经网络的图像去模糊模型主要分为两大类。早期，采用两阶段图像去模糊框架，即基于 CNN 的模糊核估计阶段和基于模糊核的去模糊阶段。最近，直接以端到端的方式直接学习模糊-清晰图像对之间的复杂关系，即直接从模糊图像获得清晰图像，DeepDeblur 最早使用这种方案。采用这种端到端方式的模型基本上都是采用 从粗到细（Coarse-to-fine） 策略。

  目前，从粗到细（Coarse-to-fine）策略在单图像去模糊领域已经被广泛使用。常规方案通常是通过堆叠多尺度输入图像的子网络，并从底部子网络到顶部子网络逐渐提高图像的清晰度。虽然采用从粗到细策略的网络设计在图像去模糊任务中取得了不错的性能，但是这种性能的提升是以计算复杂度和内存使用量的增加为代价的。从而导致这些模型难以用于成本和时间敏感的环境（例如移动设备、车辆和机器人等场景）。

2. 模型设计

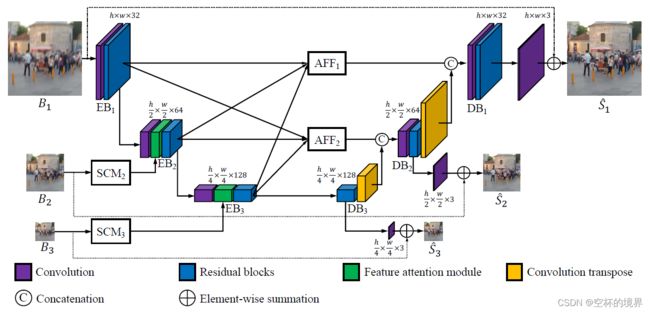
  为了实现快速并准确的去模糊网络设计，作者通过重新思考从粗到细的策略，提出了一个多输入多输出 U-net（MIMO-UNet），其架构图详见图 1.1。MIMO-UNet 是一种基于单个编码器-解码器的 U 型网络，具有三个不同的特性：

• MISE：MIMO-UNet 的单个编码器输入多尺度的输入图像，因此将其命名为多输入单编码器（Multi-input Single Encoder，MISE），以减轻训练的难度。
• MOSD：MIMO-UNet 的单个解码器输出多个不同尺度的去模糊图像，因此将其命名为多输出单解码器（Multi-output Single Decoder，MOSD）。MOSD 虽然简单，但是其可以模仿由堆叠子网络组成的常规网络架构，并指导解码器层以从粗到细的方式逐渐恢复潜在的清晰图像。
• AFF：非对称特征融合（Asymmetric Feature Fusion，AFF）有效地合并多尺度特征。AFF 输入不同尺度的特征，并合并编码器和解码器之间的多尺度信息流，以提高去模糊性能。

图 1.1 MIMO-UNet 架构图

2.1 MISE

  编码器由 3 个编码块（Encoder Block，EB）组成，具体的实现流程如下：

1. 首先，使用一个 SCM（Shallow Convolutional Module，浅卷积模块）从下采样的模糊图像中提取特征，其输出表示为 ${\text{SCM}}_k^{\text{out}}$。注意：只在第二和第三层 EB 中使用 SCM。
2. 然后，为了能够将 SCM 的输出（${\text{SCM}}_k^{\text{out}}$）与上一层 EB 的输出（${\text{EB}}_{k-1}^{\text{out}}$）进行融合，需要对 ${\text{EB}}_{k-1}^{\text{out}}$ 进行一个 stride 为 2 的卷积操作（即图 1.1 中 ${\text{EB}}_2$ 和 ${\text{EB}}_3$ 中的紫色块），得到输出 $({\text{EB}}_{k-1}^{\text{out}}{)}^{\downarrow }$，这样 ${\text{SCM}}_k^{\text{out}}$ 和 $({\text{EB}}_{k-1}^{\text{out}}{)}^{\downarrow }$ 维度相同了。注意：由于第一层没有使用 SCM，所以 ${\text{EB}}_1$ 中紫色卷积块的 stride 为 1。
3. 接着，将 ${\text{SCM}}_k^{\text{out}}$ 和 $({\text{EB}}_{k-1}^{\text{out}}{)}^{\downarrow }$ 一起输入到一个 FAM（Feature Attention Module）中（即图 1.1 中 ${\text{EB}}_2$ 和 ${\text{EB}}_3$ 中的绿色块）。注意：只在第二和第三层使用 FAM。
4. 最后，将 FAM 的输出送入到堆叠残差块中（即图 1.1 中 ${\text{EB}}_1$、${\text{EB}}_2$ 和 ${\text{EB}}_3$ 中的蓝色块）。每个残差块由 2 个 3 x 3 的卷积层组成。MIMO-UNet 堆叠 8 个这样的残差块，MIMO-UNet+ 堆叠 20 个这样的残差块。

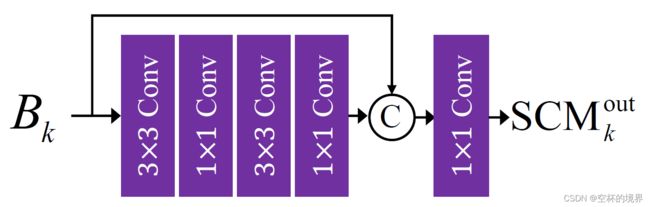
2.1.1 SCM

  SCM（Shallow Convolutional Module，浅卷积模块） 用于从下采样图像中提取特征。其结构图详见图 1.2，具体的实现流程如下：

1. 首先，堆叠两组 3 x 3 和 1 x 1 的卷积层。
2. 然后，将上一步的输出与 SCM 的输入进行拼接。
3. 最后，再连接一个 1 x 1 的卷积层。

图 1.2 SCM 结构图

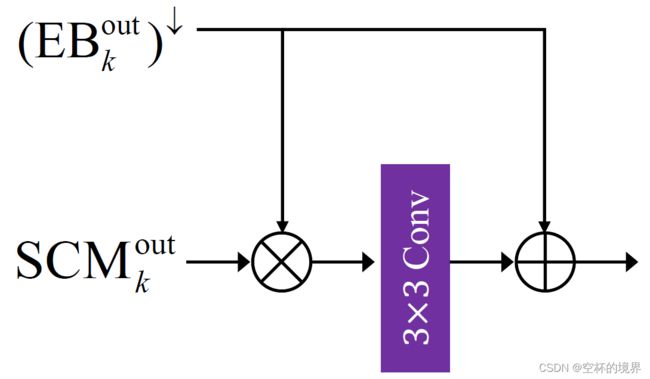
2.1.2 FAM

  FAM（Feature Attention Module，特征注意力模块） 用来强调或抑制先前尺度（也就是上一层 EB 的输出）的特征，并从 SCM 中学习特征的空间、通道重要性。结构图详见图 1.3，具体的实现流程如下：

1. 首先，将 $({\text{EB}}_{k-1}^{\text{out}}{)}^{\downarrow }$ 和 ${\text{SCM}}_k^{\text{out}}$ 按元素相乘。（需要注意一下，原论文中 FAM 结构图（即图 1.3）中，标注的 $({\text{EB}}_k^{\text{out}}{)}^{\downarrow }$ 是不正确的。）
2. 然后，将上一步的输出传入一个 3 x 3 的卷积层。
3. 最后，将上一步卷积层的输出与 $({\text{EB}}_{k-1}^{\text{out}}{)}^{\downarrow }$ 进行一个残差连接。

图 1.3 FAM 结构图

2.2 AFF

  为了在单个 U-Net 中实现不同尺度之间的信息流，作者提出了 AFF（Asymmetric Feature Fusion，非对称特征融合）。结构图详见图 1.4，具体的实现流程如下：

1. 首先，将 3 个 EB 的输出特征进行 resize。
2. 然后，将上一步 resize 后的特征进行拼接。
3. 最后，使用卷积层对拼接后的特征进行融合（一个 1 x 1 和 一个 3 x 3 的卷积层）。

图 1.4 AFF 结构图

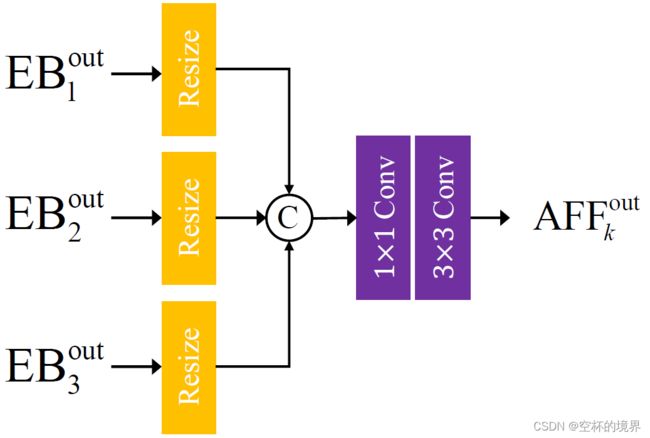
  每个 AFF 都能够接收所有编码块（EB）的输出作为输入。需要注意的是，每个 AFF 中 resize 后向量的维度是不一样的，具体计算公式如式（1.1）所示：

$$\begin{gathered} {\text{AFF}}_1^{\text{out}}={\text{AFF}}_1({\text{EB}}_1^{\text{out}},({\text{EB}}_2^{\text{out}}{)}^{\uparrow },({\text{EB}}_3^{\text{out}}{)}^{\uparrow }) \\ {\text{AFF}}_2^{\text{out}}={\text{AFF}}_2(({\text{EB}}_1^{\text{out}}{)}^{\downarrow },{\text{EB}}_2^{\text{out}},({\text{EB}}_3^{\text{out}}{)}^{\uparrow })\text{\hspace{1em}(1.1)} \end{gathered}$$

其中，${\text{AFF}}_n^{\text{out}}$ 表示第 $n$ 个 AFF 的输出。使用上采样（$\uparrow$）和下采样（$\downarrow$）是为了便于不同尺度的特征进行融合。MIMO-UNet 的每个解码块（DB）都能利用多尺度特征，从而提升模型去模糊的性能。

2.3 MOSD

  解码器也是由 3 个解码块（Decoder Block，DB）组成，具体的实现流程如下：

1. 首先，将 AFF 的输出（${\text{AFF}}_n^{\text{out}}$）与下一层 DB 的输出进行拼接。注意：只在${\text{DB}}_1$ 和 ${\text{DB}}_2$ 中有这个操作。
2. 然后，将上一步拼接后的输出连接一个 1 x 1 的卷积（即图 1.1 中 ${\text{DB}}_1$ 和 ${\text{DB}}_2$ 中的第一个紫色块），进行一下特征融合。注意：只在${\text{DB}}_1$ 和 ${\text{DB}}_2$ 中有这个操作。
3. 接着，将上一步的输出送入到堆叠残差块中（即图 1.1 中 ${\text{DB}}_1$、${\text{DB}}_2$ 和 ${\text{DB}}_3$ 中的蓝色块），其组成和 EB 中的残差块一样。
4. 再次，连接一个转置卷积（即 ${\text{DB}}_2$ 和 ${\text{DB}}_3$ 中的黄色块），实现上采样效果。这样操作是为了将其输入到上一层 DB 后，能够与 AFF 的输出（${\text{AFF}}_n^{\text{out}}$）进行拼接融合。注意：只在 ${\text{DB}}_2$ 和 ${\text{DB}}_3$ 中有这个操作。
5. 最后，在每个 DB 中，第三步的残差块的输出都会连接一个 3 x 3 的卷积层，其输出通道为 3。这样操作是为了输出不同尺度的清晰图像。注意：在进行推理的时候，${\text{DB}}_2$ 和 ${\text{DB}}_3$ 中的这个操作是可以不用进行的。

  上面的实现流程，通过公式表示如式（1.2）所示：

$${\hat{S}}_n=\{\begin{array}{cc}o({\text{DB}}_n({\text{AFF}}_n^{\text{out}};{\text{DB}}_{n+1}^{\text{out}}))+B_n,& n=1,2\\ o({\text{DB}}_n({\text{EB}}_n^{\text{out}}))+B_n,& n=3\end{array}\text{\hspace{1em}(1.2)}$$

其中，函数 $o$ 为上面第 5 步中的卷积操作。

2.4 损失函数

  和其他多尺度去模糊网络一样，使用多尺度内容损失函数。作者发现在 MIMO-UNet 中，L1 损失比 MSE 损失的效果更好。内容损失函数定义如式（1.3）所示：

$$L_{cont}=\sum _{k=1}^K\frac{1}{t_k}||\widehat{S_k}-S_k|{|}_1\text{\hspace{1em}(1.3)}$$

其中，$K$ 是网络层级的数量（在这里是 3），$t_k$ 是所有元素的数量，除以 $t_k$ 的目的是为了进行归一化。

  研究表明，除了内容损失外的辅助损失项有助于提高模型性能。由于图像去模糊的目的是恢复丢失的高频部分，因此减少频率空间的差异是非常重要的。基于这个目的，作者提出了 MSFR（Multi-scale Frequency reconstruction，多尺度频率重建） 损失函数。MSFR 损失在频域测量多尺度真实图像和去模糊图像之间的 L1 距离，具体公式如式（1.4）所示：

$$L_{MSFR}=\sum _{k=1}^K\frac{1}{t_k}||\mathcal{F}(\widehat{S_k})-\mathcal{F}(S_k)|{|}_1\text{\hspace{1em}(1.4)}$$

其中，$\mathcal{F}$ 表示快速傅里叶变换（Fast Fourier Transform，FFT），用于将图像信号转换到频域。

  最终的损失函数如式（1.5）所示：

$$L_{total}=L_{cont}+\lambda L_{MSFR}\text{\hspace{1em}(1.5)}$$

其中 λ 为 0.1。

2.5 模型变体

  为了平衡计算复杂度和性能，作者提出以下三种变体：

• MIMO-UNet：每个 EB 和 DB 使用 8 个堆叠的残差块。
• MIMO-UNet+：每个 EB 和 DB 使用 20 个堆叠的残差块。
• MIMO-UNet++：通过对 MIMO-UNet+ 使用 几何自集成 推理出清晰图片。

  简单来说，几何自集成（Geometric self-ensemble） 就是在测试时，首先将输入的模糊图像进行翻转（flip）和旋转（rotation），从而得到多张图像；然后使用 MIMO-UNet+ 对这些图像进行去模糊，得到多张清晰图像；最后将这些清晰图像进行对应的逆变换操作，再对这些清晰图像取均值从而得到最终的清晰图像。

参考：

[1] Rethinking Coarse-to-Fine Approach in Single Image Deblurring

[2] https://github.com/chosj95/MIMO-UNet

[3] MIMO-UNet笔记

[4] MIMO-UNet | 对单幅图像去模糊中由粗到细方法的再思考

[5] Enhanced Deep Residual Networks for Single Image Super-Resolution