算法之迪杰斯特拉（dijkstra）非常详细介绍

迪杰斯特拉（dijkstra）算法是单源最短路径问题的求解方法。单源最短路径就在给出一个固定网络，指定一个原点s，一个目标点e，求这两个点之间的最短路径。举个栗子来理解一下。

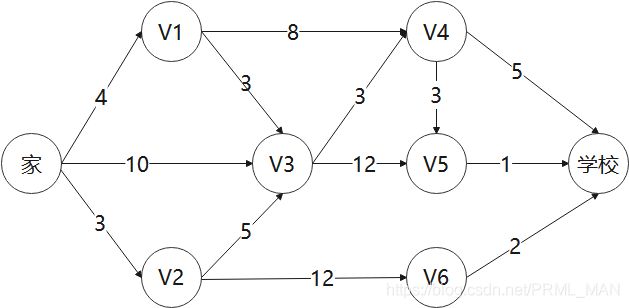
小明上学的时候，从家到学校的道路非常多，小明为了减少路上骑车的时间，因此，想找出一个最短的路径。他构造一个网络图，如下：

小明是一个很喜欢动脑筋的同学，他开始研究如何才能找出最优的路径呢？
1）所有的点到家的距离都进行初始化：

2）每次选择距离家最短的一个点，然后用这个点的距离更新其他相邻点到家的距离，如果比当前的点小，则更新节点的值。
查看所有点，V2距离家最近，则用V2更新与它相邻的点

V3: MIN(10, 3 + 5)  = 8
V6: MIN(3 + 12, INF) = 15

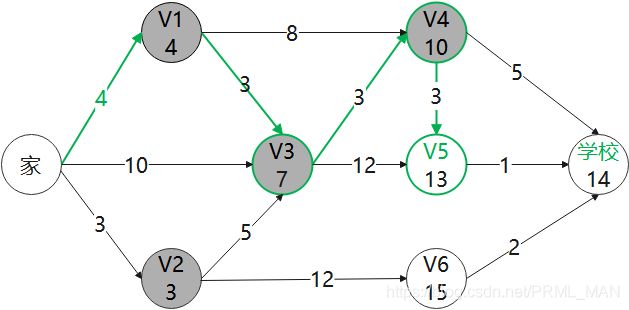
3) 剔除掉V2这个点，然后从所有点中找距离家最小值的点，发现V1最小，更新V1相连的点 V3, V4

V3: MIN(8, 4+3)  = 7
V4: MIN(4+8, INF) = 12

4)剔除掉V1这个点，继续找最小值的点 V3，更新V3相连的点 V4 V5

V4: MIN(12, 10)  = 10
V5: MIN(7 + 12, INF) = 19

5)剔除掉V3这个点，继续找最小值的点 V4，更新V4相连的点 学校和 V5

学校: MIN(10+5, INF)  = 15
V5: MIN(19, 10+3) = 13

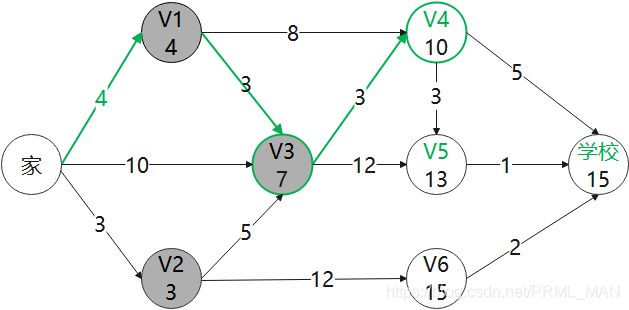
6)剔除掉V4这个点，继续找最小值的点 V5，更新V5相连的点 学校

学校: MIN(15, 13+1)  = 14

6)剔除掉V5这个点，继续找最小值的点 学校，更新学校相连的点 NULL。

到目前为止，小明找打了从家到学校的最短距离为14，经过的路径为：家-V1-V3-V4-V5-学校。

上面的整个流程就是dijkstra算法的核心思想，下面给出流程：

1）dist[]存储第i个节点到家的距离，visited[i]=true 代表第i个点是否已经遍历过。
2）遍历所有visited[i] == false的点，找出dist[i]最小的点 k。
3）遍历与k相连的点j，用 min(dist[j], dist[k] + edge[k][j])来更新 dist[j]。
4）将visited[k] = true;
5)  如果还存在点，返回2）

实例代码

练习：Dijkstra求最短路

给定一个n个点m条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出-1。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出-1。

数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。

输入样例：
3 3
1 2 2
2 3 1
1 3 4
输出样例：
3

实现代码+注释

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int edges[550][550];  // 存放所有的边，例如 edges[i][j] 代表从i到j的距离
int dist[550];  // 记录当前所有点到起点的距离
int visited[550];  // 标记当前的点是否被踢出

int dijkstra(int n, int m)
{
    for (int i = 1; i <= n; i++) {  // 每次循环都会剔除掉1个点，因此需要for循环遍历n次。
        int index = -1;  // index代表当前未被访问的距离原点最近的点
        dist[1] = 0; // 原点到原点的距离为0，这个很重要，否则下面for循环所有的dist都是0x3f3f3f3f,无法找出index。
        for (int j = 1; j <= n; j++) { // find the index of min distance 
            if (!visited[j] && (index == -1 || dist[j] < dist[index])) { // 当前的点没有被踢出，并且当前点的距离比index点的距离小，则更新index。index == -1表示还未开始找到dist中最小值，则把dist[1]加入。
                index = j;
            }
        }

        visited[index] = 1;  //找到当前距离原点最小值的点，则把点进行标记踢出。
        for (int j = 1; j <= n; j++) {
            if (dist[index] + edges[index][j] < dist[j]) { //index点更新与它相连的所有点。
                dist[j] = dist[index] + edges[index][j];
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) {  //如果没有到n点的路径，则返回-1
        return -1;
    }
    return dist[n];
}

int main()
{
    memset(edges, 0x3f, sizeof(edges));
    int n,m;
    
    scanf("%d %d", &n, &m);
    for (int i = 0; i < m; i++) {
        int start,end,d;
        scanf("%d %d %d", &start, &end, &d);
        edges[start][end] = edges[start][end] > d ? d: edges[start][end];  //因为题目输入中存在重边，所以，每次取最小值。
    }
    
    memset(dist, 0x3f, sizeof(dist));  // 初始化每个dist的值为0x3f3f3f3f， memset是按照字节来设置的，每个字节为0x3f, int四个字节，因此是 0x3f3f3f3f.
    memset(visited, 0, sizeof(visited)); // 初始化所有的点都没有被踢出。
    printf("%d\n", dijkstra(n,m));
    return 0;
}