Paddle训练yolov3 识虫小结

---

前言

第一次参加AI studio 的新手赛，还是蛮激动的。这次比赛要检测的内容本身比较简单，但是时间是真的赶，我开始做的时候只有不到一周时间。
由于之前没有参加过这类比赛，所以手头上没什么现成的资料。虽然可以从网上找，但是找的不一定符合要处理数据的格式，所以还得在原有的基础上改进，比如这次就写了个mosaic增广的函数。至于测mAP的函数到现在还每弄好，文档给的API也没法直接用。
大体说一下思路。

数据分析

数据处理部分可以直接找到源码，基本不需要改动，这里简单的对原始数据进行分析。以便搞明白我们做的任务的数据是什么样的。

名称	数量（张）
训练集	1693
验证集	245
测试集	245

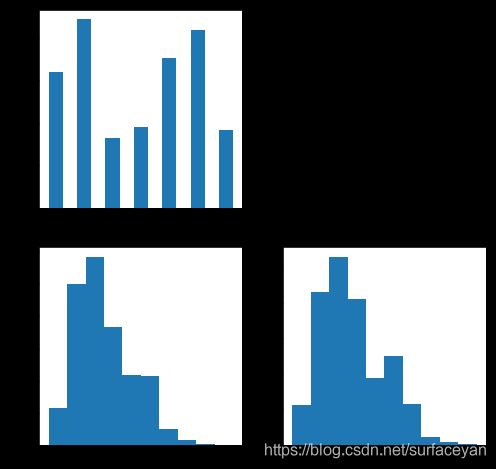
下面这张图片显示的是训练集的数据分布情况：
左上角的是统计的训练集中不同类别的真实框数量。类别还算是比较均衡。
下边两张图分别是所有方框的宽度和高度的相对值，可以看到，方框的wh大都小于0.15，所以这次检测的对象都是小目标。

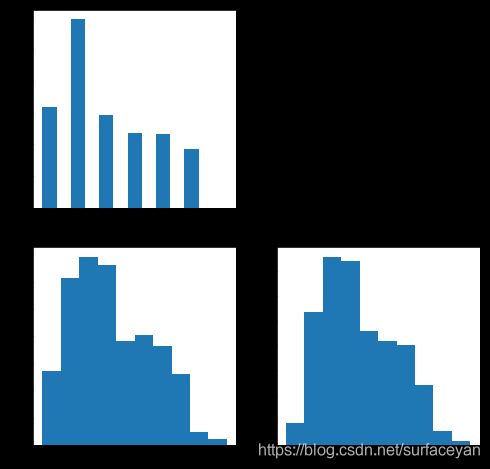
下面这张图就是验证集的统计信息了。在验证集中没有最后一个类别的框，这可能导致验证评估的时候，对最后一个类的结果不能正确评估，所以验证集可以简单的处理一下，从训练集抽取一部分包含最后一个类的真实框，随机贴到验证集的图中，从而生成新的验证集。

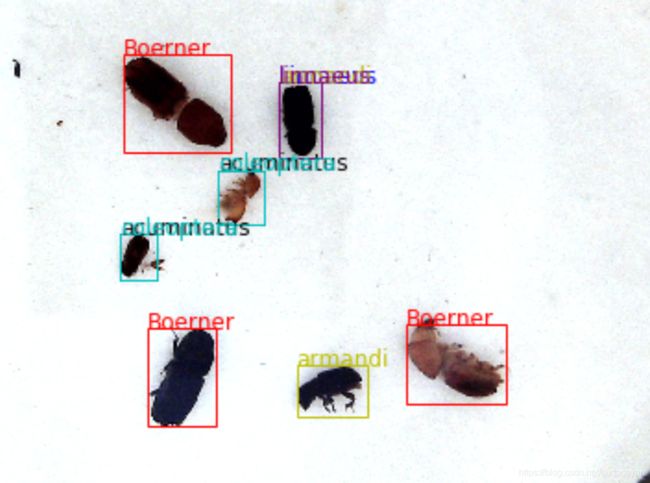
下面再来直观感受一下检测目标

训练集和测试集都是比较大的正方形的图，背景都是白色的器皿，虫子较为分散的躺在器皿内。
检测目标大都很小，所以要注重小目标的检测问题。

数据增广

在AI识虫比赛中，老师已经提供了多个数据增广的策略，包括随机色彩变换、随机填充、随机裁剪、随机缩放、随机翻转、真实框随机顺序、随机多尺度训练共七种策略，其中随机填充、随机裁剪、随机翻转需要同时对真实框进行处理，保证真实框永远与相应的物体对应。
我又添加了竖直翻转、水平竖直平移和马赛克增广方法。
据说马赛克增广可以改善小目标的检测精度。
经过处理后的数据：

附上马赛克数据增广的python源码：

#从输入的batch中随机的选择4张图片，总共选择batch次产生batch张马赛克图片
#注意batch的选取，保证每个step中的batch > 4，否则报错 raise ValueError("Sample larger than population")

# 马赛克数据增广
def merge_bboxes(img, gt_boxes, gt_labels, cutx, cuty):
    """
    gt_boxes.shape = [4, max_box, 4]
    gt_labels.shape = [4, max_box]
    img.shape = [4, C, H, W]
    以下代码还可以精简
    """
    max_box = 50 # 一张图中最大方框数，不够补零，多了截取
    cutx = cutx / img.shape[3]
    cuty = cuty / img.shape[2]

    merge_bbox = []
    merge_label = []
    for i in range(len(gt_boxes)):
        x,y,w,h = gt_boxes[i, :, 0], gt_boxes[i, :, 1], gt_boxes[i, :, 2], gt_boxes[i, :, 3]
        x1, y1, x2, y2 = x-w/2, y-h/2, x+w/2, y+h/2
        # 0 3
        # 1 2
        if i == 0:
            x1 = np.minimum(x1, cutx)
            y1 = np.minimum(y1, cuty)
            x2 = np.minimum(x2, cutx)
            y2 = np.minimum(y2, cuty)
            boolw = x2 - x1 < 0.003
            boolh = y2 - y1 < 0.003
            bool_ = boolw + boolh
            gt_labels[i][bool_] = 0
            x, y, w, h = (x1+x2)/2, (y1+y2)/2, x2-x1, y2-y1
            x[bool_] = 0
            y[bool_] = 0
            w[bool_] = 0
            h[bool_] = 0

            
        if i == 1:
            x1 = np.minimum(x1, cutx)
            y1 = np.maximum(y1, cuty)
            x2 = np.minimum(x2, cutx)
            y2 = np.maximum(y2, cuty)
            boolw = x2 - x1 < 0.003
            boolh = y2 - y1 < 0.003
            bool_ = boolw + boolh
            gt_labels[i][bool_] = 0
            x, y, w, h = (x1+x2)/2, (y1+y2)/2, x2-x1, y2-y1
            x[bool_] = 0
            y[bool_] = 0
            w[bool_] = 0
            h[bool_] = 0

        if i == 2:
            x1 = np.maximum(x1, cutx)
            y1 = np.maximum(y1, cuty)
            x2 = np.maximum(x2, cutx)
            y2 = np.maximum(y2, cuty)
            boolw = x2 - x1 < 0.003
            boolh = y2 - y1 < 0.003
            bool_ = boolw + boolh
            gt_labels[i][bool_] = 0
            x, y, w, h = (x1+x2)/2, (y1+y2)/2, x2-x1, y2-y1
            x[bool_] = 0
            y[bool_] = 0
            w[bool_] = 0
            h[bool_] = 0

        if i == 3:
            x1 = np.maximum(x1, cutx)
            y1 = np.minimum(y1, cuty)
            x2 = np.maximum(x2, cutx)
            y2 = np.minimum(y2, cuty)
            boolw = x2 - x1 < 0.003
            boolh = y2 - y1 < 0.003
            bool_ = boolw + boolh
            gt_labels[i][bool_] = 0
            x, y, w, h = (x1+x2)/2, (y1+y2)/2, x2-x1, y2-y1
            x[bool_] = 0
            y[bool_] = 0
            w[bool_] = 0
            h[bool_] = 0

        gt_boxes[i,:,0] = x
        gt_boxes[i,:,1] = y
        gt_boxes[i,:,2] = w
        gt_boxes[i,:,3] = h
    
    #TO DO:eliminate small boxes
    #may be no boxes
    #合并所有非0的box
    for i in range(len(gt_boxes)):
        for idx,box  in enumerate(gt_boxes[i]):
            if box[2]!=0 and box[3]!=0:
                merge_bbox.append(box)
                merge_label.append(gt_labels[i,idx])
    merge_bbox = np.array(merge_bbox)
    merge_label = np.array(merge_label)
    if len(merge_bbox) == 0:
        return np.zeros((max_box, 4), dtype='float32'), np.zeros((max_box,), dtype='int32')
    if len(merge_bbox) < max_box: #
        outs1 = np.zeros((max_box, 4), dtype='float32')
        outs1[:len(merge_bbox), :] = merge_bbox
        outs2 = np.zeros((max_box,), dtype='int32')
        outs2[:len(merge_bbox)] = merge_label
        return outs1, outs2
    else:
        return merge_bbox[:max_box], merge_label[:max_box]

def mosaic(img, gt_boxes, gt_labels): # 
    """
    对接
    for i, data in enumerate(train_loader()):
        img, gt_boxes, gt_labels, img_scale = data 
        img, gt_boxes, gt_labels = mosaic(img, gt_boxes, gt_labels)
    img.shape = [N, C, H, W]
    gt_boxes.shape = [N, max_len, 4]
    gt_labels = [N, max_box ]
    """
    n = len(img)
    cut_x, cut_y = [0]*n, [0]*n
    random_index = np.random.rand() * 0.3 + 0.35

    min_offset = 0.2

    for i in range(n):
        h = img.shape[2]
        w = img.shape[3]
        cut_x[i] = np.random.randint(int(w*min_offset), int(w*(1 - min_offset)))
        cut_y[i] = np.random.randint(int(h*min_offset), int(h*(1 - min_offset)))
        #cut_x[i] = random.uniform(min_offset, (1-min_offset))
        #cut_y[i] = random.uniform(min_offset, (1-min_offset))

    augmentation_calculated, gaussian_noise = 0, 0

    def get_random_imgs():
        random_index = random.sample(list(range(n)), 4) # 4张图片混合
        mosaic_img = []
        mosaic_gt_boxes = []
        mosaic_gt_labels = []
        for idx in random_index:
            mosaic_img.append(img[idx])
            mosaic_gt_boxes.append(gt_boxes[idx])
            mosaic_gt_labels.append(gt_labels[idx])
        return np.array(mosaic_img).astype('float32'), \
               np.array(mosaic_gt_boxes).astype('float32'), np.array(mosaic_gt_labels).astype('int32')
    # n images per batch, we also generate n images if mosaic
    dest = []
    new_boxes = []
    new_labels = []
    for i in range(n):
        mosaic_img, mosaic_gt_boxes, mosaic_gt_labels = get_random_imgs()
        img0 = mosaic_img[0]
        img1 = mosaic_img[1]
        img2 = mosaic_img[2]
        img3 = mosaic_img[3]

        #cut and adjust
        d1 = img0[ :, :cut_y[i], :cut_x[i] ]
        d2 = img1[ :, cut_y[i]:, :cut_x[i] ]
        d3 = img2[ :, cut_y[i]:, cut_x[i]: ]
        d4 = img3[ :, :cut_y[i], cut_x[i]: ]

        tmp1 = np.concatenate([d1, d2], axis=1)
        tmp2 = np.concatenate([d4, d3], axis=1)

        dest.append(np.concatenate([tmp1, tmp2], axis=2))
        #print(bboxes)

        tmp_boxes, tmp_labels = merge_bboxes(mosaic_img, mosaic_gt_boxes, mosaic_gt_labels, cut_x[i], cut_y[i])
        
        new_boxes.append(tmp_boxes)
        new_labels.append(tmp_labels)
        
    dest = np.array(dest).astype('float32')
    new_boxes = np.array(new_boxes).astype('float32')
    new_labels = np.array(new_labels).astype('int32')
    
    return dest, new_boxes, new_labels

网络结构

YOLO的网络可分为 backbone、neck和prediction三部分：
下面这张图是YOLOV4中的：

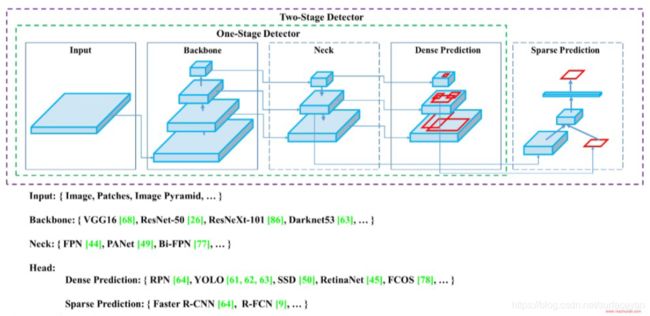
我们可以对网络中的每个部分分别进行优化，尝试更为优秀的网络结构，尤其可以先尝试哪些对小目标检测效果好的网络。
听说有人把darknet53换成了ResNet50-vd可以提高n个百分点。
我将YOLOv3的骨干网络换成了resnet50
此时需要将输出结果改成和原来的darknet53一样的格式，原来的格式：

查看一下resnet50的输出结果：

import numpy as np
with fluid.dygraph.guard():
    backbone = ResNet()
    x = np.random.randn(1, 3, 640, 640).astype('float32')
    x = fluid.dygraph.to_variable(x)
    y = backbone(x)
    print(y.shape) # [1, 1] 结果不符合要求

# 将forwar方法改成：
def forward(self, inputs):
        outs = []
        y = self.conv(inputs)
        y = self.pool2d_max(y)
        for i, bottleneck_block in enumerate(self.bottleneck_block_list):
            y = bottleneck_block(y)
            # print(i, y.shape)
            if i == 6 or i == 9 or i == 15:
                outs.append(y)
        # y = self.pool2d_avg(y)
        # y = fluid.layers.reshape(y, [y.shape[0], -1])
        # y = self.out(y)
        # print(len(self.bottleneck_block_list))
        return outs[2], outs[1], outs[0] # 将C0, C1, C2作为返回值

我把残差块的顺序调了调，使之看上去更为合理

之后更改通道数

此时resnet50的输出格式和原来的darknet53格式相同。
将原来的骨干网络部分注释掉一部分，将resnet50代码copy进去，再改改错误应该就能正常用了。

训练技巧

Mish激活函数

yolov3中用的激活函数是leak_relu，这个函数相对relu提高并不明显。

人们对激活函数的研究一直没有停止过，ReLU还是统治着深度学习的激活函数，不过，这种情况有可能会被Mish改变。 Diganta
Misra的一篇题为“Mish: A Self Regularized Non-Monotonic Neural Activation
Function”的新论文介绍了一个新的深度学习激活函数，该函数在最终准确度上比Swish(+.494%)和ReLU(+
1.671%)都有提高。
https://blog.csdn.net/u011984148/article/details/101444274

再结合前几个月发布的YOLOv4也使用了Mish激活，用mish似乎是个不错的选择，可以尝试将原来的leak_relu替换成mish。

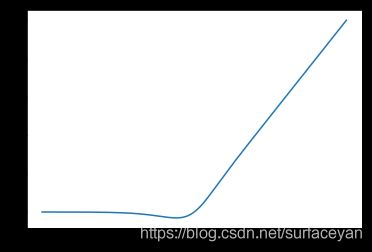
这个函数和relu很像，但解决了0点不可导的问题。

with fluid.dygraph.guard():
    x = fluid.layers.linspace(-10, 10, 1000, dtype='float32')
    mish = x * fluid.layers.tanh( fluid.layers.log( 1 + fluid.layers.exp(x) ) )

学习率调整策略

总结一下就是，在开始训练的时候用linear_lr_warmup，可以使初期网络训练更加稳定；在中期用piecewise_decay；在后期使用余弦衰减策略，不仅可以让学习率变化更加平滑，还能提供周期性变化的学习率，使网络跳出局部最优。
当然，凡事无绝对，实际上还有很多的学习率衰减策略，这需要“具体问题具体分析“。

#前期
warmup_steps = 50
start_lr = 1. / 3.
end_lr = 0.1
decayed_lr = fluid.layers.linear_lr_warmup(learning_rate,
    warmup_steps, start_lr, end_lr)
#中期
boundaries = [1000, 2000]
lr_steps = [0.1, 0.01, 0.001]
learning_rate = fluid.layers.piecewise_decay(boundaries, lr_steps) 
#后期
lr = fluid.layers.cosine_decay( learning_rate = , step_each_epoch = , epochs = )

对预测结果的改进

当网络已经够训练的良好的时候可以对预测的一些参数做一些调整。
我们的测试集中的虫子数不超过20个，可以适当的调整预测框的个数，提高丢去阈值，去掉得分过低的框。
另外，两个虫子之间框的iou不可能很大，不存在两条虫子叠加在一起的情况，此时可以适当调整multi class nms的阈值，去掉多余的重复框，以及给最后的结果添加不同类别高iou值框去除的函数。
为了进一步提高分类准确率，可以单独训练一个分类网络用于分类框选中的物体类别。
尝试多模型融合提升准确率。
另外再提一下，multi class nms算法存在一个问题，如图：
如果一个框中有多个类别的预测概率都很高，那么这个框可能会被重复使用。当然理论上一个训练良好的网络不应该出现这种情况，但现实是残酷的，它就会有这种情况，这时候单独训练的分类网络就起了作用。

对YOLO的一些思考

yolo和下面的检测方法有些相似。

https://blog.csdn.net/surfaceyan/article/details/108085893

如果恰巧有个分类网络A，他的输入尺寸也是 32 × 32，输出是维度为c的向量。
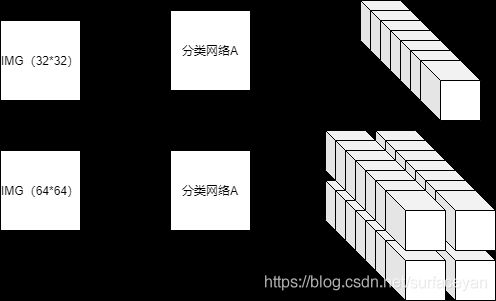
如下图，我把分类网络A的输出画成了[1 * 1 * c]的格式，图中每个小方格代表一个数。
当输入为 [32, 32]时，输出为[1,1,c]， 当输入为[64, 64]时，输出为[2,2,c] ；
当输入为 [608, 608]时，输出为[19,19,c]， 如果我们让这个分类网络对同一张图预测3次，把结果合并，那么输出为[19,19,3,c]。如果我们让它预测出c+5个类别而不是c各类别，那么它的输出就变成了 [19, 19, 3, c+5]，如果规定[h,w, i, 4：]代表预测的类别概率，[h,w, i, 4]代表这张图中有没有要分类的物体，[h,w, i, ：3]代表某种回归，那么。。。这不就是YOLO吗。。。

如果把yolo看成一个分类的网络，那么它输入图像的尺寸应该是（只考虑第一个尺度）[32 × 32]，即，感受野大小。
如果我们把输入图像划分的小方格输入到yolo网络中应该会得到该方格对应的类别概率，objectness等，但实际上输入一个放格和一张图片是完全不同的，应为邻近的方格之间会相互影响，最终影响到输出。
（部分内容剧烈变化，几乎对结果没影响；部分内容稍稍一变，对结果产生较大影响。我们要找的就是这种复杂的计算网络。）

总结