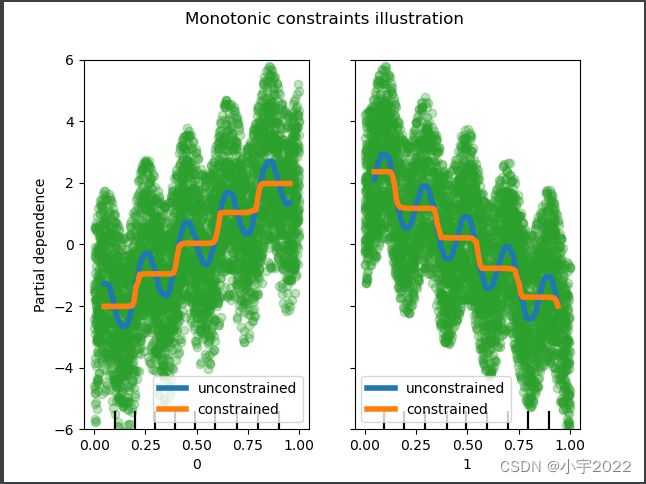
python学习之Monotonic约束绘制和【R语言】基础知识|apply函数家族中的兄弟姐妹

from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.inspection import PartialDependenceDisplay
import numpy as np
import matplotlib.pyplot as plt


rng = np.random.RandomState(0)

n_samples = 5000
f_0 = rng.rand(n_samples)  # positive correlation with y
f_1 = rng.rand(n_samples)  # negative correlation with y
X = np.c_[f_0, f_1]
noise = rng.normal(loc=0.0, scale=0.01, size=n_samples)
y = 5 * f_0 + np.sin(10 * np.pi * f_0) - 5 * f_1 - np.cos(10 * np.pi * f_1) + noise

fig, ax = plt.subplots()


# Without any constraint
gbdt = HistGradientBoostingRegressor()
gbdt.fit(X, y)
disp = PartialDependenceDisplay.from_estimator(
    gbdt,
    X,
    features=[0, 1],
    line_kw={"linewidth": 4, "label": "unconstrained", "color": "tab:blue"},
    ax=ax,
)

# With positive and negative constraints
gbdt = HistGradientBoostingRegressor(monotonic_cst=[1, -1])
gbdt.fit(X, y)

PartialDependenceDisplay.from_estimator(
    gbdt,
    X,
    features=[0, 1],
    feature_names=(
        "First feature\nPositive constraint",
        "Second feature\nNegtive constraint",
    ),
    line_kw={"linewidth": 4, "label": "constrained", "color": "tab:orange"},
    ax=disp.axes_,
)

for f_idx in (0, 1):
    disp.axes_[0, f_idx].plot(
        X[:, f_idx], y, "o", alpha=0.3, zorder=-1, color="tab:green"
    )
    disp.axes_[0, f_idx].set_ylim(-6, 6)

plt.legend()
fig.suptitle("Monotonic constraints illustration")

plt.show()

01

apply()

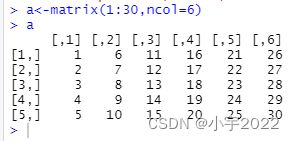
这个函数是对数组，矩阵或数据框的一个变量使用函数生成列表或者数组/向量。

apply(x,MARGIN ,fun,….)

x是数据对象，类型可以为数组/矩阵/数据框。

MARGIN表示矩阵的行与列，MARGIN=1表示矩阵行，MARGIN=2表示矩阵列。

#例子1

02

lapply()

lapply(x,FUN,….)

x是数据对象，类型可以为向量/列表/数据框。

FUN是指使用的函数。

03

sapply()

sapply(x,FUN…,simplify=TRUE,USE.MAMES=TRUE)

simplify=TRUE表示将lappy输出的list简化为向量vector或者矩阵matrix

04

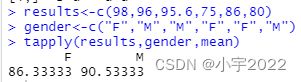
tapply()

使用的格式：

tapply(x,INDEX，FUN，…，simplify=TRUE)

x：数据类型是向量

INDEX：因子列表，而且长度和x一样，如果INDEX不是因子，tapply（）函数依然能够运行，R会把非因子用as.factor（）强制将其转为因子。

simplify：逻辑值为TRUE表示计算的结果返回的是数组。若逻辑词是FALSE，计算的结果返回的是列表对象。

tapply函数可以根据分组进行统计。

05

mapply()

mapply(FUN,MoreArgs=NULL,SIMPLIFY=TRUE,USE.NAMES=TRUE)

SIMPLIFY表示逻辑词，SIMPLIFY=TRUE时，能够把结果转变为向量/矩阵/高维阵列。

MoreArgs是FUN函数的其他参数的列表。

#使用mapply函数重复生成列表list(x=3:6),重复次数times=1:4,而且生成的结果是列表。

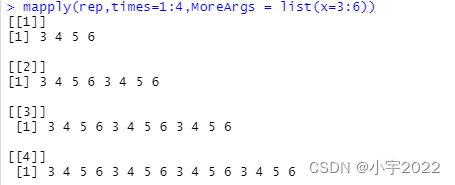
#使用mapply函数重复生成列表list(x=3:6),重复次数times=1:4,而且生成的结果是矩阵。