中心极限与大数定理律的关系_21厦大数学考研 | 数列与函数极限复习建议!
时间已经到了10月了
很快就要进入11月冲刺阶段
关于数列极限你们搞清楚了吗?
还有不懂的?
学姐来为你解答
小满师姐:总分340+(分数线310),专业课数学分析120+。连续3年从事考研专业课辅导工作。
曾担任本科教学助理并参与评阅试卷,在厦大做科研助理一年,期间参与科研项目、论文及专利写作,编写数学建模比赛培训教案及编程python实现案例。
参与中国运筹学会金融工程与金融风险管理分会第六届学术年会,并在年会上发表学术报告。
数列极限
在数列极限这一章中,首先,引入了基本的极限的定义、性质及四则运算之后,教材中介绍了至少6个求极限的方法。
随后,有了收敛的性质,知道了收敛数列有什么特性,比如说收敛的有界性,也就是收敛必有界,定理2.2.2(这个是判断收敛的必要条件)。
那么反过来,有界数列必收敛吗?
不一定吧,举个反例,sin(n*\pi/4).我们更想知道收敛数列的充要条件,这跟一个数列本身的性质有关。
为什么要找到收敛数列的充要条件呀?
如果只根据收敛的定义,很多时候我们甚至不知道它的极限,要是没有别的判断方法就无法知道其是不是收敛。
一个自然的想法是,既然收敛必有界,有界不一定收敛。那么肯定有界与收敛存在一个相关的关系,我们已经猜对了一半了吧。
那自然的就有几个问题:
l 有界数列加上什么条件,就必定收敛(判断收敛的充分条件):单调有界数列收敛定理
l 有界数列可以得到什么结论?(虽然不一定收敛,应该是一个弱一点的结论也没关系):Bolzano-Weierstrass定理
l 更进一步地,判断收敛的充要条件是什么呢?:Cauchy收敛原理
闭区间套定理把这4个定理建立了联系。
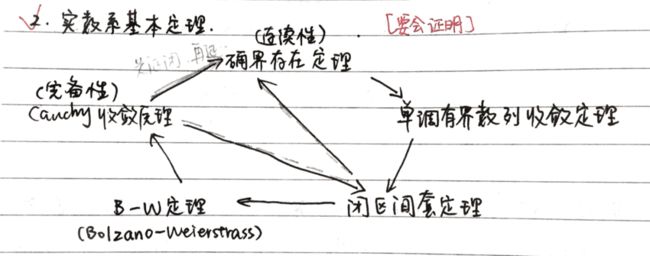
在数列极限这一章中,五个实数系的基本定理需要掌握其证明,其5个定理的关系如下图所示:
1. 确界存在定理(实数系连续性):非空有上界数集必有上确界。证:刻画
2. 单调有界数列收敛定理。证:确界存在定理及确界定义
3. 闭区间套定理:闭区间套,存在唯一实数属于所有闭区间,且唯一。证:存在性,单调有界收敛定理及闭区间套定义;唯一性,反证及夹逼
4. B-W定理:有界数列必有收敛子列。证:构造闭区间套得极限,再证有一子列收敛于该极限(构造一子列夹逼于闭区间两端点)
5. Cauchy收敛原理(实数系完备性):数列收敛得充要条件是基本数列。证:必要,收敛定义及插项三角不等式;充分,基本数列定义知必有界,由B-W定理知有收敛子列趋于极限,基本数列定义
第二点需要掌握的是,求极限的常见方法。
现给大家总结如下:
1. 由定义解出最佳正整数N,注意插项和三角不等式的技巧;
2. 利用二项式放缩,注意典型题型及常见结论;
3. 两个平均值;
4. 夹逼准则;
5. Stolz定理,思考什么时候用Stolz定理:如有明显递推、给出和式时;
6. 应用单调有界数列收敛定理;
(1) 利用递推求极限
(2) 三个常用无理数
(3) p级数
(4) Fibonaccii数列
函数极限
函数极限的大部分定义定理为数列极限的延拓,大家复习时应注意对比。
同时,要明白连续其实本质上就是极限,也要会区分点连续和一致连续:前者为局部性,后者则为整体性的概念。
另外,连续函数中的重点为三类不连续点,对应不同的类型应能给出典型例子,并画图形象表示,可以判断不连续点的类型。
(1)第一类(跳跃点):左右极限存在但不相等。注意单调函数;
(2)第二类:左右极限中有不存在。注意Dirichlet函数及其变形;
(3)第三类(可去间断点):左右极限存在且相等,但不等于f(x0)或f(x0)无定义。
例f(x)=xsin(1/x);注意例3.2.7 Riemann函数(画图直观理解,对比Riemann函数和dirichlet函数,一个跳的高度一样,一个跳的高度为1/p)。
在无穷小量与无穷大量的阶这一小节中,需自己总结常用的等价关系。
例如我总结的部分常用等价关系和高阶关系给大家参考一下。
【参考】
l 常用的等价关系:
1)x->0:
sinx~x
1-cosx~1/2 x^2
tanx - sinx ~ 1/2 x^3 ,变形 sinx ((1-cosx)/cosx) ~ 1/2 x^3
In(1+x) ~ x
(1+x)^a -1 ~ ax
tanx ~ x
arctanx ~ x
e^x - 1 ~ x,变形 a^x -1 ~ x Ina
2)x->\pi/2 -:
tanx ~ 1/(\pi/2 - x),变形如下
cosx ~ \pi/2 - x
l 常用的高阶关系:
1)x->+\infty:低到高阶无穷大量(从小到大)
In^k(x), x^a, a^x,[x]!,x^x
2)x->0+:高到低阶无穷小量(从小到大)
(1/x)^(-1/x), 1/[1/x]!, a^(-1/x), x^a, In^(-k)(1/x)
随后,对于连续函数在闭区间上的5个分析性质,对应5个定理:有界性定理、最值定理、零点存在定理、一致连续Cantor定理,需掌握其证明思想。
证明它们用了实数系的5个基本定理,当中我们用的比较多的是b-w定理和闭区间套定理,实际上因为实数系的5个基本定理等价,因此用任意一个证明都是等价的,难度有差。这种题可以考,可当作习题自我检测。
综 述
l 函数极限要跟数列极限的相关概念、定理和方法对比,课上我有提出来哪个证明方法其实跟哪个定理是一样的,哪个定理其实是谁的拓展版,哪个概念其实就是哪个概念。类似这样的问题帮助你看清楚知识点的本质,加深你对这个知识点的认识。总之多对比,多总结。
l 跟数列极限一起复习,找到框架性的知识,比如数列极限和函数极限分别讲了它们的什么性质,分别有什么关系,要有框架性的大纲,学数学要时刻清楚自己在干什么,目标要明确。有的时候某一步很难过来推不下来,会卡住,但弄明白这种细枝末节的步骤以后也要学会跳出细节,了解框架。
l 不断对比总结,框架上一层一层拔高一个层次、越来越高的角度来理解,来总结,这样做笔记对你们帮助会非常大。
21届考研初试辅导班招生进行中... 大家有任何疑问 入群 或 加微信,一对一咨询注:图片来源于网络,版权归原作者所有,侵删。
录取分数线、参考书目、真题分析、提分技巧!