支持向量机SVM-人脸识别
SVM向量机算法原理
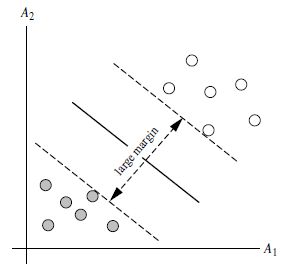
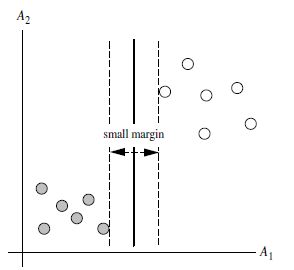
SVM寻找区分两类的超平面(hyper plane), 使边际(margin)最大
线性可分SVM——线性 SVM——非线性 SVM
1、线性可分SVM,表示可以用一根线非常清晰的划分两个区域;线到支持向量的距离 d 就是最小的。
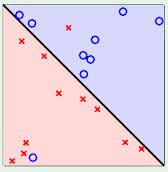
2、线性 SVM,表示用一根线划分区域后,可能存在误判点,但还是线性的;线到支持向量的距离不一定是最小的,但忽略其他非规则的支持向量。
3、非线性 SVM,表示使用核函数之后,把低维的非线性转换为高维线性
线性可区分
线性不可区分的情况
SVM推导
最初分类函数、最大化margin、拉格朗日
SVM推导过程同样分为线性与非线性
线性可分支持向量机
SVM利用间隔最大化求得最优超平面,解唯一。其分类决策函数为
f ( x ) = s i g n ( w ⋅ x + b ) f(x)=sign(w⋅x+b) f(x)=sign(w⋅x+b)
非线性可分支持向量机
在计算得到核函数之前,需要完成两步:
1.首先使用一个非线性映射将数据变换到一个特征空间F;
2. 然后在特征空间使用线性学习器分类;
其分类决策函数为
f ( x ) = ∑ i = 1 N w i ⋅ Φ ( x i ) + b f(x) = \sum_{i=1}^{N} w_i \cdot \Phi(x_i) +b f(x)=∑i=1Nwi⋅Φ(xi)+b
其中 Φ ( x i ) \Phi(x_i) Φ(xi)就是将样本映射到高维空间的映射函数。
支持向量机代码
需要的模型
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report
from sklearn.svm import SVC
from sklearn.decomposition import PCA
train_test_split是用来分割数据集的,将数据分为训练数据和测试数据
fetch_lfw_people就是我们用到的人脸数据集
GridSearchCV是寻找合适的SVM参数组合的
classfusion_report和confusion_matrix是后面用来给模型打分的
RandomizedPCA就是我们用来降维的
数据
# 下载数据集--户外脸部数据集lfw(Labeled Faces in the Wild)
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
# 函数定义
Signature: fetch_lfw_people(data_home=None, funneled=True, resize=0.5, min_faces_per_person=0, color=False, slice_=(slice(70, 195, None), slice(78, 172, None)), download_if_missing=True)
Docstring:
Loader for the Labeled Faces in the Wild (LFW) people dataset
# minfaces_per_person:int,可选默认无,提取的数据集仅保留包含min_faces_per_person不同图片的人的照片
# resize调整每张人脸图片的比例,默认是0.5
显示图片以及数据格式
plt.imshow(lfw_people.images[6],cmap='gray')
plt.show()
n_samples, h, w = lfw_people.images.shape #实例数(图片数)、h、w
print(n_samples)
print(h)
print(w)
lfw_people.data.shape ## 图像的维度 对于图像维度较小 对于SVM算法 维度较高
#X矩阵用来装特征向量,得到数据集的所有实例
#每一行是一个实例,每一列是个特征值
X=lfw_people.data
#X矩阵调用shape返回矩阵的行数和列数,
X.shape[1] #返回矩阵的列数,对应的特征向量的维度或者特征点多少
#获取特征结果集,提取每个实例对应的每个人脸
#y为classlabel目标分类标记,即不同人的身份
lfw_people.target
target_names = lfw_people.target_names ## 类别的数量 以人名组成列表返回
target_names
n_classes = lfw_people.target_names.shape # 维度 多少行
n_classes
n_classes = n_classes[0]
n_classes
print("Total dataset size:") #数据信息
print("n_samples:%d"% n_samples) #数据个数
print("n_features:%d"% n_features) #特征个数,维度
print("n_classes:%d"% n_classes) #结果集类别个数,即多少个人
拆分数据为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lfw_people.data, lfw_people.target) # 拆分函数,可以增加test_size=0.25参数,表示随机抽取25%的测试集,还有其他参数可供选择
支持向量机SVM
model = SVC(kernel='rbf', class_weight='balanced') # 自动输出SCV的各种默认参数
model.fit(x_train, y_train)
输出
SVC(C=1.0, cache_size=200, class_weight='balanced', coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
单纯的SVM算法输出
predictions = model.predict(x_test)
print(classification_report(y_test, predictions, target_names=lfw_people.target_names))
# 相对于SVM算法较大的维度,得到的精度很低,因此需要对图像进行降维
PCA降维
# 100个维度
n_components = 100
pca = PCA(n_components=n_components, whiten=True).fit(lfw_people.data)
x_train_pca = pca.transform(x_train) # tranform对数据进行降维
x_test_pca = pca.transform(x_test)
x_train_pca.shape # 降维后的维度
再次利用SVM进行建模 得到结果
model = SVC(kernel='rbf', class_weight='balanced')
model.fit(x_train_pca, y_train)
predictions = model.predict(x_test_pca)
print(classification_report(y_test, predictions, target_names=target_names))
调参进一步优化
# 调参的方法可以通用
# 调参的方法 把参数全部设置 算法自动进行调参 'C' 'gamma' 5个参数逐个进行调参
#c是一个对错误的部分的惩罚
#gamma的参数对不同核函数有不同的表现,gamma表示使用多少比例的特征点
#使用不同的c和不同值的gamma,进行多个量的尝试,然后进行搜索,选出准确率最高模型
param_grid = {'C': [0.1, 1, 5, 10, 100],
'gamma': [0.0005, 0.001, 0.005, 0.01], }
#调用SVM进行分类搜索哪对组合产生最好的归类精确度
#ernel:rbf高斯径向基核函数 class_weight权重
#把所有我们所列参数的组合都放在SVC里面进行计算,最后看出哪一组函数的表现度最好
model = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid)
model.fit(x_train_pca, y_train)
print(model.best_estimator_)
输出结果
#进行评估准确率计算
predictions = model.predict(x_test_pca)
#通过classification_report方法进行查看,可以得到预测结果中哪些是正确
print(classification_report(y_test, predictions, target_names=target_names))
再次调参
param_grid = {'C': [0.1, 0.6, 1, 2, 3],
'gamma': [0.003, 0.004, 0.005, 0.006, 0.007], }
model = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid)
model.fit(x_train_pca, y_train)
print(model.best_estimator_)
输出结果
predictions = model.predict(x_test_pca)
print(classification_report(y_test, predictions, target_names=target_names))
最后画图,验证最终测试结果
# 画图,3行4列
#将测试标记过进行展示,即先弄一个通用的图片可视化函数:
def plot_gallery(images, titles, h, w, n_row=3, n_col=5):
#建立图作为背景
#自定义画布大小
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
#位置调整
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35) # 图片显示效果的设置
for i in range(n_row * n_col):
#设置画布划分以及图像在画布上输出的位置
plt.subplot(n_row, n_col, i + 1)
#在轴上显示图片
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
#整个画板的标题
plt.title(titles[i], size=12)
#获取或设置x、y轴的当前刻度位置和标签
plt.xticks(())
plt.yticks(())
# 获取一张图片title
#预测函数归类标签和实际归类标签打印
#返回预测人脸姓和测试人脸姓的对比title
def title(predictions, y_test, target_names, i):
#rsplit(' ',1)从右边开始以右边第一个空格为界,分成两个字符
#组成一个list
#此处代表把'姓'和'名'分开,然后把后面的姓提出来
#末尾加[-1]代表引用分割后的列表最后一个元素
#对比rsplit与split的区别
pred_name = target_names[predictions[i]].split(' ')[-1]
true_name = target_names[y_test[i]].split(' ')[-1]
return 'predicted: %s\ntrue: %s' % (pred_name, true_name)
# 获取所有图片title
prediction_titles = [title(predictions, y_test, target_names, i) for i in range(len(predictions))] # list中的循环
# 画图
plot_gallery(x_test, prediction_titles, h, w)
#打印原图和预测的信息
eigenface_titles =["eigenface %d" % i for i in range (eigenfaces.shape[0])]
#调用plot_gallery函数打印出实际是谁,预测的谁,以及提取过特征的脸
plot_gallery(eigenfaces, eigenface_titles, h, w)
plt.show()
引用博客
SVM算法详细推导过程