基本排序(4)——归并排序、计数排序
目录
前言
归并排序思路
递归代码实现
非递归代码实现
计数排序
代码实现
前言
归并排序适用于对大量数据进行排序(指超过内存存储上限的数据量,其他排序算法完全无法处理),计数排序则是另一种思路。
归并排序思路
1、将序列分为左右均等的两部分
2、递归排序左右半侧
3、最后左右半侧合并
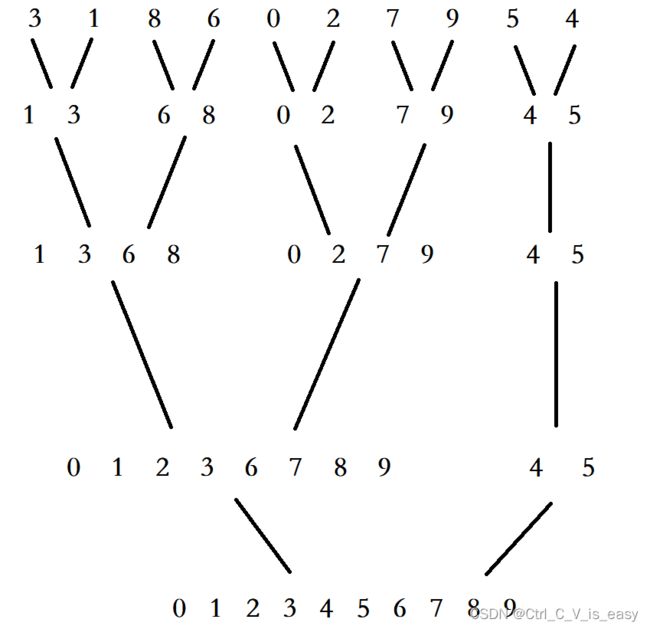
比如有一个序列: 3 1 8 6 0 2 7 9 5 4
,先用递归将序列对半分开,递归到最底层时每个部分只有2个元素做比较
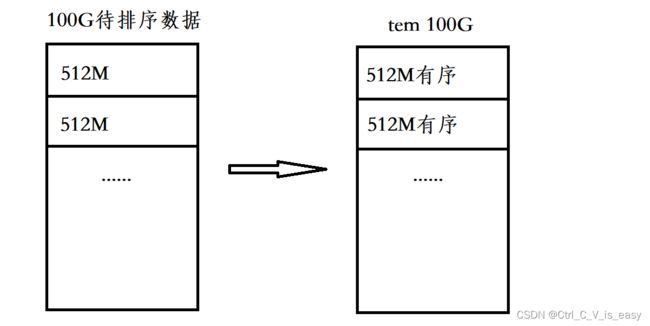
又比如我们有100G的数据需要排序,但我们的内存大小为1G,则只能用归并排序
先取一个100G容量的空间,因为内存只有1G所以就把100G数据按512M(1G的一半)分成若干份,每个部分排序,这样每个部分都有序
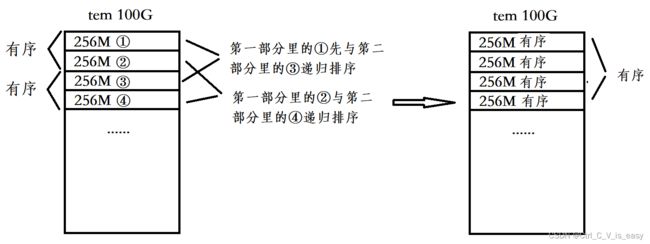
然后再把512M数据对半分开,取第一部分的①和第二部分的③来递归排序
然后再将256M对半分开重复以上操作
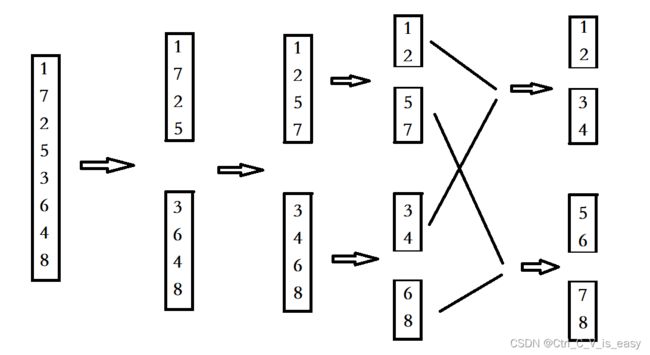
举个例子简化一下流程:
递归代码实现
void _mergesort(int *a, int left, int right, int * tem){//递归
if (left >= right)
return;
int mid = (left + right) / 2; //从中间分隔
_mergesort(a, left, mid, tem); //递归到最底层
_mergesort(a, mid + 1, right, tem);
int begin_1 = left, begin_2 = mid+1; //设置新的下标
int i = left; //注意新数组的小标要与待排序数组下标区分,i不能初始化为0
while (begin_1 <= mid && begin_2 <= right){ //将最小的先入新数组
if (a[begin_1] < a[begin_2])
tem[i++] = a[begin_1++];
else
tem[i++] = a[begin_2++];
}
while (begin_1 <= mid){ //上一步操作完后,可能还有一个数组的元素没有入新数组,将其全部放入新数组
tem[i++] = a[begin_1++];
}
while (begin_2 <= right){//
tem[i++] = a[begin_2++];
}
for (int j = left; j <= right; ++j){ //将新数组的元素拷贝到原数组,注意j <= right,而不是j < right(在这里失误了)
a[j] = tem[j];
}
}
void MergeSort(int* a, int n){ //归并排序
int *tem = (int*)malloc(sizeof(int)*n);
if (tem != NULL){
_mergesort(a, 0, n - 1, tem);
}
}非递归代码实现
void _mergesortNonR(int *a,int gap, int left, int right, int *tem){ //非递归
while (gap < (right + 1)){
for (int i = 0; i < right; i = i + gap * 2){
int begin_1 = i, end1 = i + gap - 1, mid = i + gap - 1; //设置各个下标
int begin_2 = mid + 1, end2 = i + gap * 2 - 1;
int j = i; //单独设置tem新数组的下标
if (end2>right) //当最右下标超过数组大小后,将数组最大下标赋予给end2
end2 = right;
if (begin_2 > right) //当第二部分起始下标大于数组最大下标后退出
break;
while (begin_1 <= end1 && begin_2 <= end2){
if (a[begin_1] < a[begin_2])
tem[j++] = a[begin_1++];
else
tem[j++] = a[begin_2++];
}
while (begin_1 <= end1){
tem[j++] = a[begin_1++];
}
while (begin_2 <= end2){
tem[j++] = a[begin_2++];
}
for (int k = 0; k <= end2; ++k){
a[k] = tem[k];
}
}
gap = gap * 2; //
}
}
void MergeSortNonR(int* a, int n){ //归并排序
int* tem = (int*)malloc(sizeof(int)*n);
int gap = 1;
_mergesortNonR(a,gap,0,4,tem);
}计数排序
计数排序的想法相比于其他排序真的是与众不同,他并非直接对序列进行排序,而是创建一个新数组,用这个新数组的下标来对应原序列的各个元素。这是一种用空间换时间的排序方法。
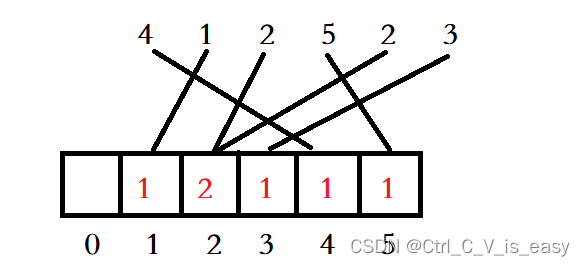
例如一个序列: 4 1 2 5 2 3,我们创建一个新数组,新数组的长度是原序列里最大元素的值加一,原序列最大元素是5,所以创建一个长度为6的新数组
新数组的下标对应原序列的每个元素,数组则用于计数
然后再用这个新数组来遍历打印即可完成排序,由此可以看出这个方法在应对原序列中有很大值的元素时会花费很多空间。
代码实现
void CountSort(int* a, int n){ //计数排序
int max = 0; //先找原数组里面的最大元素,将其作为新数组的最大下标
for (int i = 0; i < n; ++i){
if (a[i]>max)
max = a[i];
}
int *tem = (int*)malloc(sizeof(int)*(max + 1));
for (int i = 0; i <= max; ++i){//将新数组置0
tem[i] = 0;
}
for (int i = 0; i < n; ++i){
tem[a[i]]++; //将a[i]作为新数组的下标
}
int *tem_out = (int*)malloc(sizeof(int)*n);
int k = 0;
for (int i = 0; i < (max + 1); ++i){
while (tem[i]>0){ //最后输出新数组的下标到另外一个数组
tem_out[k++] = i;
tem[i]--;
}
}
for (int i = 0; i < n; ++i){
a[i] = tem_out[i]; //数组拷贝
}
}
各个排序到此基本都梳理完了。