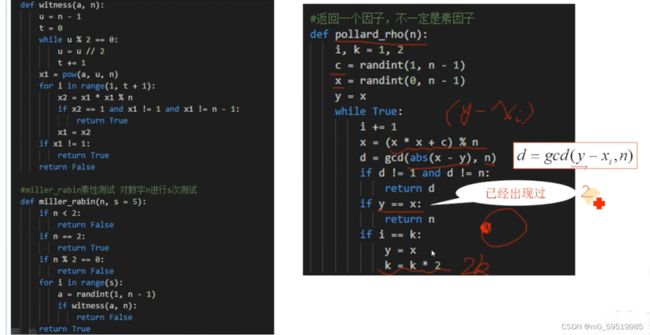
简单数论合集
质因数分解:
题目描述
已知正整数 nn 是两个不同的质数的乘积,试求出较大的那个质数。
输入描述
输入只有一行,包含一个正整数 n,6≤n≤2×109n,6≤n≤2×109。
输出描述
输出只有一行,包含一个正整数 pp,即较大的那个质数。
输入输出样例
示例
输入
21
输出
7
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
public static boolean find(int x) {
for(int i=2;i<=Math.sqrt(x);i++) {
if(x%i==0) {
return false;
}
}
return true; //是质数
}
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
int n=scan.nextInt();
scan.close();
// boolean[] a=new boolean[(int)(Math.sqrt(n)%1)];
// Arrays.fill(a, true);
// for(int i=2;i*i<=n;i++) {
// if(a[i]) {
// for(int j=i*i;j<=n;j+=i) {
// a[j]=false;
// }
// }
// }
for(int i=n;i>=Math.sqrt(n);i--) {
if(find(i)&&n%i==0) {
System.out.println(i);
return;
}
}
}
}都有两个超时
求质因子的个数
import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan=new Scanner(System.in);
int n=scan.nextInt();
scan.close();
for(int i=2;i质数:
题目描述
给定一个正整数 NN,请你输出 NN 以内(不包含 NN)的质数以及质数的个数。
输入描述
输入一行,包含一个正整数 NN。 1≤N≤1031≤N≤103
输出描述
共两行。
第 11 行包含若干个素数,每两个素数之间用一个空格隔开,素数从小到大输出。
第 22 行包含一个整数,表示N以内质数的个数。
输入输出样例
示例
输入
10
输出
2 3 5 7
4
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
import java.util.Arrays;
import java.util.Scanner;
public class 质数{
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n=scan.nextInt();
scan.close();
int sum=0;
boolean[] a=new boolean[n+1];
Arrays.fill(a,true);
for(int i=2;i*i<=n;i++) {
for(int j=i*i;j小数第n位
题目描述
我们知道,整数做除法时,有时得到有限小数,有时得到无限循环小数。
如果我们把有限小数的末尾加上无限多个 0,它们就有了统一的形式。
本题的任务是:在上面的约定下,求整数除法小数点后的第 nn 位开始的 3 位数。
输入描述
输入一行三个整数:a b na b n,用空格分开。aa 是被除数,bb 是除数,nn 是所求的小数后位置(0 输出一行 3 位数字,表示:aa 除以 bb,小数后第 nn 位开始的 3 位数字。 示例 输入 输出 仍然有一个测试用例超时 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 你一定听说过这个故事。国王对发明国际象棋的大臣很佩服,问他要什么报酬,大臣说:请在第 11 个棋盘格放 11 粒麦子,在第 22 个棋盘格放 22 粒麦子,在第 33 个棋盘格放 44 粒麦子,在第 44 个棋盘格放 88 粒麦子,......后一格的数字是前一格的两倍,直到放完所有棋盘格(国际象棋共有 6464 格)。 国王以为他只是想要一袋麦子而已,哈哈大笑。 当时的条件下无法准确计算,但估算结果令人吃惊:即使全世界都铺满麦子也不够用! 请你借助计算机准确地计算,到底需要多少粒麦子。 数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一 部分的数列,只记得其中 NN 个整数。 现在给出这 NN 个整数,小明想知道包含这 NN 个整数的最短的等差数列有几项? 输入的第一行包含一个整数 NN。 第二行包含 NN 个整数 A1,A2,⋅⋅⋅,ANA1,A2,⋅⋅⋅,AN。(注意 A1A1 ∼ ANAN 并不一定是按等差数列中的顺序给出) 其中,2≤N≤105,0≤Ai≤1092≤N≤105,0≤Ai≤109。 输出一个整数表示答案。 示例 输入 输出 样例说明: 包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、 18、20。 任何一个大于 1 的正整数都能被分解为若干个质数相乘, 比如 28=2×2×728=2×2×7 被分解为了三个质数相乘。请问在区间 [2333333, 23333333] 中有多少个正整数 可以被分解为 12 个质数相乘? 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。 约数的个数: 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 12000001200000 有多少个约数(只计算正约数)。 质数拆分: 倍数: 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 请问在 11 到 20202020 中,有多少个数既是 44 的整数倍,又是 66 的整数倍。 阶乘约数: 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 定义阶乘 n!=1×2×3×⋅⋅⋅×nn!=1×2×3×⋅⋅⋅×n。 请问 100!100! (100100 的阶乘)有多少个正约数。 质数分解定理 合数个数: 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 一个数如果除了 11 和自己还有其他约数,则称为一个合数。例如:1,2,31,2,3 不是合数,4,64,6 是合数。 请问从 1 到 2020 一共有多少个合数。 最小公倍数: 为什么 1 小时有 60 分钟,而不是 100 分钟呢?这是历史上的习惯导致。 但也并非纯粹的偶然:60 是个优秀的数字,它的因子比较多。 事实上,它是 1 至 6 的每个数字的倍数。即 1,2,3,4,5,6 都是可以除尽 60。 我们希望寻找到能除尽 1 至 nn 的的每个数字的最小整数。 不要小看这个数字,它可能十分大,比如 nn = 100, 则该数为: 69720375229712477164533808935312303556800 输入一个数字 N (N<100)N (N<100)。 输出出 1 ~ nn 的最小公倍数。 示例 输入 输出 BigInteger的使用 找素数 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 素数就是不能再进行等分的整数。比如:7,117,11。而 99 不是素数,因为它可以平分为 33 等份。一般认为最小的素数是22,接着是 3,5,...3,5,... 请问,第 100002100002(十万零二)个素数是多少? 请注意:“2”“2” 是第一素数,“3”“3” 是第二个素数,依此类推。 纯质数: 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 如果一个正整数只有 11 和它本身两个约数,则称为一个质数(又称素数)。 前几个质数是:2,3,5,7,11,13,17,19,23,29,31,37,⋅⋅⋅2,3,5,7,11,13,17,19,23,29,31,37,⋅⋅⋅ 。 如果一个质数的所有十进制数位都是质数,我们称它为纯质数。例如:2,3,5,7,23,372,3,5,7,23,37 都是纯质数,而 11,13,17,19,29,3111,13,17,19,29,31 不是纯质数。当然 1,4,351,4,35 也不是纯质数。 请问,在 11 到 2021060520210605 中,有多少个纯质数? 序列求和: 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 学习了约数后,小明对于约数很好奇,他发现,给定一个正整数 tt,总是可以找到含有 tt 个约数的整数。小明对于含有 tt 个约数的最小数非常感兴趣,并把它定义为 StSt 。 例如 S1=1,S2=2,S3=4,S4=6,⋅⋅⋅S1=1,S2=2,S3=4,S4=6,⋅⋅⋅ 。 现在小明想知道,前 6060 个 SiSi 的和是多少?即 S1+S2+⋅⋅⋅+S60S1+S2+⋅⋅⋅+S60 是多少? 核桃的数量: 小张是软件项目经理,他带领 3 个开发组。工期紧,今天都在加班呢。为鼓舞士气,小张打算给每个组发一袋核桃(据传言能补脑)。他的要求是: 各组的核桃数量必须相同 各组内必须能平分核桃(当然是不能打碎的) 尽量提供满足 1,2 条件的最小数量(节约闹革命嘛) 输入一行 a,b,ca,b,c,都是正整数,表示每个组正在加班的人数,用空格分开(a,b,c<30)(a,b,c<30)。 输出一个正整数,表示每袋核桃的数量。 示例 输入 输出输出描述
输入输出样例
1 8 1
125
运行限制
import java.util.Scanner;
public class 小数第n位{
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
long a=scan.nextLong();
long b=scan.nextLong();
long n=scan.nextLong();
scan.close();
long d=a%b;
for(int i=0;iimport java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scn = new Scanner(System.in);
int a = scn.nextInt(), b = scn.nextInt(), n = scn.nextInt();
a %= b;
// 快速幂算法求 a * 10^(n-1) % b
long base = 10;
long exponent = n - 1;
long result = 1;
while (exponent > 0) {
if (exponent % 2 == 1) {
result = (result * base) % b;
}
base = (base * base) % b;
exponent /= 2;
}
a = (int) ((a * result) % b);
for (int i = 0; i < 3; i++) {
System.out.print(a * 10 / b);
a = (a * 10) % b;
}
}
}
题目描述
运行限制
package 简单数论;
import java.math.BigInteger;
public class 棋盘放麦子 {
public static void main(String[] args) {
BigInteger sum=new BigInteger("1");
BigInteger b=new BigInteger("1");
BigInteger c=new BigInteger("2");
for(int i=2;i<=64;i++) {
b=b.multiply(c);
sum=sum.add(b);
}
System.out.println(sum);
}
}
等差数列:
题目描述
输入描述
输出描述
输入输出样例
5
2 6 4 10 20
10
运行限制
package 简单数论;
import java.util.Arrays;
import java.util.Scanner;
public class 等差数列{
public static int gbc(int a,int b) {
if(b==0) {
return a;
}else {
return gbc(b,a%b);
}
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n=scan.nextInt();
int[] a=new int[n];
for(int i=0;i数数(质因数分解定理)
问题描述
答案提交
运行限制
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
// public static int f(long x) {
// int sum=0;
// for(long i=2;i<=Math.sqrt(x);i++) {
// //找所有的质因数,质因数分解定理
// while(x%i==0) {
// x/=i;
// sum++;
// }
// }
// if(x>1) {
// sum++;
// }
// return sum;
}
public static void main(String[] args) {
// int ans=0;
// for(long i=2333333;i<=23333333;i++) {
// if(f(i)==12) {
// ans++;
// }
// }
System.out.println("25606");
}
}题目描述
运行限制
package 简单数论;
public class 约数个数 {
public static void main(String[] args) {
// TODO Auto-generated method stub
int sum=0,n=1200000;
for(int i=1;i<=Math.sqrt(n);i++) {
if(n%i==0) {
sum+=2;
}
}
System.out.println(sum);
}
}
题目描述
运行限制
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
int sum=0;
for(int i=12;i<=2020;i+=12){
sum++;
}
System.out.println(sum);
}
}题目描述
运行限制
public class 阶乘约数 {
public static void main(String[] args) {
long[] b=new long[101];
for(int i=1;i<=100;i++) {
int x=i;
for(int j=2;j*j<=x;j++) { //质因子分解
if(x%j==0) {
while(x%j==0) {
x/=j;
b[j]++;
}
}
}
if(x>1) {
b[x]++;
}
}
long ans=1;
for(int i=1;i<=100;i++){
if(b[i]!=0) {
ans*=(b[i]+1); //从0开始到,所以要加1
}
}
System.out.println(ans);
}
}
题目描述
运行限制
package 简单数论;
import java.util.Arrays;
public class 合数个数 {
public static void main(String[] args) {
boolean[] a=new boolean[2021];
Arrays.fill(a,true);
for(int i=2;i*i<=2020;i++) {
if(a[i]) {
for(int j=i*i;j<=2020;j+=i) {
a[j]=false;
}
}
}
int sum=0;
for(int i=1;i<=2020;i++) {
if(!a[i]) {
sum++;
}
}
System.out.println(sum);
// int ans=0;
// for(int i=4;i<=2020;i++) {
// boolean flag=false;
// for(int j=2;j*j<=i&&!flag;j++) {
// if(i%j==0) {
// flag=true;
// break;
// }
// }
// if(flag) {
// ans++;
// }
// }
// System.out.println(ans);
}
}
题目描述
输入描述
输出描述
输入输出样例
6
60
运行限制
package 简单数论;
import java.math.BigInteger;
import java.util.Scanner;
public class 最小公倍数 {
public static BigInteger gbc(BigInteger a,BigInteger b) {
if(b==BigInteger.valueOf(0)) {
return a;
}else {
return gbc(b,a.mod(b));
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scan=new Scanner(System.in);
int n=scan.nextInt();
BigInteger sum=BigInteger.valueOf(1);
scan.close();
for(int i=1;i<=n;i++) {
BigInteger s=BigInteger.valueOf(i);
BigInteger d=gbc(sum,s);
sum=sum.multiply(s).divide(d);
}
System.out.println(sum);
}
}
题目描述
运行限制
package 简单数论;
import java.util.Arrays;
public class 找素数 {
public static boolean check(long x) {
for(long i=2;i*i<=x;i++) {
if(x%i==0) {
return false;
}
}
return true;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int sum=0;
for(long i=2;i题目描述
运行限制
注意判断是否为质数的函数的值不要与被模的数相等
public class 纯质数 {
static int[] a= {2,3,5,7};
public static boolean f(int x) {
for(int i=2;i*i<=20210605;i++) {
if(x%i==0&&x!=i) {
return false;
}
}
return true;
}
public static boolean check(int x) { //是质数返回true
for(int i=0;i<4;i++) {
if(a[i]==x) {
return true;
}
}
return false;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
int sum=0;
for(int i=2;i<=20210605;i++) {
boolean flag=true;
int x=i;
while(x>0) {
int a=x%10;
if(!check(a)) {
flag=false;
break;
}
x/=10;
}
if(i==2) {
}
if(flag&&f(i)) {
sum++;
}
}
System.out.print(sum);
}
}
题目描述
运行限制
import java.util.List;
import java.util.Vector;
/**
* @Author zhengwei
* @Date 2021/5/23 3:52 PM
* @Version 1.0
*/
public class _5序列求和 {
static Listimport java.util.Collections;
import java.util.List;
import java.util.Vector;
import static java.lang.Math.min;
import static java.lang.Math.pow;
/**
* @Author zhengwei
* @Date 2021/5/23 3:52 PM
* @Version 1.0
*/
public class _5序列求和2 {
static List题目描述
输入描述
输出描述
输入输出样例
2 4 5
20
运行限制
import java.util.Scanner;
public class 核桃的数量 {
public static int gbc(int a,int b) {
if(b==0) {
return a;
}else {
return gbc(b,a%b);
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scan=new Scanner(System.in);
int[] a=new int[3];
for(int i=0;i<3;i++) {
a[i]=scan.nextInt();
}
scan.close();
int b=1;
b=a[0]*a[1]/gbc(a[0],a[1]);
b=b*a[2]/gbc(b,a[2]);
System.out.print(b);
}
}