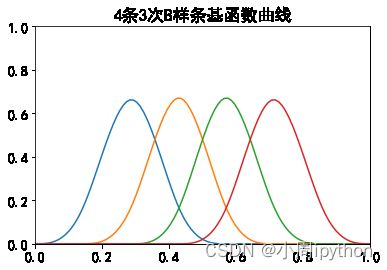
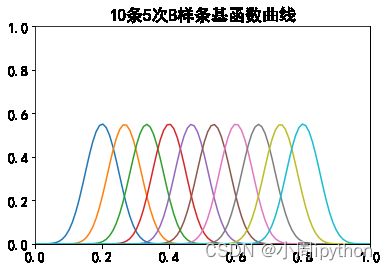
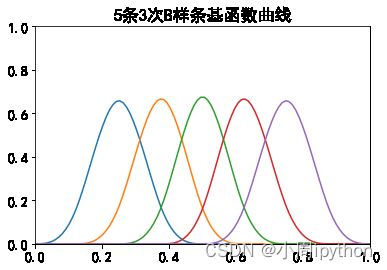
【Python】B样条基函数曲线绘制
1. 原理解释
-
B样条基函数的公式为:
{ N i , 0 ( t ) = { 1 , t ∈ [ t i , t i + 1 ] 0 , 其 他 N i , k ( t ) = t − t i t i + k − t i N i , k − 1 ( t ) + t i + k + 1 − t t i + k + 1 − t i + 1 N i + 1 , k − 1 ( t ) 规 定 0 0 = 0 \left\{ \begin{matrix} N_{i,0}(t)=\left\{ \begin{matrix} 1,\ t\in [t_i,t_{i+1}]\\ 0,\ \ \ \ \ \ \ \ \ \ \ \ 其他 \end{matrix}\right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \\ N_{i,k}(t)=\frac{t-t_i}{t_{i+k}-t_i}N_{i,k-1}(t)+\frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}}N_{i+1,k-1}(t)\\ \\ 规定\frac{0}{0}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{matrix} \right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Ni,0(t)={1, t∈[ti,ti+1]0, 其他 Ni,k(t)=ti+k−tit−tiNi,k−1(t)+ti+k+1−ti+1ti+k+1−tNi+1,k−1(t)规定00=0
-
因此在程序中需要采用递归的方式进行求解。
2. 均匀节点程序
n为B样条曲线的次数
m为基函数曲线的条数
则,节点个数有 n+m+1 个
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
from fractions import Fraction
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
def N(i,k,T,t): # 曲线N_ik
if k == 0:
if t<T[i] or t>T[i+1]:
return 0
else:
return 1
else:
result = (t-T[i])/(T[i+k]-T[i])*N(i,k-1,T,t) + (T[i+k+1]-t)/(T[i+k+1]-T[i+1])*N(i+1,k-1,T,t)
return result
def main(n,m):
T = np.around(np.linspace(0,1,n+m+1),2) # T存储节点
t_x = np.linspace(0,1,100) # t_x存储每一个t值
y = [] # 存储所有曲线的y值
for i in range(m):
list_y = [] # 每次存储一条曲线的y值
for t in t_x:
list_y.append(N(i,n,T,t))
y.append(list_y)
fig = plt.figure()
plt.xlim(0,1)
plt.ylim(0,1)
plt.title('{0}条{1}次B样条基函数曲线'.format(m,n),fontsize=17)
for i in range(m): # 有m条曲线
plt.plot(t_x,y[i])
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
if __name__ == '__main__':
n = int(input('请输入曲线的次数:'))
m = int(input('B样条基函数曲线绘制条数:'))
main(n,m)
3. 结果
4.端点处有重节点原理
- k 次B样条曲线
- V n u m V_{num} Vnum 个控制顶点
- 有 k + V n u m + 1 k+V_{num}+1 k+Vnum+1 个节点, [ 0 , 1 , ⋯ , V n u m , V n u m + 1 , ⋯ , V n u m + k ] [0,1,\cdots,V_{num},V_{num}+1,\cdots,V_{num}+k] [0,1,⋯,Vnum,Vnum+1,⋯,Vnum+k]
- 两端取m重节点,节点区间有 k + V n u m − 2 ( m − 1 ) k+V_{num}-2(m-1) k+Vnum−2(m−1),在线段上的节点应该是 k + V n u m + 1 − 2 m + 2 k+V_{num}+1-2m+2 k+Vnum+1−2m+2
- 基函数个数 V n u m V_{num} Vnum
所以在准均匀B样条基函数绘制中,函数输入应该包含函数次数k,B样条曲线控制顶点数V_num,节点两端的重节点情况m,基函数曲线个数为B_base_num,B_base_num=V_num
5. 端点处有重节点程序
def N(i,k,T,t): # 曲线N_ik
if k == 0:
if t<T[i] or t>T[i+1]:
return 0
else:
return 1
else:
if T[i+k]-T[i] == 0 and T[i+k+1]-T[i+1] == 0:
return 0
elif T[i+k+1]-T[i+1] == 0:
result = (t-T[i])/(T[i+k]-T[i])*N(i,k-1,T,t)
elif T[i+k]-T[i] == 0:
result = (T[i+k+1]-t)/(T[i+k+1]-T[i+1])*N(i+1,k-1,T,t)
else:
result = (t-T[i])/(T[i+k]-T[i])*N(i,k-1,T,t) + (T[i+k+1]-t)/(T[i+k+1]-T[i+1])*N(i+1,k-1,T,t)
return result
# 含有重节点的B样条基函数曲线
def B_basefunc_dup(k,V_num,m,B_base_num):
M0 = np.repeat(0.0,m-1).tolist() # Mi 用来存储两端的重节点
M1 = np.repeat(1.0,m-1).tolist()
T = np.linspace(0,1,V_num+k-2*m+3).tolist() # T 存储在线段上的节点
T_all = M0+T+M1 # T_all 存储全部节点
t_x = np.linspace(0,1,900) # t_x存储每一个t值
y = [] # 存储所有曲线的y值
for i in range(B_base_num):
list_y = [] # 每次存储一条曲线的y值
for t in t_x:
list_y.append(N(i,k,T_all,t))
y.append(list_y)
fig = plt.figure()
# plt.xlim(0,1)
# plt.ylim(0,1)
plt.title('{0}重节点的{1}次B样条基函数曲线'.format(m,k),fontsize=17)
for i in range(B_base_num): # 有m条曲线
# print(y[i],'\n')
plt.plot(t_x,y[i])
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
if __name__ == '__main__':
k = int(input('请输入曲线的次数:'))
V_num = int(input('请输入控制顶点数:'))
m = int(input('请输入端点重节点数:'))
if m == 0:
print('\n重节点数需大于等于1,请重新运行程序!')
else:
B_base_num = V_num # m为基函数曲线数
B_basefunc_dup(k,V_num,m,B_base_num)
# np.linspace(0,1,k+V_num+1-2m+2)