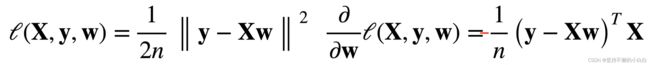《动手学深度学习》（2）线性回归

线性回归

线性模型

线性模型可以看做是单层神经网络
神经网络源于神经科学

衡量线性模型的预估值

平方损失: $l(y,\hat{y})=\frac{1}{2}(y-\hat{y}{)}^2$，其中$y$是真实值， $\hat{y}$是估计值

注：乘$\frac{1}{2}$的目的是求平方的导数的时候，可以消除2

训练数据

收集一些数据点来决定权重和偏差的值，这些数据点就是训练数据，通常越多越好。

训练损失

目标：找到w , $b$，使得训练损失的值最小：

显示解

（这里求导是有一个负号的，但是最终结果不变）

小结

1. 线性回归是对$n$维输入的加权，外加偏差
2. 使用平方损失来衡量预测值和真实值的差异
3. 线性回归有显示解（下面讲的其他模型都没有显示解，因为机器学习用来解决的是NP complete问题）
4. 线性回归可以看作是单层神经网络（最简单的一种神经网络）

基础优化方法

梯度下降法

当模型没有显示解的时候可以用梯度下降求解

梯度下降方法的步骤：

• 挑选一个初始值${\mathbf{w}}_0$;

• 重复迭代参数$t=1,2,3$（如下图）:
  $${\mathbf{w}}_t={\mathbf{w}}_{t-1}-\eta \frac{\partial l}{\partial {\mathbf{w}}_{t-1}}$$

  • 沿梯度方向将增加损失函数
  • 学习率$\eta$：步长的超参数（人为指定，学习率的选择：不能太小（太小找解的速度太慢）也不能太大（太大会发生震荡））

小批量随机梯度下降

实际中很少直接使用梯度下降，深度学习中最常见的梯度求解版本：小批量随机梯度下降

原因：在整个训练集上算梯度太贵了（一个深度神经网络模型可能需要数分钟甚至数小时）。
所以，随机采样$b$个样本$i_1,i_2,\dots ,i_b$来近似损失:
$$\frac{1}{b}\sum _{i\in I_b}l({\mathbf{x}}_i,y_i,\mathbf{w})$$
其中，$b$是批量大小，是另一个重要的超参数（很大时，近似很精确；很小时，近似不是那么精确，但是计算很容易）

• $b$不能太小：每次计算量太小，不适合并行来最大利用计算资源
• $b$不能太大：内存消耗增加，浪费计算资源（例如如果所有样本都是相同的，此时不管多大的批量梯度计算结果都是相同的）

小结

1. 梯度下降通过不断沿着反（负）梯度方向更新参数求解
2. 小批量随机梯度下降是深度学习默认的求解算法
3. 两个重要的超参数：批量大小和学习率

线性回归从0实现

跟着李沐老师视频，总结了里面不理解的一些知识点：

1. “%matplotlib inlines”：是一个魔法函数，可以在Ipython编译器里直接使用，功能是可以内嵌绘图，并且可以省略掉plt.show()这一步[1]。
2. .detach().numpy()：在PyTorch的一些版本里面，需要将数据从计算图中detach出来，才能再转到numpy中去。
3. random.shuffle：随机打乱一组数据，且shuffle只能作用于list，不能作用于tensor类型的数据。
4. yield：python的一个iterate函数，返回一个可以用来迭代（for循环）的生成器
5. with torch.no_grad()：更新的时候不用参与梯度计算的部分
6. .grad：梯度存储的位置；.grad.zeros_()：将梯度设置为0，这样下一次求得的梯度就与上一次无关（因为pytorch会不断的累加变量的梯度，所以每更新一次参数就要让其对应的梯度清零）
7. number of epoch: 数据重复使用的次数，即整个数据“扫描”的次数
8. nan：not a number

线性回归简洁实现

同样跟着李沐老师视频，总结了里面不理解的一些知识点：

1. DataLoader：每次从数据中挑选一定数量的样本，shuffle：是否随机打乱顺序
2. iter()：python迭代器，next(iter())：从迭代器中取出一组数据
3. torch 的 nn model中，有大量的定义好的层；nn.Sequential()：list of layers，也就是一个容器，里面存放神经网络的层

Softmax 回归

Softmax是一种分类方法

分类与回归

• 回归估计一个连续值
  • 单连续数值输出
  • 自然区间 $R$
  • 跟真实值的区别作为损失
• 分类预测一个离散类别
  • 通常多个输出（输出个数等于类别个数）
  • 输出 $i$ 是预测为第 $i$ 类的置信度

从回归到多类分类

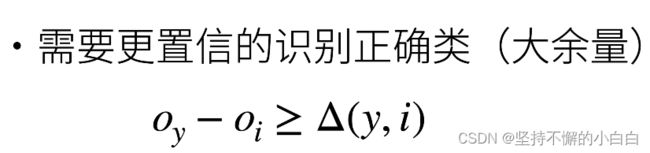
注：$o_y$的值要远大于其他$o_i$的值，这里有一个阈值$\Delta$，至于$o_y$值本身的大小，并不是太关心

注：exp指数函数的好处：不管什么值，都可以变为非负

Softmax和交叉熵损失

注：$y_i$除了真实类别的值为1，其他的都为0，所以可以写为第二个等号后面的内容：真实的类别的预测的值${\hat{y}}_y$的log值取负。
也即对分类问题来讲，不关心对于非正确类的预测值，只关心对于正确类的预测值的置信度要多大。

注：将$l(\mathbf{y},\hat{\mathbf{y}})$展开求导即可得到梯度公式

总结

1. Softmax回归是一个多类分类模型
2. 使用Softmax操作子得到每个类的预测置信度
3. 使用交叉熵来衡量预测和标号的区别

损失函数

1. L2 Loss（均方损失）: $l(y,y^{\prime })=\frac{1}{2}(y-y^{\prime }{)}^2$
   其中，$y$: 真实值, $y^{\prime }$: 预测值
2. L1 Loss：$l(y,y^{\prime })=|y-y^{\prime }|$，预测值与真实值不管间隔多远，梯度永远是常数，即使隔的很远，权重更新也不会特别大，会带来很多稳定性上的好处；缺点：$x=0$点处不可导，此时有一个-1到1的值的变化，在优化末期真实值和预测值差距不那么大时，会变得不那么稳定
3. Huber’s Robust Loss，上述两者的结合
   

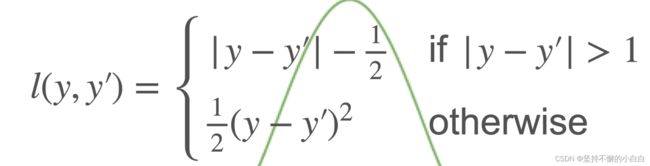
图片分类数据集

数据读取相关的part，跟着李沐老师视频即可。

Softmax回归的实现

从零开始实现和简洁实现视频讲解很清楚，还没有完全理解，后面需要再看一遍

参考
[1] Python绘图问题：Matplotlib中%matplotlib inline是什么、如何使用？
[2] 动手学深度学习PyTorch版B站李沐老师视频列表
[3] 动手学深度学习 (第二版)
[4] Datawhale组队学习