Jacobian and Hessian(雅克比矩阵和海塞矩阵)
雅克比矩阵(Jacobian )
雅可比矩阵 是一阶偏导数以一定方式排列成的矩阵, 其行列式称为雅可比行列式。
假设 F : R n → R m F: R_n \to R_m F:Rn→Rm 是一个从欧式 n 维空间转换到欧式 m 维空间的函数. 这个函数由 m 个实函数组成:,记作

这些函数的偏导数(如果存在)可以组成一个 m 行 n 列的矩阵, 这就是所谓的雅可比矩阵:
[ ∂ y 1 ∂ x 1 ⋯ ∂ y 1 ∂ x n ⋮ ⋱ ⋮ ∂ y m ∂ x 1 ⋯ ∂ y m ∂ x n ] \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} ⎣⎢⎡∂x1∂y1⋮∂x1∂ym⋯⋱⋯∂xn∂y1⋮∂xn∂ym⎦⎥⎤
该矩阵记作 J F ( x 1 , . . . . , x n ) J_F(x_1,....,x_n) JF(x1,....,xn),每一行(一行 n 个数),表示该实数关于 x 的偏导数的集合。
由于矩阵描述了向量空间中的运动——变换,而雅可比矩阵可以看作是将点 x 1 , . . . . , x n x_1,....,x_n x1,....,xn 转化到点 y 1 , . . . . , y n y_1,....,y_n y1,....,yn ,或者说是从一个 n 维的欧式空间转换到 m 维的欧氏空间。
雅克比矩阵的作用:该矩阵的重要性体现在可以利用该矩阵进行线性逼近。
如果 p 是 R n R_n Rn 中的一点,则我们可以根据 F ( p ) F(p) F(p) 所指的向量方向,将 x 逼近与 p,进而获得 F(x) 的表达式为:
F ( x ) ≈ F ( p ) + J F ( p ) ⋅ ( x − p ) F(x)\approx F(p)+J_F(p)\cdot (x-p) F(x)≈F(p)+JF(p)⋅(x−p)
如下图所示,我们可以使用 雅克比矩阵 和 任意点与 p 点的距离 来估算 x 所对应的 f 值(绿色虚线部分)。可以看出,当估计的点距离 p 点越近,估计出来的点的误差越小。这也就是为什么叫做 线性逼近 的原因,也是为什么深度学习时,学习率一般不会很大的原因。
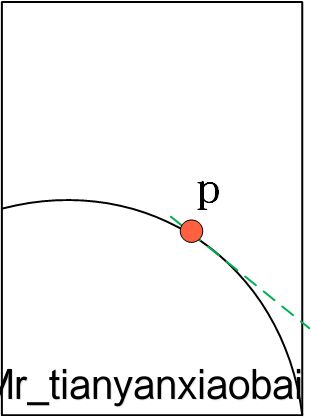
注:可能 PyTorch 和 TensorFlow 中的梯度下降库的实现过程,就是利用了这个 雅克比矩阵。
雅克比行列式
当 m =n 时,雅可比矩阵就是一个方阵,此时他就存在行列式,记作雅克比行列式。
在某个给定点的雅可比行列式提供了 在接近该点时的表现的重要信息.
在二维情况(有直观的图),雅可比行列式代表 xy 平面上的面积微元与 uv 平面上的面积微元的比值。
- 例如, 如果连续可微函数 F 在p 点的雅可比行列式不是零, 那么它在该点附近具有反函数. 这称为反函数定理.
- 更进一步, 如果 p 点的雅可比行列式是正数, 则F FF在p pp点的取向不变;
- 如果是负数, 则 F 的取向相反. 而从雅可比行列式的绝对值, 就可 以知道函数 F在 p 点的缩放因子;
海塞矩阵
在数学中, 海森矩阵(Hessian matrix或Hessian)是 一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵 , 此函数如下:
f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,...,x_n) f(x1,x2,...,xn)
如果 f 的所有二阶导数都存在,那么 f 的海塞矩阵即:
H ( f ) i j ( x ) = D i D j f ( x ) H(f)_{ij}(x)=D_iD_jf(x) H(f)ij(x)=DiDjf(x)
上面的 H ( f ) i j ( x ) H(f)_{ij}(x) H(f)ij(x) 表示 函数关于 第 i 个和第 j 个自变量的二阶偏导,设自变量为 x = ( x 1 , x 2 , x 3 . . . , x n ) x=(x_1,x_2,x_3...,x_n) x=(x1,x2,x3...,xn),即 H(f) 为:
[ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1\,\partial x_n} \\ \\ \frac{\partial^2 f}{\partial x_2\,\partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\,\partial x_n} \\ \\ \vdots & \vdots & \ddots & \vdots \\ \\ \frac{\partial^2 f}{\partial x_n\,\partial x_1} & \frac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤

海森矩阵可以被应用于解决大规模优化问题的牛顿法之中。
海森矩阵的正定与函数凹凸性的关系
Hessian 矩阵的正定性在判断优化算法可行性时非常有用,简单地说,如果函数的二阶偏导数恒大于 0 ,则函数的变化率(斜率)即一阶导数始终处于递增状态,则函数为凸。
因此,在诸如牛顿法等梯度方法中,使用海森矩阵的正定性可以非常便捷的判断函数是否有凸性,也就是是否可收敛到局部/全局的最优解。
若所有特征值均不小于零,则称为半正定。
若所有特征值均大于零,则称为正定。
多元函数Hessian矩阵半正定就相当于一元函数二阶导非负;
多元函数为凸函数的充要条件为其二阶 Hessian 矩阵半正定
海森矩阵的应用
仅仅使用梯度信息的优化算法称之为 一阶优化算法,如梯度下降算法等。
使用 Hessian 矩阵的优化算法称之为 二阶优化算法,如牛顿法等。
一般来说, 牛顿法主要应用在两个方面,
- 1, 求方程的根;
- 2, 最优化;
泰勒公式
求方程的根
其原理便是使用泰勒展开,然后去线性部分,即:
f ( x ) = f ( x 0 ) + ( x − x 0 ) f ′ ( x 0 ) f(x)=f(x_0)+(x-x_0)f'(x_0) f(x)=f(x0)+(x−x0)f′(x0)
然后令上式等于0,则有:
x 1 = x 0 − f ( x 0 ) f ′ ( x 0 ) x_1 = x_0-\frac{f(x_0)}{f'(x_0)} x1=x0−f′(x0)f(x0)
上面式子可以写成如下形式:
x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)
牛顿法求取实根图像步骤如下:
如上图所示,通过梯度(红线的位置)不断更新,直到无限接近 x ∗ x^* x∗ 为止。上图的多变量时,就会引入雅克比矩阵。
最优化
最优化一般是求极大或极小问题,这可以转变为求导数零点,然后转变为 求方程根 的情形。即 f ′ = 0 f' = 0 f′=0;
将 f ( x ) f(x) f(x) 用泰勒公式展开为二阶,如下:
f ( x + d x ) = f ( x ) + f ′ ( x ) d x + 1 2 f ′ ′ ( x ) d x 2 f(x+dx)=f(x)+f'(x)dx+\frac{1}{2}f''(x)dx^2 f(x+dx)=f(x)+f′(x)dx+21f′′(x)dx2
等号左边和 f(x) 近似相等,抵消。然后对 dx 求导得到:
f ′ ( x ) + f ′ ′ ( x ) d x = 0 f'(x)+f''(x)dx=0 f′(x)+f′′(x)dx=0
即:
x n + 1 − x n = d x = − f ′ ( x n ) f ′ ′ ( x n ) x_{n+1}-x_n=dx=-\frac{f'(x_n)}{f''(x_n)} xn+1−xn=dx=−f′′(xn)f′(xn)
即:
x n + 1 = x n − − f ′ ( x n ) f ′ ′ ( x n ) , n = 0 、 1... x_{n+1}=x_n--\frac{f'(x_n)}{f''(x_n)},n=0、1... xn+1=xn−−f′′(xn)f′(xn),n=0、1...
针对于多变量来说,这里的一阶导数就是雅克比矩阵,二阶导数就是海塞矩阵。



