《视觉SLAM十四讲 第二版》笔记及课后习题(第九讲)
读书笔记:后端1
本讲开始,我们转入SLAM 系统的另一个重要模块:后端优化。
我们看到,前端视觉里程计能给出一个短时间内的轨迹和地图,但由于不可避免的误差累积,这个地图在长时间内是不准确的。所以,在视觉里程计的基础上,我们还希望构建一个尺度、规模更大的优化问题,以考虑长时间内的最优轨迹和地图。不过,考虑到精度与性能的平衡,实际当中存在着许多不同的做法。
滤波器后端
关于卡尔曼滤波讲的非常好的一篇教程。
后端(Backend)
- 从带噪声的数据估计内在状态——状态估计问题
- Estimated the inner state from noisy data
渐进式(Incremental)
- 保持当前状态的估计,在加入新信息时,更新已有的估计(滤波)
- 线性系统+高斯噪声=卡尔曼滤波器
- 非线性系统+高斯噪声+线性近似=扩展卡尔曼
- 非线性系统+非高斯噪声+非参数化=粒子滤波器
- Sliding window filter & multiple state Kalman (MSCKF)
批量式(Batch)
- 给定一定规模的数据,计算该数据下的最优估计(优化)
我们又得到了后验均值的表达。总而言之,上面的两个步骤可以归纳为“预测”(Predict)和“更新”(Update)两个步骤:



EKF优点
- 推导简单清楚,适用各种传感器形式
- 易于做多传感器融合
EKF缺点
- 一阶马尔可夫性过于简单
- 可能会发散(要求数据不能有outlier)
- 线性化误差
- 需要存储所有状态量的均值和方差,平方增长
BA与图优化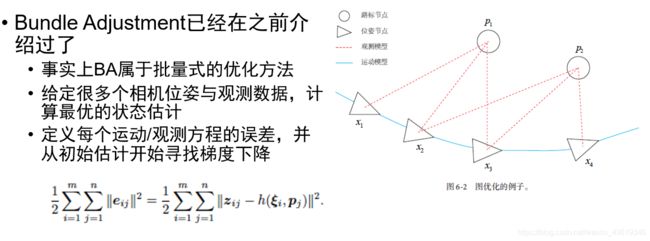


如果对变量做好排序,例如所有相机位姿在前,路标在后,那么 H 有一定的特殊结构。
图模型与H矩阵存在对应关系:图模型中存在边=>H相应地方出现非零块
 H 矩阵中非零矩阵块和图中边的对应关系。如左图当中的H 矩阵当中红色的矩阵块,表示在右图中其对应的变量C2 和P6 之间存在一条边e26。
H 矩阵中非零矩阵块和图中边的对应关系。如左图当中的H 矩阵当中红色的矩阵块,表示在右图中其对应的变量C2 和P6 之间存在一条边e26。
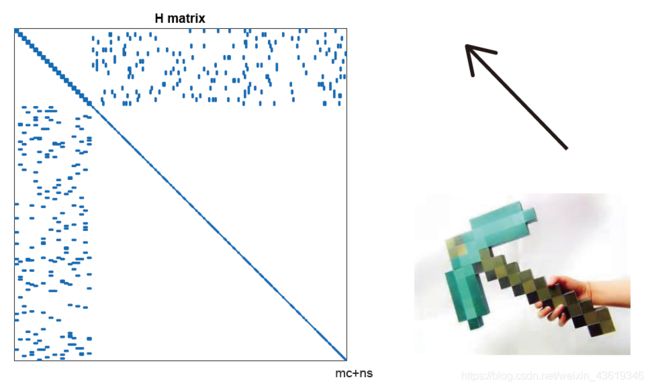
实际当中的H,路标数量远大于位姿数量(箭头形矩阵或镐子形矩阵)




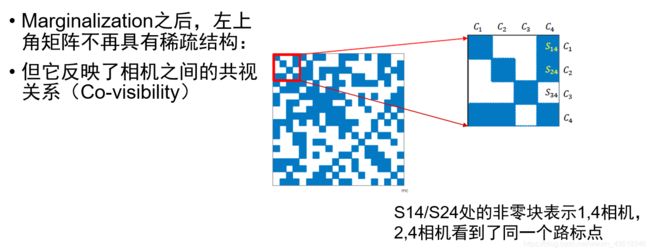

小结:
本讲比较深入地探讨了状态估计问题与图优化的求解。我们看到在经典模型中,SLAM可以看成状态估计问题。如果我们假设马尔可夫性,只考虑当前状态的话,则得到以EKF为代表的滤波器模型。如若不然,我们也可以选择考虑所有的运动和观测,它们构成一个最小二乘问题。在只有观测方程的情况下,这个问题称为BA,并可利用非线性优化方法求解。我们仔细讨论了求解过程中的稀疏性问题,指出了该问题与图优化之间的联系。
实践部分
bundle_adjustment_ceres:
代码运行如下:
/home/wh/shenlan/slambook2/ch9/cmake-build-debug/bundle_adjustment_ceres /home/wh/shenlan/slambook2/ch9/problem-16-22106-pre.txt
Header: 16 22106 83718bal problem file loaded...
bal problem have 16 cameras and 22106 points.
Forming 83718 observations.
Solving ceres BA ...
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.842900e+07 0.00e+00 2.04e+06 0.00e+00 0.00e+00 1.00e+04 0 6.47e-02 2.01e-01
1 1.449093e+06 1.70e+07 1.75e+06 2.16e+03 1.84e+00 3.00e+04 1 1.40e-01 3.41e-01
2 5.848543e+04 1.39e+06 1.30e+06 1.55e+03 1.87e+00 9.00e+04 1 1.30e-01 4.71e-01
3 1.581483e+04 4.27e+04 4.98e+05 4.98e+02 1.29e+00 2.70e+05 1 1.27e-01 5.98e-01
4 1.251823e+04 3.30e+03 4.64e+04 9.96e+01 1.11e+00 8.10e+05 1 1.24e-01 7.23e-01
5 1.240936e+04 1.09e+02 9.78e+03 1.33e+01 1.42e+00 2.43e+06 1 1.23e-01 8.46e-01
6 1.237699e+04 3.24e+01 3.91e+03 5.04e+00 1.70e+00 7.29e+06 1 1.26e-01 9.72e-01
7 1.236187e+04 1.51e+01 1.96e+03 3.40e+00 1.75e+00 2.19e+07 1 1.26e-01 1.10e+00
8 1.235405e+04 7.82e+00 1.03e+03 2.40e+00 1.76e+00 6.56e+07 1 1.25e-01 1.22e+00
9 1.234934e+04 4.71e+00 5.04e+02 1.67e+00 1.87e+00 1.97e+08 1 1.25e-01 1.35e+00
10 1.234610e+04 3.24e+00 4.31e+02 1.15e+00 1.88e+00 5.90e+08 1 1.24e-01 1.47e+00
11 1.234386e+04 2.24e+00 3.27e+02 8.44e-01 1.90e+00 1.77e+09 1 1.26e-01 1.60e+00
12 1.234232e+04 1.54e+00 3.44e+02 6.69e-01 1.82e+00 5.31e+09 1 1.26e-01 1.72e+00
13 1.234126e+04 1.07e+00 2.21e+02 5.45e-01 1.91e+00 1.59e+10 1 1.24e-01 1.85e+00
14 1.234047e+04 7.90e-01 1.12e+02 4.84e-01 1.87e+00 4.78e+10 1 1.26e-01 1.97e+00
15 1.233986e+04 6.07e-01 1.02e+02 4.22e-01 1.95e+00 1.43e+11 1 1.26e-01 2.10e+00
16 1.233934e+04 5.22e-01 1.03e+02 3.82e-01 1.97e+00 4.30e+11 1 1.26e-01 2.23e+00
17 1.233891e+04 4.25e-01 1.07e+02 3.46e-01 1.93e+00 1.29e+12 1 1.24e-01 2.35e+00
18 1.233855e+04 3.59e-01 1.04e+02 3.15e-01 1.96e+00 3.87e+12 1 1.23e-01 2.47e+00
19 1.233825e+04 3.06e-01 9.27e+01 2.88e-01 1.98e+00 1.16e+13 1 1.24e-01 2.60e+00
20 1.233799e+04 2.61e-01 1.17e+02 2.16e-01 1.97e+00 3.49e+13 1 1.24e-01 2.72e+00
21 1.233777e+04 2.18e-01 1.22e+02 1.15e-01 1.97e+00 1.05e+14 1 1.23e-01 2.85e+00
22 1.233760e+04 1.73e-01 1.10e+02 9.19e-02 1.89e+00 3.14e+14 1 1.23e-01 2.97e+00
...
使用 Meshlab 分别打开 g2o 执行文件夹下的 initial.ply 和 final.ply 两个文件,优化前后的效果如下:


bundle_adjustment_g2o :
运行结果如下:
/home/wh/shenlan/slambook2/ch9/cmake-build-debug/bundle_adjustment_g2o /home/wh/shenlan/slambook2/ch9/problem-16-22106-pre.txt
Header: 16 22106 83718iteration= 0 chi2= 8894422.962194 time= 0.265725 cumTime= 0.265725 edges= 83718 schur= 1 lambda= 227.832660 levenbergIter= 1
iteration= 1 chi2= 1772145.543625 time= 0.234101 cumTime= 0.499826 edges= 83718 schur= 1 lambda= 75.944220 levenbergIter= 1
iteration= 2 chi2= 752585.321418 time= 0.232891 cumTime= 0.732716 edges= 83718 schur= 1 lambda= 25.314740 levenbergIter= 1
iteration= 3 chi2= 402814.285609 time= 0.237176 cumTime= 0.969892 edges= 83718 schur= 1 lambda= 8.438247 levenbergIter= 1
iteration= 4 chi2= 284879.389455 time= 0.235331 cumTime= 1.20522 edges= 83718 schur= 1 lambda= 2.812749 levenbergIter= 1
iteration= 5 chi2= 238356.210033 time= 0.235521 cumTime= 1.44074 edges= 83718 schur= 1 lambda= 0.937583 levenbergIter= 1
iteration= 6 chi2= 193550.729802 time= 0.231906 cumTime= 1.67265 edges= 83718 schur= 1 lambda= 0.312528 levenbergIter= 1
iteration= 7 chi2= 146861.192839 time= 0.232932 cumTime= 1.90558 edges= 83718 schur= 1 lambda= 0.104176 levenbergIter= 1
iteration= 8 chi2= 122873.392728 time= 0.231028 cumTime= 2.13661 edges= 83718 schur= 1 lambda= 0.069451 levenbergIter= 1
iteration= 9 chi2= 97812.478436 time= 0.23297 cumTime= 2.36958 edges= 83718 schur= 1 lambda= 0.046300 levenbergIter= 1
iteration= 10 chi2= 80336.316621 time= 0.233388 cumTime= 2.60297 edges= 83718 schur= 1 lambda= 0.030867 levenbergIter= 1
iteration= 11 chi2= 65654.850651 time= 0.230989 cumTime= 2.83396 edges= 83718 schur= 1 lambda= 0.020578 levenbergIter= 1
iteration= 12 chi2= 55967.141021 time= 0.232761 cumTime= 3.06672 edges= 83718 schur= 1 lambda= 0.013719 levenbergIter= 1
iteration= 13 chi2= 53270.115686 time= 0.230372 cumTime= 3.29709 edges= 83718 schur= 1 lambda= 0.009146 levenbergIter= 1
iteration= 14 chi2= 35981.369897 time= 0.276943 cumTime= 3.57403 edges= 83718 schur= 1 lambda= 0.006097 levenbergIter= 2
iteration= 15 chi2= 32092.173309 time= 0.323072 cumTime= 3.89711 edges= 83718 schur= 1 lambda= 0.016259 levenbergIter= 3
iteration= 16 chi2= 31154.877381 time= 0.276839 cumTime= 4.17394 edges= 83718 schur= 1 lambda= 0.021679 levenbergIter= 2
iteration= 17 chi2= 30773.690800 time= 0.230582 cumTime= 4.40453 edges= 83718 schur= 1 lambda= 0.014453 levenbergIter= 1
iteration= 18 chi2= 29079.971263 time= 0.276201 cumTime= 4.68073 edges= 83718 schur= 1 lambda= 0.012508 levenbergIter= 2
iteration= 19 chi2= 28481.944292 time= 0.279615 cumTime= 4.96034 edges= 83718 schur= 1 lambda= 0.016678 levenbergIter= 2
iteration= 20 chi2= 28439.938323 time= 0.232138 cumTime= 5.19248 edges= 83718 schur= 1 lambda= 0.011118 levenbergIter= 1
iteration= 21 chi2= 27171.835892 time= 0.277235 cumTime= 5.46972 edges= 83718 schur= 1 lambda= 0.011153 levenbergIter= 2
iteration= 22 chi2= 26749.623597 time= 0.277069 cumTime= 5.74678 edges= 83718 schur= 1 lambda= 0.014871 levenbergIter= 2
iteration= 23 chi2= 26674.555645 time= 0.232376 cumTime= 5.97916 edges= 83718 schur= 1 lambda= 0.009914 levenbergIter= 1
iteration= 24 chi2= 26089.998120 time= 0.276264 cumTime= 6.25543 edges= 83718 schur= 1 lambda= 0.010288 levenbergIter= 2
iteration= 25 chi2= 25877.861699 time= 0.277238 cumTime= 6.53266 edges= 83718 schur= 1 lambda= 0.013717 levenbergIter= 2
iteration= 26 chi2= 25834.638622 time= 0.230416 cumTime= 6.76308 edges= 83718 schur= 1 lambda= 0.009145 levenbergIter= 1
iteration= 27 chi2= 25570.298632 time= 0.28266 cumTime= 7.04574 edges= 83718 schur= 1 lambda= 0.011127 levenbergIter= 2
iteration= 28 chi2= 25457.520755 time= 0.277767 cumTime= 7.32351 edges= 83718 schur= 1 lambda= 0.011716 levenbergIter= 2
iteration= 29 chi2= 25380.650160 time= 0.277565 cumTime= 7.60107 edges= 83718 schur= 1 lambda= 0.012090 levenbergIter= 2
iteration= 30 chi2= 25362.215118 time= 0.230122 cumTime= 7.83119 edges= 83718 schur= 1 lambda= 0.008060 levenbergIter= 1
iteration= 31 chi2= 25202.452901 time= 0.278364 cumTime= 8.10956 edges= 83718 schur= 1 lambda= 0.008800 levenbergIter= 2
iteration= 32 chi2= 25122.596797 time= 0.276689 cumTime= 8.38625 edges= 83718 schur= 1 lambda= 0.009613 levenbergIter= 2
iteration= 33 chi2= 25115.107638 time= 0.231352 cumTime= 8.6176 edges= 83718 schur= 1 lambda= 0.006408 levenbergIter= 1
iteration= 34 chi2= 24967.189622 time= 0.278329 cumTime= 8.89593 edges= 83718 schur= 1 lambda= 0.006268 levenbergIter= 2
iteration= 35 chi2= 24910.138884 time= 0.276907 cumTime= 9.17283 edges= 83718 schur= 1 lambda= 0.008358 levenbergIter= 2
iteration= 36 chi2= 24867.273980 time= 0.280146 cumTime= 9.45298 edges= 83718 schur= 1 lambda= 0.006277 levenbergIter= 2
iteration= 37 chi2= 24848.840518 time= 0.276981 cumTime= 9.72996 edges= 83718 schur= 1 lambda= 0.008370 levenbergIter= 2
iteration= 38 chi2= 24847.135479 time= 0.233287 cumTime= 9.96325 edges= 83718 schur= 1 lambda= 0.005580 levenbergIter= 1
iteration= 39 chi2= 24798.075555 time= 0.276943 cumTime= 10.2402 edges= 83718 schur= 1 lambda= 0.007249 levenbergIter= 2
Process finished with exit code 0
课后习题
1. 证明式(10.25)成立。提示:你可能会用到SMW(Sherman-Morrison-Woodbury)公式,参考[76, 6]。
考察卡尔曼增益的理解。预测值与测量值的“加权平均”(高斯斑相乘)上的一个迭代过程。依旧是开篇的那篇博客
2. 对比g2o 和Ceres 的优化后目标函数的数值。指出为什么两者在Meshlab 中效果一样但为何数值却不同。
目标函数投影模型的代价函数? 待更新
3. 给Ceres 当中的部分点云进行Schur 消元,看看结果会有什么区别。
Schur消元后,Ceres运行的时间会得到一定程度的提高。
4. 证明S 矩阵为半正定矩阵。
关于半正定的理解。正定、半正定矩阵的直觉代表一个向量经过它的变化后的向量与其本身的夹角小于等于90度。
5. 阅读[28],看看g2o 对核函数是如何处理的。与Ceres 中的Loss function 有何联系?
g2o参考
6. *在两个示例中,我们优化了相机位姿、以 f , k 1 , k 2 f,k_1,k_2 f,k1,k2为参数的相机内参以及路标点。请考虑使用第五章介绍的完整的相机模型进行优化,即,至少考虑 f x , f y , p 1 , p 2 , k 1 , k 2 f_x,f_y,p_1,p_2,k_1,k_2 fx,fy,p1,p2,k1,k2这些量。修改现在的Ceres 和g2o 程序以完成实验。
待填坑。。。