蓝桥杯备赛（三） 数学与简单DP

蓝桥杯备赛（三） 数学与简单DP

一、数学问题

1.Acwing 1205. 买不到的数目
小明开了一家糖果店。
他别出心裁：把水果糖包成4颗一包和7颗一包的两种。
糖果不能拆包卖。
小朋友来买糖的时候，他就用这两种包装来组合。
当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。
你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。
大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。
输入格式
两个正整数 n,mn,m，表示每种包装中糖的颗数。
输出格式
一个正整数，表示最大不能买到的糖数。
数据范围
2≤n,m≤10002≤n,m≤1000，
保证数据一定有解。
输入样例：
4 7
输出样例：
17
暴力做法（会超时，但可以通过一些数据，便于打表找规律）

#include
#include
using namespace std;
int p,q,n;
bool dfs(int m,int p,int q)
{
    if(m==0) return true;
    if(m>=p&&dfs(m-p,p,q)) return true;
    if(m>=q&&dfs(m-q,p,q)) return true;
    
    return false;
}
int main()
{
    cin>>p>>q;
    for(int i=1;i<=1000;i++)
    {
        
        if(!dfs(i,p,q))
            n=max(n,i);
    }
    cout<<n;
    getchar();getchar();
    return 0;
}

这里其实是应用裴蜀定理：
如果 a,b均是正整数且互质，那么由 ax+by, x≥0,y≥0 不能凑出的最大数是 (a−1)(b−1)−1。
若知道此定理，则此题就很简单了

#include
#include
using namespace std;
int main()
{
    int p,q;
    cin>>p>>q;
    cout<<(p-1)*(q-1)-1;
    getchar();getchar();
    return 0;
}

2.Acwing 1211. 蚂蚁感冒
长 100100 厘米的细长直杆子上有 nn 只蚂蚁。
它们的头有的朝左，有的朝右。
每只蚂蚁都只能沿着杆子向前爬，速度是 11 厘米/秒。
当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。
这些蚂蚁中，有 11 只蚂蚁感冒了。
并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。
请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。
输入格式
第一行输入一个整数 nn, 表示蚂蚁的总数。
接着的一行是 nn 个用空格分开的整数 XiXi, XiXi 的绝对值表示蚂蚁离开杆子左边端点的距离。
正值表示头朝右，负值表示头朝左，数据中不会出现 00 值，也不会出现两只蚂蚁占用同一位置。
其中，第一个数据代表的蚂蚁感冒了。
输出格式
输出1个整数，表示最后感冒蚂蚁的数目。
数据范围
1 0<|Xi|<1000<|Xi|<100
输入样例1：
3
5 -2 8
输出样例1：
1
输入样例2：
5
-10 8 -20 12 25
输出样例2：
3

解析：
第一只蚂蚁不管方向朝哪里，只要它右边的蚂蚁向左走就可能碰撞感染，同样，第一只蚂蚁左边的蚂蚁只要朝右边走也可能被感染，这样就很容易得到ans=right+left+1。这里leftleft表示左边蚂蚁向右走的数量，right表示右边蚂蚁向左走的数量，1是指第一只蚂蚁本身。
还有一种特殊情况，就是当第一只蚂蚁向左走的时候，如果第一只蚂蚁左边没有向右爬行的蚂蚁，由于爬行速度相同，所以不管第一只蚂蚁右边有多少向左爬行的，其右边的蚂蚁永远不可能被感染。同理，当第一只蚂蚁向右走的时候，如果第一只蚂蚁右边没有向左爬行的蚂蚁，其左边也永远不可能感染。

//两只蚂蚁相遇调头其实等价于俩只蚂蚁穿过，这样就简单多了
//以第一只感冒蚂蚁为分界点，分为左边与右边
#include
#include
#include 
using namespace std;

int n;
int x[105];
int main()
{
    cin>>n;
    for(int i=0;i<n;i++) cin>>x[i];
    
    int left=0,right=0;  // 分别表示左边向右走的蚂蚁数量，和右边向左走的蚂蚁数量
    for(int i=0;i<n;i++)
    {
        if(x[i]>0&&abs(x[i])<abs(x[0])) left++;
        if(x[i]<0&&abs(x[i])>abs(x[0])) right++;
    }
    if(x[0]>0&&right==0||x[0]<0&&left==0) cout<<1<<endl;  //特殊情况
    else cout<<left+right+1;
    getchar();getchar();
    return 0;
}

二、简单DP

1.Acwing 2 0-1背包问题

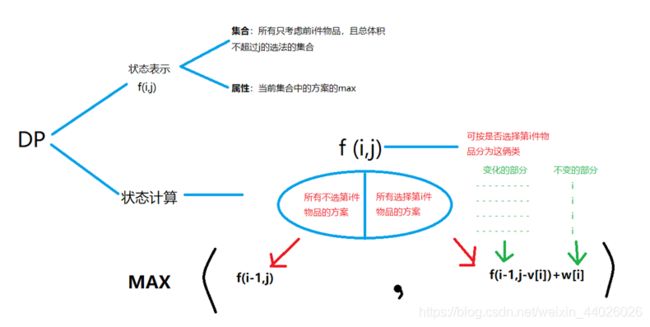
1. 二维动态规划，它的状态转移方程为：
   dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i])

含义：
(1) 如果不装第 ii 件物品，那么问题就转化为“前 i−1i−1 件物品放入容量为 jj 的背包中的最大价值”
(2) 如果装第 ii 件物品，那么问题就转化为“前 i−1i−1 件物品放入剩下的容量为 j−v[i]j−v[i] 的背包中的最大价值”

2. 一维动态规划的状态转移方程（ jj 采取逆序的方式）
   dp[j] = max(dp[j], dp[j - v[i]] + w[i])
   其实两种做法，实现的思想是一样的，只不过一维数组更省空间，下面具体说说，为什么可以用一维数组来代替,而且要采取逆序的方式。
   为何要采取逆序：
   假如枚举到：i = 3, j = 8, v[3] = 5, w[3] = 1
   二维：dp[3][8] = max(dp[2][8], dp[2][3] + w[3]) 此时的dp[2][8]和dp[2][3]都是上一轮的状态值
   一维：dp[8] = max(dp[8], dp[3] + w[3]) 我们要保证dp[8]和dp[3]都是上一轮的状态值

按照逆序的顺序，一维dp数组的更新顺序为：dp[8], dp[7], dp[6], … , dp[3]

也就是说，在本轮更新的值，不会影响本轮中其他未更新的值！较小的index对应的状态是上一轮的状态值！

如果按照顺序进行更新，dp[3] = max(dp[3], dp[0] + w[0])，对dp[3]的状态进行了更新，那么在更新dp[8]时，用到的dp[3]就不是上一轮的状态了，不满足动态规划的要求。
优化后的代码为：

#include
#include
using namespace std;
const int N=1010;
int v[N],w[N]; //体积，价值
int f[N]; //状态转移方程
int n,V;  //n表示物品数量，V表示背包体积
int main()
{
    cin>>n>>V;
    for(int i=1;i<=n;i++)
        cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++) //每一件物品依次枚举
        for(int j=V;j>=v[i];j--) //注意要逆序哦
            f[j]=max(f[j],f[j-v[i]]+w[i]); //状态转移方程
    cout<<f[V];
    getchar();getchar();
    return 0;
}

Acwing 1015
Hello Kitty想摘点花生送给她喜欢的米老鼠。
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。
地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走，不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。

输入格式
第一行是一个整数T，代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式
对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
1≤T≤1001≤T≤100,
1≤R,C≤1001≤R,C≤100,
0≤M≤10000≤M≤1000
输入样例：
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例：
8
16

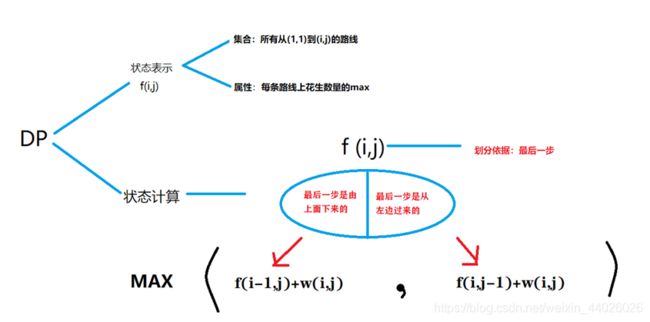
//一道典型的二维DP
//我们需要考虑的是每一步的划分依据，即决策是什么
//每一步的最大值取决于上一步的来源，即上一步是向下还是向右
//最后写出状态转移方程f[i][j]=max(f[i-1][j]+w[i][j],f[i][j-1]+w[i][j])
#include
#include
using namespace std;
const int N=110;
int T,R,C;  
int w[N][N],f[N][N];
int main()
{
    cin>>T;
    while(T--)
    {
        cin>>R>>C;
        for(int i=1;i<=R;i++)
            for(int j=1;j<=C;j++)
                cin>>w[i][j];  
    
    for(int i=1;i<=R;i++)
        for(int j=1;j<=C;j++)
            f[i][j]=max(f[i-1][j]+w[i][j],f[i][j-1]+w[i][j]);
    cout<<f[R][C]<<endl; //最后的那个结果就是我们要找的最大值
    }
    getchar();getchar();
    return 0;
}

Acwing 895. 最长上升子序列
给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。
输入格式
第一行包含整数N。
第二行包含N个整数，表示完整序列。
输出格式
输出一个整数，表示最大长度。
数据范围
1≤N≤10001≤N≤1000，
−109≤数列中的数≤109−109≤数列中的数≤109
输入样例：
7
3 1 2 1 8 5 6
输出样例：
4

#include
#include
#include
#include
using namespace std;
const int N=1001;
int a[N],dp[N]; //dp表示前i个数中的最大上升子序列长度
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
        dp[i]=1;

    for(int i=1;i<=n;i++)
        for(int j=1;j<i;j++)
            if(a[i]>a[j])   
            //若此时第j个数比a[i]要大
            //那么说明前j个数的最大上升子序列加上a[i]构成一个新的最大上升序列
                dp[i]=max(dp[i],dp[j]+1); //
    int res=0;
    for(int i=1;i<n;i++)
        res=max(res,dp[i]);
    cout<<res;
    getchar();getchar();
    return 0;
}

Acwing 1214 波动数列
观察这个数列：
1 3 0 2 -1 1 -2 …
这个数列中后一项总是比前一项增加2或者减少3，且每一项都为整数。
栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加 a或者减少 b 的整数数列可能有多少种呢？
输入格式
共一行，包含四个整数 n,s,a,b含义如前面所述。
输出格式
共一行，包含一个整数，表示满足条件的方案数。
由于这个数很大，请输出方案数除以 100000007的余数。
数据范围
1≤n≤10001≤n≤1000,
−109≤s≤109−109≤s≤109,
1≤a,b≤1061≤a,b≤106
输入样例：
4 10 2 3
输出样例：
2
样例解释
两个满足条件的数列分别是2 4 1 3和7 4 1 -2。

#include
#include
#include
#include
using namespace std;
const int N=1001;
const int MOD=100000007;
int x[N];
int dp[N][N];
int n,s,a,b;
int mod(int x,int n) //保证取模后得到正数
{
    return (x%n+n)%n;
}
int main()
{
    cin>>n>>s>>a>>b;
    dp[0][0] =1 ;//余数不取的话则只能有一个0
    for(int i=1;i<n;i++) //前i项
        for(int j=0;j<n;j++) //余数为j
            dp[i][j]=(dp[i-1][mod(j-(n-i)*a,n)]+dp[i-1][mod(j+(n-i)*b,n)])%MOD;
    cout << dp[n-1][mod(s,n)];
    getchar();getchar();
    return 0;
}