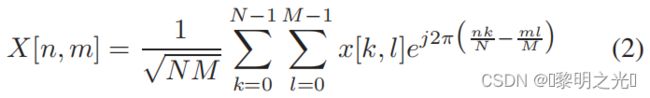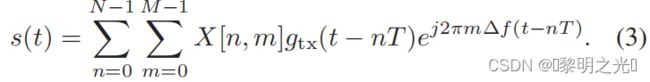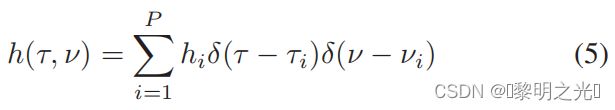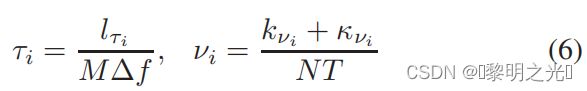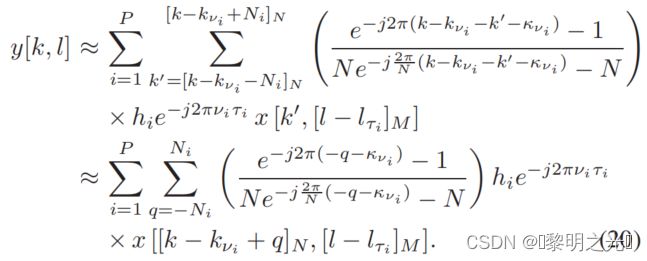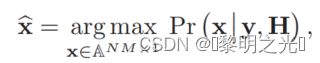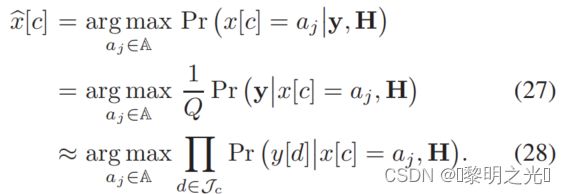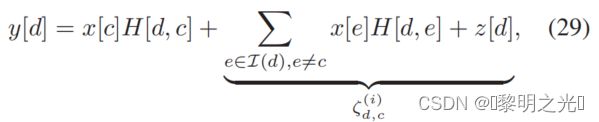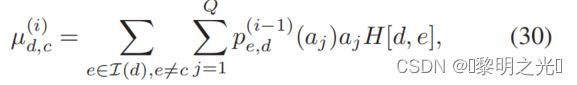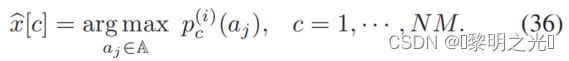OTFS代码学习记录Ⅰ

该代码是Monash University的几位老师开源的（Raviteja Patchava, Yi Hong, and Emanuele Viterbo）首先感谢一下^_^

接下来就开始我们的代码学习过程

首先要解决OTFS发射端和接收端对于输入输出符号调制解调的问题，OTFS发射端的流程图如下图所示：

数据符号x[k,l]

 因此首先就是输入符号x[k,l]的产生，在这里作者使用的是基于格雷码编码的4-QAM调制，如下图所示：

%% random input bits generation and 4QAM modulation%%%%%
        data_info_bit = randi([0,1],N_bits_perfram,1); %生成0或1的随机数，且维数是128*1，也就是生成了一个帧结构中包含的bit数
        data_temp = bi2de(reshape(data_info_bit,N_syms_perfram,M_bits));%二进制数转换成10进制数，reshape为重组数组，语法为reshape(A,a,b)将矩阵A重构为a*b的矩阵
        %reshape(128,64,2)，即将128*1的data_info_bit重组成64*2的矩阵，
        %x = qammod(data_temp,M_mod,0,'gray');
        x = qammod(data_temp,M_mod, 'gray'); %输出使用正交幅度调制4-QAM消息信号X的复包络,gray格雷码编码
        x = reshape(x,N,M); %将64*1的x重组成8*8数组

OTFS调制

然后就是ISSFT变换

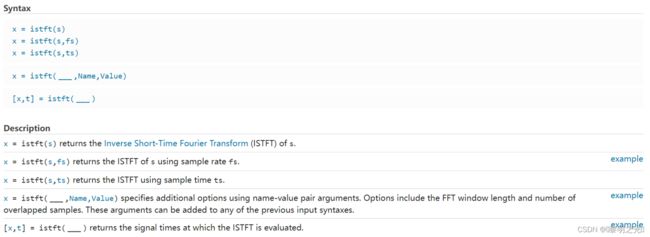
其实matlab官网是有ISFFT和SFFT的函数可以调用的Inverse short-time Fourier transform - MATLAB istft - MathWorks 中国

 作者的实现方式如下：

OTFS发射机首先使用ISFFT将符号X映射到时频网格Λ上的NM样本X[n，m]，如下所示

 对于n = 0，...，N−1，m = 0，...，M−1。

%% OTFS Modulation: 1. ISFFT
X = fft(ifft(x).').'/sqrt(M/N); %%%ISFFT

接下来就是海森堡变换

时频调制器使用发射波形gtx (t)将样本X[n，m]转换为连续的时间波形x(t)

 

 (3)在数学文献中也被称为（离散的）海森堡变换，由参数化的gtx (t)实现

%% OTFS Modulation:2. Heisenberg transform
s_mat = ifft(X.')*sqrt(M); % Heisenberg transform
s = s_mat(:);
end

ISSFT和海森堡拼接在一起就实现了OTFS的调制

function s = OTFS_modulation(N,M,x)
%% OTFS Modulation: 1. ISFFT, 2. Heisenberg transform
X = fft(ifft(x).').'/sqrt(M/N); %%%ISFFT,其中.'表示转置，
s_mat = ifft(X.')*sqrt(M); % Heisenberg transform
s = s_mat(:);%(:)表示将矩阵重构为列向量：
end

 注意：最后生成的s是一个64*1的复数列向量

OTFS解调

 在接收端，一个匹配的滤波器计算交叉模糊度函数Agrx，r（t，f）如下

function y = OTFS_demodulation(N,M,r)
%% OTFS demodulation: 1. Wiegner transform, 2. SFFT
r_mat = reshape(r,M,N);
Y = fft(r_mat)/sqrt(M); % Wigner transform
Y = Y.';
y = ifft(fft(Y).').'/sqrt(N/M); % SFFT
end

调制解调我们解决了之后，就需要考虑在信道中传输和接收端匹配滤波的过程

信道参数生成

需要得到时延和多普勒域中的抽头数量和信道系数，根据文献

”Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation“

可知信号s (t)在具有复基带信道脉冲响应h（τ，ν）的时变信道上传输，它描述了信道对具有延迟τ和多普勒ν 的脉冲的响应。接收信号的r (t)由（忽略噪声以简化符号）表示

由于通常在通道中只有少量的反射器具有相关的延迟和多普勒，因此不需要太多的参数来模拟延迟-多普勒域中的通道。信道h（τ，ν）的稀疏表示为

 P是传播路径的数量；hi、τi和νi分别表示与第i条路径相关的路径增益、延迟和多普勒频移（或频率），δ（·）表示Dirac增量函数。我们表示第i条路径的延迟和多普勒抽头如下

 具体来说，lτi和kνi分别表示（连续）延迟τi抽头系数和多普勒频率νi抽头系数

因此信道参数可以按照下图生成

function [taps,delay_taps,Doppler_taps,chan_coef] = OTFS_channel_gen(N,M)
%% Channel for testing%%%%%
%channel with 4 taps of uniform power%%% 
taps = 4;   %抽头数设置为4
delay_taps = [0 1 2 3]; %时延抽头设置为4
Doppler_taps = [0 1 2 3];   %多普勒域抽头设置为4
pow_prof = (1/taps) * (ones(1,taps));
chan_coef = sqrt(pow_prof).*(sqrt(1/2) * (randn(1,taps)+1i*randn(1,taps)));%信道系数
%%%%%%%%%%%%%%%%%%%%

end

于是按照公式（4）接受信号r（t）可以表示为

function r = OTFS_channel_output(N,M,taps,delay_taps,Doppler_taps,chan_coef,sigma_2,s)
%% wireless channel and noise 
L = max(delay_taps);%最大的时延
s = [s(N*M-L+1:N*M);s];%add one cp %加入循环前缀编码（将OTFS符号数组的后四位信号复制到头部构成的一组（64+4）*1的数组）
s_chan = 0; %信道输入信号初始化
for itao = 1:taps
    s_chan = s_chan+chan_coef(itao)*circshift([s.*exp(1j*2*pi/M *(-L:-L+length(s)-1)*Doppler_taps(itao)/N).';zeros(delay_taps(end),1)],delay_taps(itao));
    %%s_chan是71*1维数组
end
noise = sqrt(sigma_2/2)*(randn(size(s_chan)) + 1i*randn(size(s_chan)));%信道噪声
r = s_chan + noise;
r = r(L+1:L+(N*M));%discard cp(去掉循环前缀，也就是输出68*1维数组的后64位）
end

 经过OTFS解调以及去掉循环前缀后得到的接收函数r为64*1维数组，接下来就要进行联合干扰消除与检测的消息传递算法（MP）

MESSAGE PASSING ALGORITHM

我们现在提出了一种使用（20）（或（24））中的输入-输出关系的OTFS的消息传递（MP）算法。

 A. 低复杂度的MP检测算法

接收到的矢量化信号可以写成

 

 其中y和z是维数NM×1的复向量，元素分别为y[d]和z[d]，1≤d≤NM；H是一个NM×NM复矩阵。x是维数NM×1的信息向量，包含元素x[c]∈A，1≤c≤NM^2,z是噪声。只有当NM中的元素满足如下条件时在H中的元素是非零的。

其中P是传播路径的数量，我们可以看到，由于S比NM小得多，所以H是一个稀疏矩阵（元素大部分为零的矩阵）

请注意，尽管（26）适用于（20）中的理想脉冲情况和（24）中的矩形脉冲情况，但对于不同的矩阵H，这两种情况下H的每一行和列中的非零元素S的数量保持相同。该条件有助于用理想脉冲的复杂度检测算法补偿矩形脉冲的ICI和ISI。

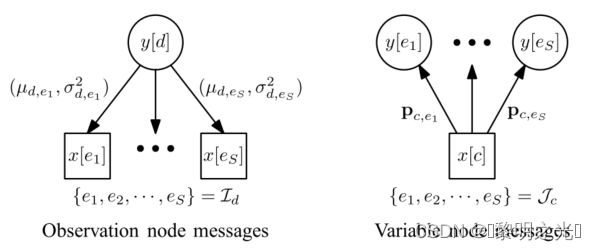
 在（26）的基础上，我们将系统模型为稀疏连接因子图，NM变量节点对应x，NM观测节点对应y。在这个因子图中，每个观测节点y[d]都连接到S个变量节点的集合{x[c]，c∈I (d)}。同样，每个变量节点x[c]连接到S观测节点集{y[d]，d∈J (c)}。如下图所示

从（26）中，给出了估计传输信号的联合最大后验概率（MAP）检测规则

 由于联合MAP检测不利于实际值N和M，我们考虑了c = 1，...，NM的逐符号MAP检测规则

 在（27）中，我们假设所有的传输符号aj∈A都是等可能的，而在（28）中，我们假设y的分量是近似独立的，对于一个给定的x[c]，由于H的稀疏性。为了求解（28）中近似的逐符号MAP检测，我们提出了一种具有线性复杂度的MP检测器。对于每个y[d]，一个变量x[c]与其他干扰项隔离，然后将其近似为高斯噪声，其均值和方差易于计算。

在MP算法中，干扰项的均值和方差被用作从观测节点到变量节点的信息。.另一方面，从一个变量节点x[c]传递到观察节点y[d]d∈J (c)的消息是字母pc的概率质量函数（pmf）d=（aj）|质量函数|aj∈A}。MP算法描述见算法1。

MP算法中迭代i的步骤细节如下

A. 消息从观察节点y[d]传递到变量节点x[c]

干扰的平均μ(i)和方差（σ(i)可似建模为高斯随机变量ζ(i)dc，定义如下

 可以计算为

以及

 B.消息从变量节点x[c]传递到观察节点y[d]

 C.更新决策

如果η(i)>η（i−1），则我们将传输符号的决定更新为

也就是说只有当当前迭代能够提供比上一次迭代更好的估计时，我们才会更新对传输符号的决策

D.停止判据

当至少满足以下条件之一时，MP算法停止。

 我们选择来忽略η的小波动。在这里，第一个条件发生在最好的情况下，其中所有的符号都已经收敛。如果当前迭代提供了比以前迭代中的决策更糟糕的决策，那么第二个条件对于停止算法很有用

值得注意的是，该MP算法也适用于OFDM系统。

先前为OTFS开发的MP也可以用于OFDM符号检测。

由于（38）的形式类似于（26），以前为OTFS开发的MP也可以应用于OFDM符号检测。我们注意到Hofdm在对角线上占优势，当我们远离对角线项时，每一行的非对角线元素的值会在[20]中解释中衰减。因此，Hofdm矩阵也是稀疏的，可以使用所提出的低复杂度MP检测算法。

 

 图中的黄色尖峰即为主对角项，其余幅度较低的是噪声干扰。

仿真结果如下图所示：

 完整代码见主页