模拟退火 | 启发式算法运筹

模拟退火原理
模拟退火解决TSP问题

1.是什么？为什么？怎么做？

• Q1:模拟退火是什么算法？

通过n次迭代，求一个函数的最值

• Q2:模拟退火为什么可行？

模拟退火算法的思想借鉴于固体的退火原理，当固体的温度很高的时候，内能比较大，固体的内部粒子处于快速无序运动，当温度慢慢降低的过程中，固体的内能减小，粒子的慢慢趋于有序，最终，当固体处于常温时，内能达到最小，此时，粒子最为稳定。

注意标粗字体：

温度高->运动速度快（温度低->运动速度慢）
温度是缓慢（想象成特别慢的那种）降低的
温度基本不再变化后，趋于有序(最后内能达到最小，也就是接近最优)
我们通过模拟这个操作，使得我们需要的答案“趋于有序”，也就是最靠近需要的值（最值）。

• Q3:怎么做？

大方向
首先，理解一下大方向：

模拟退火就是一种循环算法。

我们先设定一个初始的温度T
（这个温度会比较高，比如2000）
每次循环都退火一次。（具体怎么操作后面详解）
然后降低T
的温度，我们通过让T
和一个“降温系数”ΔT
（一个接近1的小数，比如0.99)相乘，达到慢慢降低温度的效果，直到接近于0（我们用eps
来代表一个接近0的数(比如0.00001)，只要T 就可以退出循环了）
所以总的来说，用伪代码表示退火的流程是这样的：
流程
首先设定出示的温度T

2、流程

• 1、我们先随机找一点x0 ，

不论是哪个点都可以，随机！（不超过定义域就行）。
这个点作为我们的初始值（相当于物体里的一个粒子）

• 2、再找到一点f(x0),来代表x0所对应的函数值

• 3、现在正式开始退火！

刚才我们说了x0，相当于是一个粒子，所以我们会进行一个无序运动，也就是向左或者向右随机移动
是的，是随机移动，可能向左，也可能向右，但是请记住一个关键点：移动的幅度和当前的温度T
有关。
温度T越大，移动的幅度越大。温度T越小，移动的幅度就越小。这是在模拟粒子无序运动的状态。

• 4、接受(Accept)更"好"的状态

假设我们移动到了x1处，那么这个点对应的f(x1)很明显答案是优于（大于）当前的f(x0)的

因此我们将答案进行更新。也就是将初始值进行替换：x0=x1,f(x0)=f(x1)。这是一种贪心的思想。

• 5、以一定概率接受(Accept)更差的状态

为什么我们要接受一个更加差的状态呢？因为可能在一个较差的状态旁边会出现一个更加高的山峰
如果我们鼠目寸光，只盯着右半区，很容易随着温度的下降、左右跳转幅度的减小而迷失自己，最后困死在小山丘中。
而我们如果找到了左边山峰的低点，以一定的概率接受了它（概率大小和温度以及当前的值的关键程度有关），会在跳转幅度减少之前，尽可能找到最优点。
那么我们以多少的概率去接受它呢？我们用一个公式表示（这个公式我们只需记住，这是科学家推导出来的结论）：

e是自然对数，约等于2.71。我们可以把右上角这一坨值ΔfkT看成一个整体x:
ex的图形画出来是这样的：

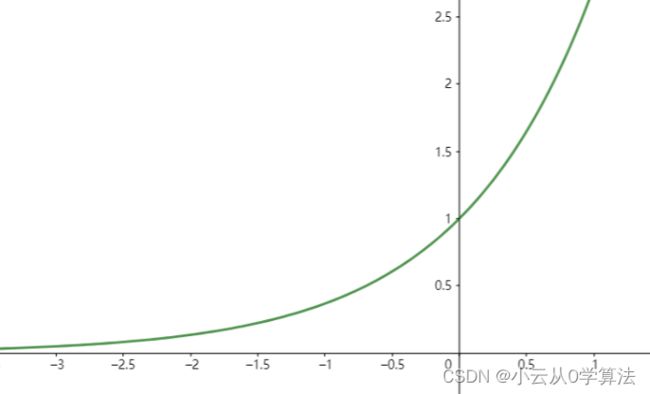
因为我们想要函数ex来代表一个概率值，所以我们只需要关注x为负数的部分即可：
负数部分的值域是在(0,1)开区间内，x越小，越接近0，越大越靠近1。
因为在0到1之间，所以这个值相当于是概率了。比如ex=0.97，那么我们接受的概率就是97%
而正数部分的值域会大于1，也就是说概率会超过100%，所以会一定选（其实是上一种找到更优的情况）

所以总结一下就是：

• 随机后的函数值如果结果更好，我们一定选择它(即x0=x1,f(x0)=f(x1))
• 随机后的函数值如果结果更差，我们以eΔfkT的概率接受它

3、模拟退火优缺点

优点

1、模拟退火算法不需要初始解过好，因此可以用于多种问题。
模拟退火算法的基本思路是从一个随机的解开始，在其周围随机抖动，直到找到最优解或达到一定的终止条件。初始解的好坏只是影响了算法的收敛速度和搜索方向，而并不影响算法的正确性。
2、模拟退火算法可以以一定概率接受更劣的解，从而避免陷入全局最优解的周围，使搜索更全面，更有可能找到真正的最优解。

缺点

① 找到最优解所耗费的时间较长，主要有以下两个原因：

1. 温度降低慢：
   模拟退火算法的核心是温度下降，随着温度的降低，接受劣解的概率逐渐降低，最终趋于0。但是，如果温度降低的过于慢，那么算法将需要更长的时间才能达到较低的温度，也就意味着算法需要更多的迭代次数，时间成本也会增加。

2. 跳出局部最优解缓慢：
   模拟退火算法的另一个核心是可以接受更劣的解，在大部分时间里，接受一个劣解可能是能够跳出局部最优解的唯一方法。但是，当处于局部最优解时，算法可能会被唤醒到其他区域的几率非常小，如果算法陷入了某个较差的局部最优解，它也需要很长时间才能跳出去。
   在温度下降和接受劣解的概率上找到一个合适的权衡，以及在跳出局部最优解上增加多样性和随机性，这些技巧可以加速算法的收敛速度。

4、模拟退火算法求解TSP模型

以下图为例，求从0号城市出发访问每一座城市并回到0号城市的最短回路

模拟退火怎么跳出局部最优解的？
如果当前解是一个局部最优解，即在附近的解中没有比它更好的解，那么一般情况下，该算法仍然会接受这个解，并以一定的概率接受更劣的解，这样就有可能跳出局部最优解并进一步找到全局最优解。

这是因为模拟退火算法维护了一个全局搜索的历史信息，从而可以在全局范围内移动搜索的位置，而不仅限于局部最优解附近的解。在搜索过程中，模拟退火算法会不断改变温度，并决定是否接受更劣的解，从而让搜索过程向全局最优解更有可能靠近。
退火解决TSP问题

模拟退火算法的基本步骤如下：
(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L
(2) 对k=1, …, L做第(3)至第6步：
(3) 产生新解S′
(4) 计算增量ΔT=C(S′)-C(S)，其中C(S)为评价函数
(5) 若ΔT<0则接受S′作为新的当前解，否则以概率exp(-ΔT/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解，结束程序。
(终止条件通常取为连续若干个新解都没有被接受时终止算法。)
(7) T逐渐减少，且T->0，然后转第2步。
#模拟退火算法解TSP问题

import numpy as np
import random as rd
​
def lengthCal(path,distmat):             #计算距离
    length = 0
    for i in range(len(path) - 1):
        length += distmat[path[i]][path[i + 1]]
    length += distmat[path[-1]][path[0]]
    return  length
​
def exchange(path,exchangeSeq):        #交换路径中的两点得到新路径
    newPath = []
    for i in range(len(path)):
        newPath.append(path[i])
    temp = newPath[exchangeSeq[0]]
    newPath[exchangeSeq[0]] = newPath[exchangeSeq[1]]
    newPath[exchangeSeq[1]] = temp
    return newPath
​
distmat = np.array([[0,35,29,67,60,50,66,44,72,41,48,97],
                 [35,0,34,36,28,37,55,49,78,76,70,110],
                 [29,34,0,58,41,63,79,68,103,69,78,130],
                 [67,36,58,0,26,38,61,80,87,110,100,110],
                 [60,28,41,26,0,61,78,73,103,100,96,130],
                 [50,37,63,38,61,0,16,64,50,95,81,95],
                 [66,55,79,61,78,16,0,49,34,82,68,83],
                 [44,49,68,80,73,64,49,0,35,43,30,62],
                 [72,78,103,87,103,50,34,35,0,47,32,48],
                 [41,76,69,110,100,95,82,43,47,0,26,74],
                 [48,70,78,100,96,81,68,30,32,26,0,58],
                 [97,110,130,110,130,95,83,62,48,74,58,0]])
​
T = 100              #初始温度
α = 0.97              #温度变化率
iters = 1000          #每个温度的迭代次数
path= [i for i in range(12)]    #随机初始化路径
rd.shuffle(path)
while T > 10:
    for i in range(iters):
        exchangeSeq = rd.sample(range(0,12),2)
        newPath = exchange(path,exchangeSeq)       #随机交换路径中的两个点
        distanceDif = lengthCal(newPath,distmat) - lengthCal(path,distmat)
        if distanceDif < 0:
            path = newPath                         #接受新的解
        else:
            if rd.random() < np.exp(- distanceDif / T):  #以概率exp(-ΔT/T)接受新的解
                path = newPath
    T = α * T
print("满意解为")
print(path)
print("距离为")
print(lengthCal(path,distmat))

​
模拟退火解决TSP问题案例

https://blog.csdn.net/qq_40894102/article/details/105605228?spm=1001.2014.3001.5502