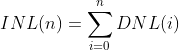ADC技术参数
1、静态参数，STATIC CONVERTER CHARACTERISTICS
1.1、分辨率，Resolution
ADC的分辨率被定义为输入信号值的最小变化，这个最小数值变化会改变数字输出值的一个数值。对于一个理想ADC来说，传递函数是一个步宽等于分辨率的阶梯。然而，在具有较高分辨率的系统中（≥16位），传输函数的响应将相对于理想响应有一个较大的偏离。这是因为ADC以及驱动器电路导致的噪声会降低ADC的分辨率。
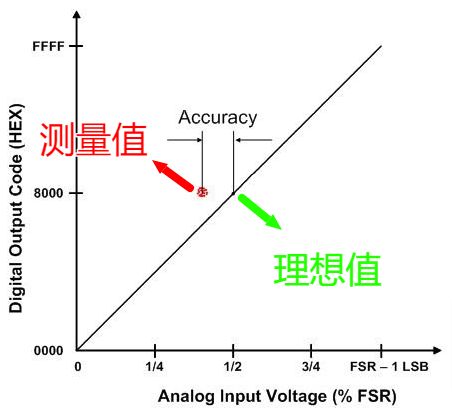
1.1.1、分辨率（Resolution）和精度（Accuracy）的区别
分辨率和精度是两个完全不同的概念。
精度是指对于给定模拟输入，实际数字输出与理论预期数字输出之间的接近度（误差值是多少）。
举个例子，对于只存在Offset=0.1V的12bit FSR=4.096V的ADC来说，分辨率就是12bit（0.001V），而精度就是0.1V。
1.2、DNL，微分非线性，Differential Non Linearity
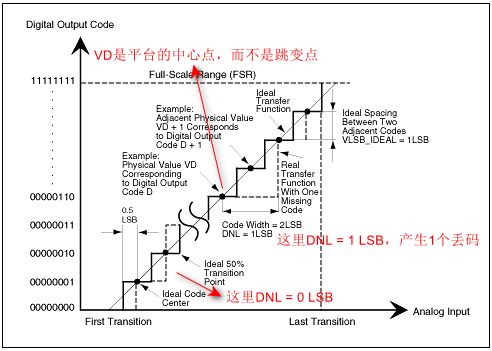
DNL误差定义为实际量化台阶与对应于1 LSB的理想值之间的差异。对于一个理想ADC，其微分非线性为DNL = 0 LSB（
），也就是说每个模拟量化台阶等于1 LSB (1LSB = VFSR/2N，其中VFSR为满量程电压，N是ADC的分辨率)，跳变值之间的间隔为精确的1 LSB。若DNL误差指标≤ 1LSB，就意味着传输函数具有保证的单调性，且没有丢码。当一个ADC的数字量输出随着模拟输入信号的增加而增加时(或保持不变)，就称其具有单调性，相应传输函数曲线的斜率没有变号。DNL指标是在消除了静态增益误差的影响后得到的。具体定义如下：
![DNL = |[(V_{D+1}- V_{D})/V_{LSB-IDEAL} ]- 1 |, 0 < D < 2^{N} - 2](http://img.e-com-net.com/image/info8/ea81d14334be4444b33b785e63f62279.gif){kind=small}
VD是对应于数字输出代码D的输入模拟量，N是ADC分辨率，VLSB-IDEAL是两个相邻代码的理想间隔。较高数值的DNL增加了量化结果中的噪声和寄生成分，限制了ADC的性能，表现为有限的信号-噪声比指标(SNR)和无杂散动态范围指标(SFDR)。
要保证没有丢码（Missing Codes are those output codes that will never appear at the ADC outputs.）和单调的转移函数，ADC的DNL必须小于1 LSB。
1.3、INL，积分非线性，Integral Non Linearity
INL误差表示实际传输函数背离直线的程度，以LSB或满量程的百分比(FSR)来度量。这样，INL误差直接依赖于与之相比较的直线的选取。
至少有两个定义是常用的：“最佳直线INL”和“端点INL” ：
- 最佳直线INL定义中包含了关于失调(截距)和增益(斜率)误差的信息，以及传输函数的位置(在后面讨论)。它定义了一条最接近ADC实际传输函数的直线。没有明确定义直线的精确位置，但这种方法却具有最好的可重复性，能够真正描述器件的线性特征。
- 端点INL所采用的直线经过转换器传输函数的两个端点，因而也就确定了直线的精确位置。这样，对于一个N位ADC来讲，这条直线就由其零点(全0)和其满度(全1)点确定。
最佳直线方法通常被作为首选，因为它能产生比较好的结果。两种INL评估方法是在扣除了静态失调和增益误差后的测量结果，可用下式表示：
![INL = | [(V_{D} - {\color{Red} V_{ZERO})}/V_{LSB-IDEAL}] - {\color{Red} D} |, 0 < D < 2^{N}-1](http://img.e-com-net.com/image/info8/5ce01418f18b404794ad3098c5306d37.gif){kind=small}
或者，
VD是数字输出码D对应的模拟输入，N是ADC的分辨率，VZERO是对应于全零输出码的最低模拟输入，VLSB-IDEAL是两个相邻代码的理想间隔。
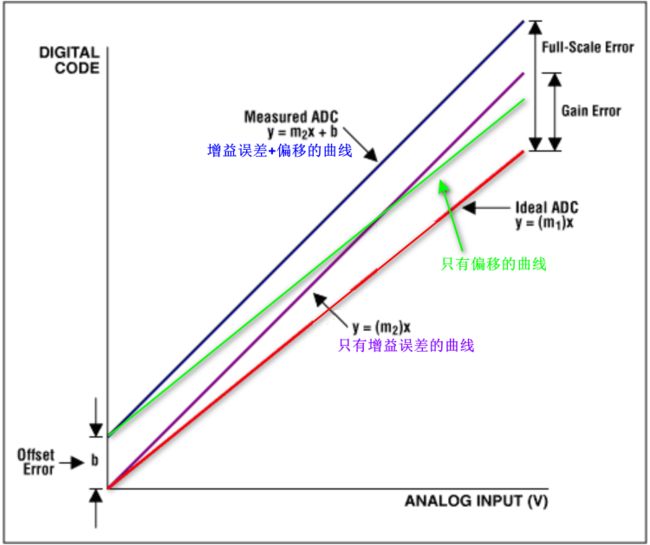
1.4、Offset Error，偏移误差
1.5、Gain Error，增益误差
2、动态参数，DYNAMIC CONVERTER CHARACTERISTICS
2.1、ENOB，有效位数，Effective Number of Bits
ENOB = (SINAD – 1.76)/6.02
2.1.1、有效位数（ENOB）和分辨率（Resolution）的区别
- ENOB一定小于Resolution
- ENOB针对AC信号，分辨率针对DC信号
2.2、SNR，信噪比，Signal-to-Noise Ratio
理论SNR，是仅考虑量化噪声，且无失真情况下的SNR
实际SNR，不仅是量化噪声，还有其他因素影响
2.3、THD，总谐波失真，Total Harmonic Distortion
2.4、SINAD，信纳比，Signal-to-Noise and Distortion Ratio
![SINAD = 10log[P_{S}/(P_{N+D})] = 10logP_{S}-10log(P_{N+D})](http://img.e-com-net.com/image/info8/c323dd27d3344ebeb0503bea249f36f9.gif){kind=small}
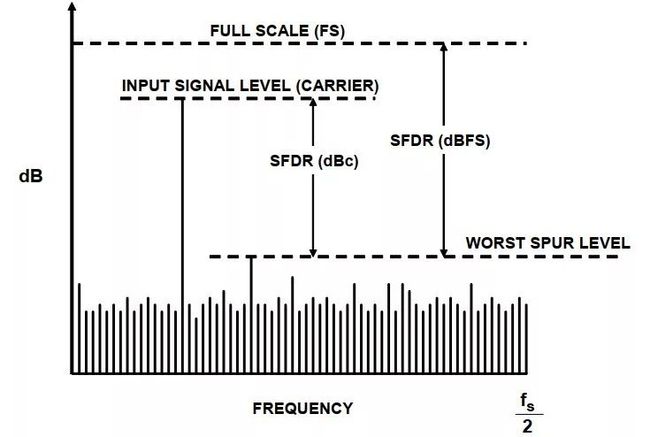
2.5、SFDR，无杂散动态范围，Spurious Free Dynamic Range
2.6、IMD，互调失真，Intermodulation Distortion
2.7、FPBW，全功率带宽，Full Power Bandwidth
2.8、
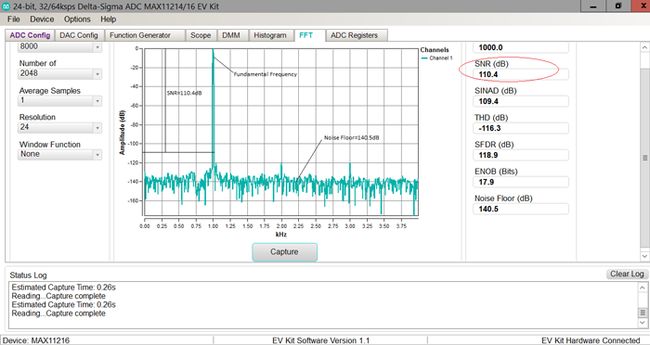
已知（FFT可知）：归一化后，信号功率，PS = 0 dB；噪声功率，PN = -110.4 dB；谐波功率，PD = -116.3 dB；Worst Spur Level = -118.9 dB
可得：
SNR = PS - PN = 110.4 dB
THD = PS - PD = 116.3 dB
SINAD = PS - PN+D = 
SFDR = PS - Worst Spur Level = 118.9 dB
ENOB = (SINAD – 1.76)/6.02 = 17.88 Bits
注意：Noise功率指的是所有noise功率之和，而不是noise floor。
注意：分辨率24 bit的ADC实际SNR才110.4 dB，而理论SNR = 24*6.02+1.76 = 146.24 dB。
3、参数测试
The ABCs of Analog to Digital Converters: How ADC Errors Affect System Performance
Microsoft PowerPoint - Key Parameters.ppt (ti.com)
ADC12020 12-Bit, 20 MSPS, 185 mW A/D Converter with Internal Sample-and-Hold datasheet (Rev. B) (ti.com)