数据结构-链式二叉树

目录

链式二叉树的概念及结构

概念

结构

链式二叉树的遍历

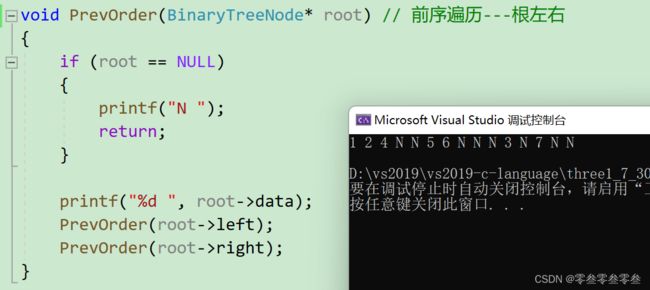
前序遍历

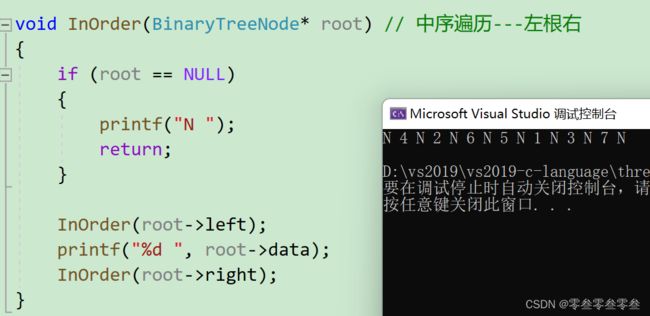
中序遍历

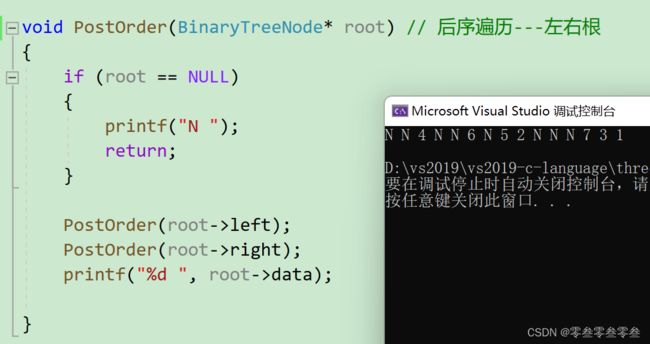
后序遍历

层序遍历

链式二叉树的基本操作

求结点个数BTreeSize

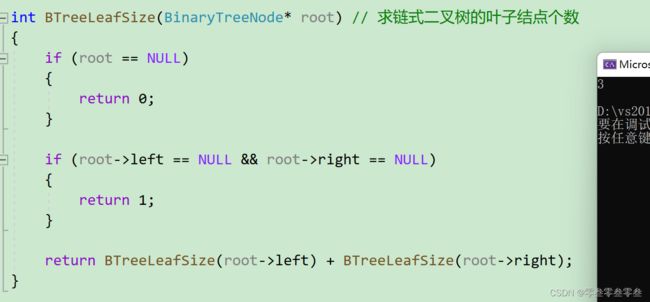
求叶子结点个数BTreeLeafSize

求某一层的结点个数BTreeKLevelSize

求链式二叉树的深度BTreeDepth

判断两棵链式二叉树是否相同BTreeIsSame

链式二叉树的创建与销毁

创建BTreeCreate

销毁BTreeDestroy

代码

---

链式二叉树的概念及结构

概念

   对于那些非完全二叉树，由于顺序存储结构的空间利用率低，因此二叉树一般都采用链式存储结构，用链表结点来存储二叉树中的每一个结点。在链式二叉树中，结点结构通常包括数据域和若干个指针域。

结构

   链式二叉树的结构一般分为两种，一种是二叉链，另一种是三叉链。二叉链的结点包含存储数据的变量，存储左孩子的指针以及存储右孩子的指针。而三叉链的结点除了包含存储数据的变量，存储左孩子的指针以及存储右孩子的指针，还包含存储双亲的指针。特别的在二叉链中，若有n个结点，则一定会有n+1个空指针。

链式二叉树的遍历

   二叉树的遍历是指按某条搜索路径访问树中每个结点，使得每个结点均被访问一次，而且仅被访问一次。因为二叉树是递归定义的，遍历一棵二叉树便要决定对根结点，左子树和右子树的访问顺序。根据访问根结点的顺序不同可以分为前序遍历，中序遍历和后序遍历。以下面这颗二叉树为例：

 

BinaryTreeNode* BuyBinaryTreeNode(BTDataType x) // 创建二叉链结点
{
	BinaryTreeNode* node = (BinaryTreeNode*)malloc(sizeof(BinaryTreeNode));
	if (node == NULL) // 检查结点是否开辟成功
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x; // 先将左右指针置空
	node->left = NULL;
	node->right = NULL;

	return node;
}

int main()
{

    BinaryTreeNode* node1 = BuyBinaryTreeNode(1);
	BinaryTreeNode* node2 = BuyBinaryTreeNode(2);
	BinaryTreeNode* node3 = BuyBinaryTreeNode(3);
	BinaryTreeNode* node4 = BuyBinaryTreeNode(4);
	BinaryTreeNode* node5 = BuyBinaryTreeNode(5);
	BinaryTreeNode* node6 = BuyBinaryTreeNode(6);
	BinaryTreeNode* node7 = BuyBinaryTreeNode(7);
	node1->left = node2;
	node1->right = node3;
	node2->left = node4;
	node2->right = node5;
	node5->left = node6;
	node3->right = node7;

	BinaryTreeNode* root = node1;

}

前序遍历

   先访问根结点，再访问左子树，最后访问右子树。

中序遍历

   先访问左子树，再访问根结点，最后访问右子树。

后序遍历

   先访问左子树，再访问右子树，最后访问根结点。

层序遍历

   进行层序遍历，需要借助队列。先将根结点入队，然后出队，若不为空，则将它的左右结点入队，然后继续入队出队直到队列为空。

// 队列
#include "BinaryTree.h"

typedef struct BinaryTreeNode* QueueDataType; // 存储的数据类型

typedef struct QueueNode
{
	struct QueueNode* next; // 指向下一个结点
	QueueDataType data; // 存储数据
}QueueNode;

typedef struct Queue
{
	QueueNode* head; // 头指针
	QueueNode* tail; // 尾指针
}Queue;

extern void QueueInit(Queue* pq);
extern void QueueDestroy(Queue* pq);
extern void QueuePush(Queue* pq, QueueDataType x);
extern void QueuePop(Queue* pq);
extern QueueDataType QueueFront(Queue* pq);
extern QueueDataType QueueBack(Queue* pq);
extern size_t QueueSize(Queue* pq);
extern bool QueueEmpty(Queue* pq);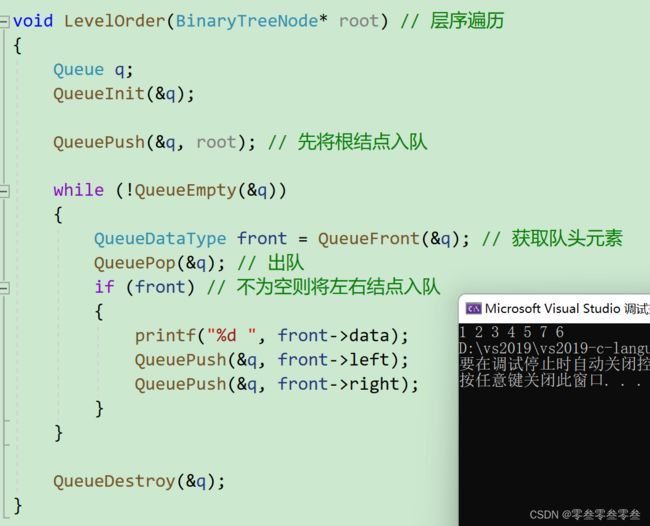

   利用层序遍历可以判断链式二叉树是否为完全二叉树，其思路为：在层序遍历的过程中，如果遇到结点为空则跳出循环，将剩下没有出队的结点依次出队，如果有非空结点出队，则说明该链式二叉树为非完全二叉树；如果剩下没有出队的结点都为空则说明为完全二叉树。

bool BTreeComplete(BinaryTreeNode* root) // 判断是否为完全二叉树
{
	Queue q;
	QueueInit(&q);

	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		QueueDataType front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			/*printf("%d ", front->data);*/
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break; // 遇到空结点跳出循环
		}
	}

	while (!QueueEmpty(&q))
	{
		if (QueueFront(&q)!=NULL) // 遇到非空结点，返回false，说明为非完全二叉树
		{
			QueueDestroy(&q);

			return false;
		}
		QueuePop(&q);
	}

	QueueDestroy(&q);
	return true; // 后面没有非空结点，说明是完全二叉树，返回true
}

链式二叉树的基本操作

求结点个数BTreeSize

求叶子结点个数BTreeLeafSize

求某一层的结点个数BTreeKLevelSize

求链式二叉树的深度BTreeDepth

判断两棵链式二叉树是否相同BTreeIsSame

链式二叉树的创建与销毁

创建BTreeCreate

   创建链接

#include 

typedef struct TreeNode
{
    struct TreeNode* left;
    struct TreeNode* right;
    char ch;
}TreeNode;

TreeNode* TreeCreate(char* p,int* pi)
{
    if(p[*pi]!='\0')
    {    
        if(p[*pi]!='#')
        {
            TreeNode* node=(TreeNode*)malloc(sizeof(TreeNode));
            if(node==NULL)
            {
                perror("malloc");
                return NULL;
            }
            node->ch=p[*pi];
            (*pi)++;
            node->left=TreeCreate(p,pi);
            node->right=TreeCreate(p,pi);
            return node;
        }
        else
        {
            (*pi)++;
            return NULL;
        }
        
    }
    return NULL;
}

void TreeInOrder(TreeNode* root)
{
    if(root==NULL)
        return;
    TreeInOrder(root->left);
    printf("%c ",root->ch);
    TreeInOrder(root->right);
        
}

int main()
{
    char str[101];
    
    scanf("%s",str);
    
    int i=0;
    
    TreeInOrder(TreeCreate(str, &i));
        
    return 0;
}

销毁BTreeDestroy

   链式二叉树的销毁应该采用后序遍历的思想，也就是先销毁左子树，再销毁右子树，最后销毁根节点。避免先销毁根节点，左右子树找不到了。

代码

// 头文件
typedef int BTDataType;

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BinaryTreeNode;



extern BinaryTreeNode* BuyBinaryTreeNode(BTDataType x);
extern void PrevOrder(BinaryTreeNode* root);
extern void InOrder(BinaryTreeNode* root);
extern void PostOrder(BinaryTreeNode* root);
extern int BTreeSize(BinaryTreeNode* root);
extern int BTreeLeafSize(BinaryTreeNode* root);
extern int BTreeKLevelSize(BinaryTreeNode* root, int k);
extern int BTreeDepth(BinaryTreeNode* root);
extern BinaryTreeNode* BTreeFind(BinaryTreeNode* root, BTDataType x);
extern void LevelOrder(BinaryTreeNode* root);
extern bool BTreeComplete(BinaryTreeNode* root);
extern void BTreeDestroy(BinaryTreeNode* root);

// 源文件
void PrevOrder(BinaryTreeNode* root) // 前序遍历---根左右
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

void InOrder(BinaryTreeNode* root) // 中序遍历---左根右
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(BinaryTreeNode* root) // 后序遍历---左右根
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);

}

BinaryTreeNode* BuyBinaryTreeNode(BTDataType x) // 创建二叉链结点
{
	BinaryTreeNode* node = (BinaryTreeNode*)malloc(sizeof(BinaryTreeNode));
	if (node == NULL) // 检查结点是否开辟成功
	{
		perror("malloc fail");
		return NULL;
	}

	node->data = x; // 先将左右指针置空
	node->left = NULL;
	node->right = NULL;

	return node;
}

int BTreeSize(BinaryTreeNode* root) // 求链式二叉树的结点个数
{
	if (root == NULL)
	{
		return 0;
	}

	return 1 + BTreeSize(root->left) + BTreeSize(root->right);
}

int BTreeLeafSize(BinaryTreeNode* root) // 求链式二叉树的叶子结点个数
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

int BTreeKLevelSize(BinaryTreeNode* root, int k) // 求链式二叉树某一层结点的个数 k+3
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}

	return BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1);
}

int BTreeDepth(BinaryTreeNode* root) // 求链式二叉树的层数
{
	if (!root)
	{
		return 0;
	}

	int leftDepth = BTreeDepth(root->left)+1;
	int rightDepth = BTreeDepth(root->right)+1;

	return leftDepth > rightDepth ? leftDepth : rightDepth;
}

BinaryTreeNode* BTreeFind(BinaryTreeNode* root, BTDataType x) // 按值查找
{
	if (!root)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BinaryTreeNode* left = BTreeFind(root->left, x);

	if (left)
		return left;
	BinaryTreeNode* right = BTreeFind(root->right, x);

	if (right)
		return right;

	return NULL;
}

void LevelOrder(BinaryTreeNode* root) // 层序遍历
{
	Queue q;
	QueueInit(&q);

	QueuePush(&q, root); // 先将根结点入队

	while (!QueueEmpty(&q))
	{
		QueueDataType front = QueueFront(&q); // 获取队头元素
		QueuePop(&q); // 出队
		if (front) // 不为空则将左右结点入队
		{
			printf("%d ", front->data);
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	QueueDestroy(&q);
}

bool BTreeComplete(BinaryTreeNode* root) // 判断是否为完全二叉树
{
	Queue q;
	QueueInit(&q);

	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		QueueDataType front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			/*printf("%d ", front->data);*/
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break; // 遇到空结点跳出循环
		}
	}

	while (!QueueEmpty(&q))
	{
		if (QueueFront(&q)!=NULL) // 遇到非空结点，返回false，说明为非完全二叉树
		{
			QueueDestroy(&q);

			return false;
		}
		QueuePop(&q);
	}

	QueueDestroy(&q);
	return true; // 后面没有非空结点，说明是完全二叉树，返回true
}

void BTreeDestroy(BinaryTreeNode* root) // 链式二叉树的销毁
{
	if (!root)
	{
		return;
	}
	BTreeDestroy(root->left);
	BTreeDestroy(root->right);
	free(root);
}

bool isSameTree(BinaryTreeNode* p, BinaryTreeNode* q) // 相同返回true否则返回false
{
	if (p == NULL && q == NULL)
		return true;

	if (p == NULL || q == NULL)
		return false;

	if (p->data != q->data)
		return false;

	return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}