Task 4 CNN简单总结
Task 4 CNN
参考文献：
- https://blog.csdn.net/leviopku/article/details/80327478
- https://datawhalechina.github.io/unusual-deep-learning/#/5.CNN?id=%e5%8d%b7%e7%a7%af%e7%a5%9e%e7%bb%8f%e7%bd%91%e7%bb%9c%e5%9f%ba%e6%9c%ac%e5%8e%9f%e7%90%86
1. 基本概念
卷积神经网络之所以能够有效提取图像特征，是因为图像中物体具有局部不变性特点，其包括：
- 尺度不变性：图像中同一个物体在不同尺度条件下都是同一个物体对象，具有相同特征；
- 平移不变性：图像中同一个物体进行移动操作后具有相同特征；
- 旋转不变性：图像中同一个物体进行旋转操作后具有相同特征。
而基于模板的卷积操作只提取目标对象周围像素值参与计算，不像全连接神经网络每个预测都与所有特征向量直接关系。
卷积：给定一个输入信号序列 x x x和滤波器 w w w，卷积的输出为
y t = ∑ k = 1 K w k x t − k + 1 y_t = \sum_{k = 1}^{K}w_{k}x_{t-k+1} yt=k=1∑Kwkxt−k+1
其中 x t − k + 1 x_{t-k+1} xt−k+1表示在第 k − 1 k-1 k−1个时间步长后的信号值。
采用不同滤波器来提取不同的特征，比如
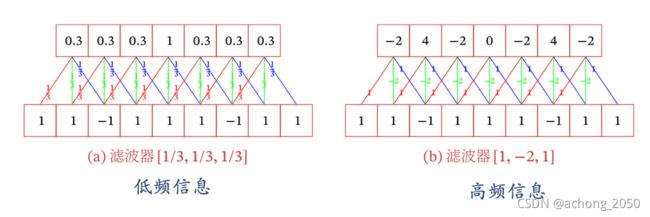
左图展示了能够提取低频信息，当到中间信号向量[1, 1,1]时，因为信号相同变换小，低频时，其输出值最高。滤波器[1/3, 1/3, 1/3]对低频信号敏感，积极响应；
右图展示了能够提取高频信息，信号走到信号向量[1, -1, 1]时，因为信号变换多，高频时，其输出值最高。滤波器[1, -2, 1]对高频信号敏感，积极响应。
一个卷积操作是一个二元运算，有特征图和卷积核，其计算过程是用一个卷积核从左上角开始向右滑动计算每个像素位置的输出值，因为没有进行0填充所以输出特征图小了两个维度，其示意图如下，
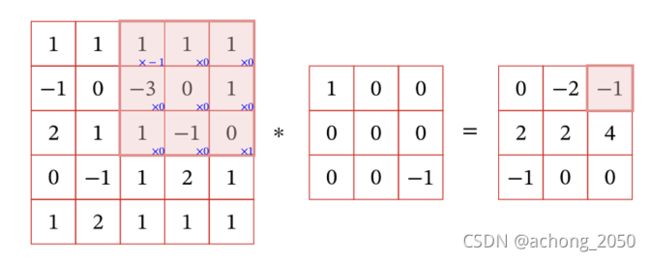
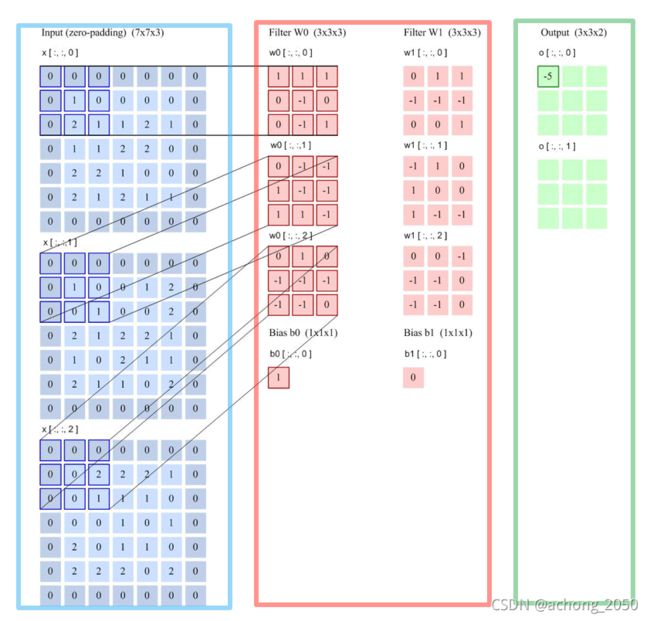
多卷积核的卷积：下图表示卷积核大小为 [ 2 , 3 , 3 , 3 ] ( n u m × c h a n n e l × h i g h × w i d e ) [2, 3, 3, 3] (num \times channel \times high \times wide) [2,3,3,3](num×channel×high×wide)，步长为2，0填充的卷积操作。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HeKUmfKb-1638036191399)(./1638029067347.png)]
其中蓝色框表示被0填充的 [ 7 × 7 × 3 ] [7\times 7 \times 3] [7×7×3]特征向量，红框内表示 [ 3 × 3 × 3 ] [3\times 3\times 3] [3×3×3]卷积核，绿框表示输出一个 [ 3 × 3 × 2 ] [3\times3\times2] [3×3×2]特征向量。
转置卷积从低维特征映射到高维特征
空洞卷积通过给卷积添加空洞，提高空洞率以及卷积核大小，从而提升卷积特征的感受野。
2. 卷积神经网络的基本原理
一般来说，卷积神经网络包括：卷积层、池化层、激活层、全连接层和输出层。
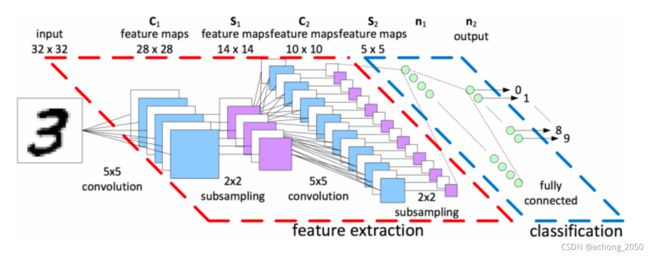
2.1 卷积层
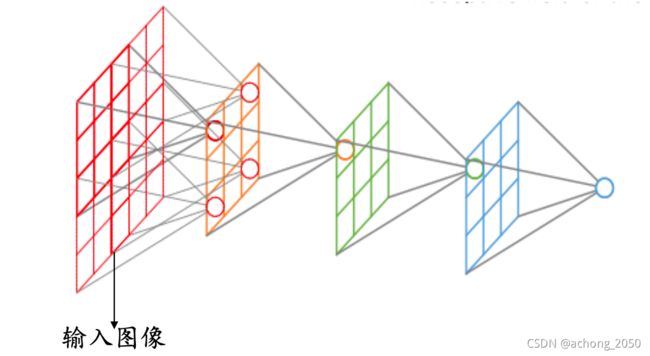
卷积层的计算过程是让卷积核在特征图上以滑动方式遍历每个位置，并计算其特征值，卷积操作如下图所示，
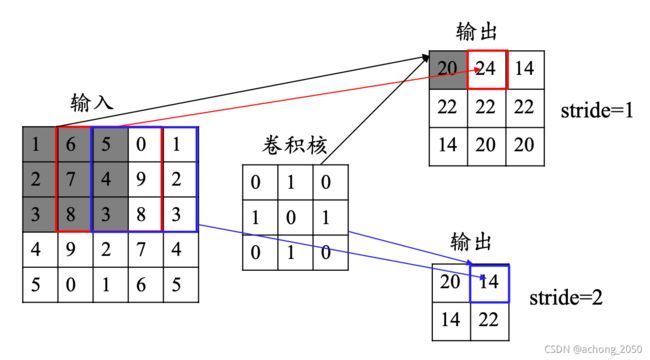
其中步长指的是卷积核移动的格子数目；卷积核的通道数和输入特征图的通道数相同，卷积核的通道不一定如上所示1层，往往是多层的。
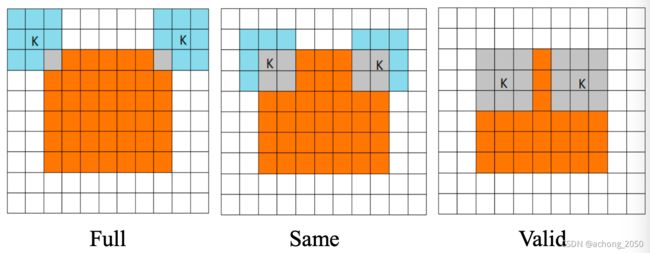
卷积模式对卷积核移动的不同限制，分成full, same, valid mode，其描述如下，
- full mode: 图像和卷积核刚好相交；
- same mode：卷积核中心正好与图像边角相交, 输出与输入具有相同的尺寸；
- valid mode: 卷积核全部都在特征图中。
输出特征的维度：
如果对一个图像 n × n n \times n n×n，采用卷积核 f × f f \times f f×f以步长为1，以0填充 p p p层数据，则输出特征的维度为
感受野：卷积神经网络中特征图中每个像素对输入图像上的区域。
卷积层的深度 也就是卷积层中卷积核的个数。
2.2 池化层
池化层就是使用某个区域的总体统计特征来作为该位置输出，常见的最大池化和平均池化
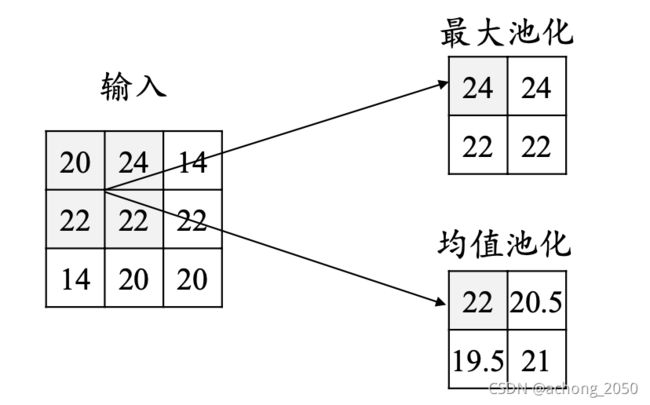
池化层的作用，
- 减少网络参数，遏制过拟合
- 增强网络对小扭曲、平移等噪声的干扰，提高鲁棒性
- 增强网络尺度不变性能力
2.3 激活函数
多层卷积神经网络如果仅是线性函数的叠加，最后其整个模型仍等效于一个线性模型不能提取复杂特征。激活函数用来提高模型非线性，提升特征表征能力。
Relu的特点
其优点为，
- 计算速度快，
- 输入为正数时，不存在梯度消失问题，保证收敛速度
其缺点是， - 武断地将负值置位0，可能丢失一些特征，
- 当输入为负数时，权重无法更新。
2.4 全连接层
所有神经元两两相关联，常用于最后对特征值进行降维，控制输出分类数目。
2.5 输出层
对于分类问题，采用softmax函数将多个分类预测值归一化
y i = e z i ∑ n i = 1 e z i y_i = \frac{e^{z_i}}{\textstyle \sum_{n}^{i=1}e^{z_i}} yi=∑ni=1eziezi
对于回归问题，采用如下公式，
y i = ∑ m = 1 M w i m x m y_i=\sum_{m=1}^{M} w_{im}x_m yi=m=1∑Mwimxm