数据结构之(四):栈
栈初体验之有效的括号
1 、初识栈
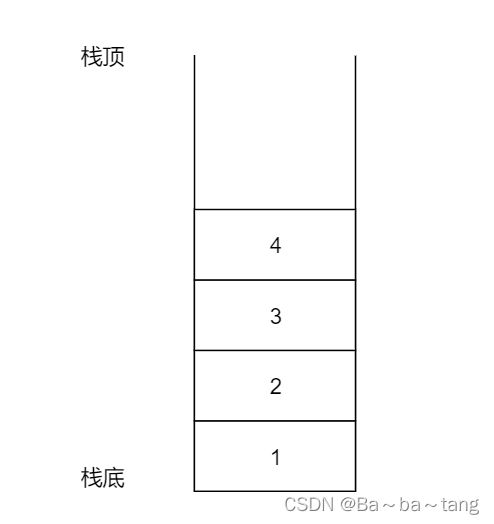
栈 Stack在同一端进行插入和删除 遵循的是先进后出 / 后进先出 LIFO(Last in fifirst out) 的规则存入数据 —— 进栈、压栈 push取出数据 —— 出栈、弹栈 pop比如:浏览器的回退功能 使用的就是栈还有方法调用的过程 也使用了堆栈栈是有记忆的
2 、有效的括号
https://leetcode-cn.com/problems/valid-parentheses/
20. 有效的括号给定一个只包括 '(' , ')' , '{' , '}' , '[' , ']' 的字符串,判断字符串是否有效。有效字符串需满足:左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。注意空字符串可被认为是有效字符串。示例 1:输入 : "()"输出 : true示例 2:输入 : "()[]{}"输出 : true示例 3: 输入 : "(]"输出 : false示例 4:输入 : "([)]"输出 : false示例 5:输入 : "{[]}"输出 : true
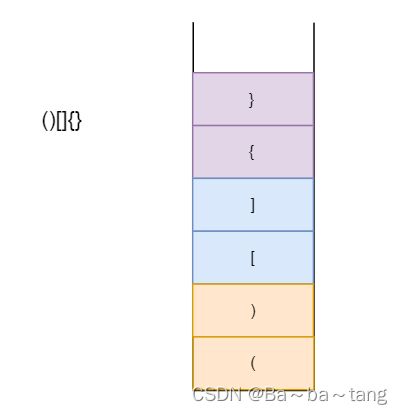
分析 — 通过栈来记录出现的字符方法一:如果是右括号 寻找栈顶元素 能否进行匹配 匹配不上 无效如果是左括号 直接压入栈中当遍历完成的时候 如果不是空栈 说明有左括号未被匹配到 无效是空栈 有效方法二:当出现左括号时 直接存入右括号当出现右括号时 直接取出栈顶元素匹配
public class ValidParenthese {
public static void main(String[] args) {
System.out.println(isValid1("()[]{}"));
System.out.println(isValid1("([)]"));
System.out.println(isValid1("()]"));
System.out.println(isValid1("[()"));
}
//如果是右括号 寻找栈顶元素 能否进行匹配 匹配不上 无效
//如果是左括号 直接压入栈中
// 当遍历完成的时候 如果不是空栈 说明有左括号未被匹配到 无效
// 是空栈 有效
public static boolean isValid(String s) {
// 用映射关系 记录匹配 () [] {}
Map map = new HashMap<>();
map.put('(', ')');
map.put('[', ']');
map.put('{', '}');
Stack stack = new Stack<>();
char[] arr = s.toCharArray();
for (char c : arr) {
if (map.containsKey(c)) {
// 左括号
stack.push(c);
} else {
// 右括号
if (stack.empty()) {
System.out.println("右括号出现 但左括号仍未出现");
return false;
}
// 取出栈顶元素
char top = stack.peek();
if (!map.get(top).equals(c)) {
System.out.println("右括号出现 但不是与之对应的左括号");
return false;
}
// 弹出 左括号 已被抵消
stack.pop();
}
}
if (!stack.empty()) {
System.out.println("左括号出现 但右括号仍未出现");
return false;
}
return true;
}
// 当出现左括号时 直接存入右括号
// 当出现右括号时 直接取出栈顶元素匹配
public static boolean isValid1(String s) {
Stack stack = new Stack<>();
for (char c : s.toCharArray()) {
if (c == '(') {
stack.push(')');
} else if (c == '[') {
stack.push(']');
} else if (c == '{') {
stack.push('}');
} else if (stack.empty() || c != stack.pop()) {
return false;
}
}
return stack.empty();
}
}
栈的多种实现方式
用数组实现栈栈的实现方式:按照存储结构的不同分为,顺序栈和链栈
public class MyStackByArray {
// 存储数据
int[] array;
// 最大容量
int maxSize;
// 实际存储大小
int top;
public MyStackByArray(int size) {
maxSize = size;
array = new int[size];
top = -1;
}
public void push(int value) {
if (top < maxSize - 1) {
top++;
array[top] = value;
}
}
public int pop() {
int result = array[top];
top--;
return result;
}
public int peek() {
return array[top];
}
public boolean isEmpty() {
return top == -1;
}
public boolean isFull() {
return top == (maxSize - 1);
}
public static void main(String[] args) {
MyStackByArray stack = new MyStackByArray(3);
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack.isFull());
System.out.println(stack.peek());
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.isEmpty());
}
} 用队列实现栈
https://leetcode-cn.com/problems/implement-stack-using-queues/
225. 用队列实现栈使用队列实现栈的下列操作:push(x) -- 元素 x 入栈pop() -- 移除栈顶元素top() -- 获取栈顶元素empty() -- 返回栈是否为空注意 :你只能使用队列的基本操作 -- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。你所使用的语言也许不支持队列。 你可以使用 list 或者 deque (双端队列)来模拟一个队列 , 只要是标准的队列操作即可。你可以假设所有操作都是有效的(例如 , 对一个空的栈不会调用 pop 或者 top 操作)。 225. 用队列实现栈使用队列实现栈的下列操作:push(x) -- 元素 x 入栈pop() -- 移除栈顶元素top() -- 获取栈顶元素empty() -- 返回栈是否为空
分析:队列 先进先出 栈 先进后出方法一:额外的队列 作为临时空间 在取数据时 存储队列中其他元素 知道找到队尾元素 操作之后 再将临时队列中的元素移回
public class MyStackByQueue {
// 存储数据的队列
Queue dataQueue = new LinkedList<>();
// 临时队列
Queue tmpQueue = new LinkedList<>();
// 记录栈顶元素
int top;
/**
* Push element x onto stack.
*/
public void push(int x) {
dataQueue.add(x);
top = x;
}
/**
* Removes the element on top of the stack and returns that element.
*/
public int pop() {
while (dataQueue.size() > 1) {
top = dataQueue.poll();
tmpQueue.add(top);
}
int num = dataQueue.poll();
// 再将dataQueue元素移回去
Queue tmp = dataQueue;
dataQueue = tmpQueue;
tmpQueue = tmp;
return num;
}
/**
* Get the top element.
*/
public int top() {
return top;
}
/**
* Returns whether the stack is empty.
*/
public boolean empty() {
return dataQueue.size() == 0;
}
} 方法二:
不使用额外对列 在每次存数据时 颠倒其位置 保存的顺序满足栈的处理顺序
public class MyStackByQueue2 {
Queue queue = new LinkedList<>();
/**
* Push element x onto stack.
*/
public void push(int x) {
queue.add(x);
//把队头元素 拿出来 放到队尾 颠倒 size-1次
int size = queue.size();
while (size > 1) {
int tail = queue.poll();
queue.offer(tail);
size--;
}
}
/**
* Removes the element on top of the stack and returns that element.
*/
public int pop() {
return queue.poll();
}
/**
* Get the top element.
*/
public int top() {
return queue.peek();
}
/**
* Returns whether the stack is empty.
*/
public boolean empty() {
return queue.isEmpty();
}
} 常见面试题之栈的最小值
栈的最小值
https://leetcode-cn.com/problems/min-stack-lcci/
面试题 03.02. 栈的最小值请设计一个栈,除了常规栈支持的 pop 与 push 函数以外,还支持 min 函数,该函数返回栈元素中的最小值。执行 push 、 pop 和 min 操作的时间复杂度必须为 O(1) 。示例:MinStack minStack = new MinStack();minStack.push(-2);minStack.push(0);minStack.push(-3);minStack.getMin(); --> 返回 -3.minStack.pop();minStack.top(); --> 返回 0.minStack.getMin(); --> 返回 -2.
分析:【方式一】尝试用额外的栈 来记录数据栈的最小值dataStack -2 0 -3 1minStack -2 -2 -3 -3dataStack -2 0 -4minStack -2 -2 -4
public class MinStack {
// 数据栈
Stack dataStack = new Stack<>();
// 存储最小值的额外栈
Stack minStack = new Stack<>();
/**
* initialize your data structure here.
*/
public MinStack() {
}
public void push(int x) {
dataStack.push(x);
// 比较新元素 和minStack中栈顶元素(之前所有元素的最小值) 谁更小
if (!minStack.isEmpty() && minStack.peek() < x) {
// 如果栈顶元素更小 再存进栈一次
minStack.push(minStack.peek());
} else {
minStack.push(x);
}
}
public void pop() {
dataStack.pop();
minStack.pop();
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return minStack.peek();
}
} 【方式二】不使用额外的栈 使用变量来标记栈的最小元素核心问题在于 如何记录之前的最小值?[-2 0 -3 1 ]dataStack [-2 0 -2 -3 1]min -2 -> -3dataStack [-2 0]min -2
public class MinStack1 {
Stack dataStack = new Stack<>();
int min = Integer.MAX_VALUE;
public void push(int x) {
// 如果新元素使最小值发生变化 则会存储两个值 (原来的最小值 当前的最小值)
if (min >= x) {
// 如果栈为空 说明是第一个元素 此时一定min>x
if (!dataStack.isEmpty()) {
dataStack.push(min);
}
// 最小值重新赋值
min = x;
}
dataStack.push(x);
}
public void pop() {
if (dataStack.isEmpty()) return;
if (dataStack.size() == 1) {
min = Integer.MAX_VALUE;
} else if (min == dataStack.peek()) {
dataStack.pop();
min = dataStack.peek();
}
// 如果移除的不是最小值 直接pop
// 如果移除的是最小值 前面移除一次 再移除之前保存的最小值
dataStack.pop();
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return min;
}
} 常见面试题之下一个更大元素
下一个更大元素
https://leetcode-cn.com/problems/next-greater-element-i/
496. 下一个更大元素 I给定两个 没有重复元素 的数组 nums1 和 nums2 ,其中 nums1 是 nums2 的子集。找到nums1 中每个元素在 nums2 中的下一个比其大的值。nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。示例 1:输入 : nums1 = [4,1,2], nums2 = [1,3,4,2].输出 : [-1,3,-1]解释 :对于 num1 中的数字 4 ,你无法在第二个数组中找到下一个更大的数字,因此输出 -1 。对于 num1 中的数字 1 ,第二个数组中数字 1 右边的下一个较大数字是 3 。对于 num1 中的数字 2 ,第二个数组中没有下一个更大的数字,因此输出 -1 。
分析:暂时忽略 nums1 直接求取 nums2 中 每个元素的下一个更大值用栈实现arr [2,3,5,1,0,7,4]map <2,3> <3,5> <0,7> <1,7> <5,7> <4,-1> <7,-1>stack [2] -> 3stack [3] -> 5stack [5] -> 1stack [5,1] -> 0stack [5,1,0] -> 7stack [7] -> 4stack [7,4]
public static int[] nextGreaterElement(int[] nums1, int[] nums2) {
//暂时忽略nums1 直接求取nums2中 每个元素的下一个更大值
Stack stack = new Stack<>();
Map map = new HashMap<>();
int[] result = new int[nums1.length];
for (int i = 0; i < nums2.length; i++) {
// 比较 栈顶元素和新元素
while (!stack.empty() && nums2[i] > stack.peek()) {
map.put(stack.pop(), nums2[i]);
}
// 如果新元素更小 直接入栈 等待后面出现的更大元素
// 如果找到更大元素 存入map后 新元素仍要入站
stack.push(nums2[i]);
}
// 如果栈中还有元素 代表没有出现过更大元素
while (!stack.empty()) {
map.put(stack.pop(), -1);
}
for (int i = 0; i < nums1.length; i++) {
result[i] = map.get(nums1[i]);
}
return result;
}
} 经典应用之逆波兰表达式
前缀、中缀、后缀表达式
算术表达式3+4-5 = 23+4*5 = 23数字 运算符前缀、中缀、后缀表达式 (指的是运算符的位置)前缀又叫 波兰表达式后缀又叫 逆波兰表达式3+4-5中缀: 3+4-5前缀: +-543后缀: 34+5-
【逆波兰表达式】
https://leetcode-cn.com/problems/evaluate-reverse-polish-notation/
150. 逆波兰表达式求值根据 逆波兰表示法,求表达式的值。有效的运算符包括 +, -, *, / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。说明:整数除法只保留整数部分。给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。示例 1 :输入 : ["2", "1", "+", "3", "*"]输出 : 9解释 : 该算式转化为常见的中缀算术表达式为: ((2 + 1) * 3) = 9示例 2 :输入 : ["4", "13", "5", "/", "+"]输出 : 6解释 : 该算式转化为常见的中缀算术表达式为: (4 + (13 / 5)) = 6
分析:后缀是自带优先级的表达式["2", "1", "+", "3", "*"] 出现数字 即存入栈中出现运算符 取出栈中的两个数字 进行相应运算 运算结果入栈stack [2,1] -> +stack [3]stack [3,3] -> *stack [9]
public static int evalRPN(String[] tokens) {
Stack stack = new Stack<>();
int num1, num2;
for (int i = 0; i < tokens.length; i++) {
switch (tokens[i]) {
case "+":
num1 = Integer.parseInt(stack.pop());
num2 = Integer.parseInt(stack.pop());
stack.push(num2 + num1 + "");
break;
case "-":
num1 = Integer.parseInt(stack.pop());
num2 = Integer.parseInt(stack.pop());
stack.push(num2 - num1 + "");
break;
case "*":
num1 = Integer.parseInt(stack.pop());
num2 = Integer.parseInt(stack.pop());
stack.push(num2 * num1 + "");
break;
case "/":
num1 = Integer.parseInt(stack.pop());
num2 = Integer.parseInt(stack.pop());
stack.push(num2 / num1 + "");
break;
default:
// 如果是数字 直接入栈
stack.push(tokens[i]);
}
}
return Integer.parseInt(stack.pop());
} 【中缀转后缀】
将中缀表达式转换为后缀表达式1 初始化两个栈:运算符栈 s1 和储存中间结果的栈 s2 ;2 从左至右扫描中缀表达式;遇到操作数时,将其压 s2 ;遇到运算符时,比较其与 s1 栈顶运算符的优先级:如果 s1 为空,或栈顶运算符为左括号 “(” ,则直接将此运算符入栈;否则,若优先级比栈顶运算符的高,也将运算符压入 s1 ;否则,将 s1 栈顶的运算符弹出并压入到 s2 中,再次转到与 s1 中新的栈顶运算符相比较; 遇到括号时:如果是左括号 “(” ,则直接压入 s1 ;如果是右括号 “)” ,则依次弹出 s1 栈顶的运算符,并压入 s2 ,直到遇到左括号为止,此时将这一对括号丢弃;重复以上步骤,直到表达式的最右边;3 将 s1 中剩余的运算符依次弹出并压入 s2 ;4 依次弹出 s2 中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式
1+((2+3)*4)-5
// 中缀转后缀
public static void transfer(String str) {
// 运算符栈
Stack stack1 = new Stack<>();
// 中间结果栈
Stack stack2 = new Stack<>();
char[] chars = str.toCharArray();
for (int i = 0; i < chars.length; i++) {
switch (chars[i]) {
//判断 是运算符 还是 操作数 以及 具体的加减乘除或括号
case '+':
case '-':
case '*':
case '/':
// 有两种情况 直接存入s1
// 如果s1为空 或者 栈顶元素是左括号
// 如果 当前运算符 优先级比栈顶元素高 直接存入
while (true) {
if (stack1.isEmpty() || stack1.peek().equals('(')
|| compare(chars[i], stack1.peek()) > 0) {
stack1.push(chars[i]);
break;
}
stack2.push(stack1.pop());
}
break;
case '(':
stack1.push(chars[i]);
break;
case ')':
// 找到stack1中 左括号的位置
while (!stack1.peek().equals('(')) {
// 中间运算符 取出并存入s2
stack2.push(stack1.pop());
}
// 此时左括号被抵消 所以取出
stack1.pop();
break;
default:
// 是数字
stack2.push(chars[i]);
}
}
while (!stack1.empty()) {
stack2.push(stack1.pop());
}
// 将栈中元素 倒序输出到数组中
String[] arr = new String[stack2.size()];
int size = stack2.size() - 1;
while (!stack2.isEmpty()) {
arr[size] = stack2.pop() + "";
size--;
}
System.out.println(Arrays.toString(arr));
}