K近邻分类算法的Python代码实现

问题描述

K近邻算法解决的是机器学习领域中，监督学习类别下的回归和分类问题。监督学习是指利用数据的特征及其对应的标签来训练模型，然后基于模型预测未知的标签。如果标签是离散值，如比赛结果是输或赢、邮件是否为垃圾邮件，则为分类；如果标签是连续值，如某个地区下半年的GDP，则为回归。
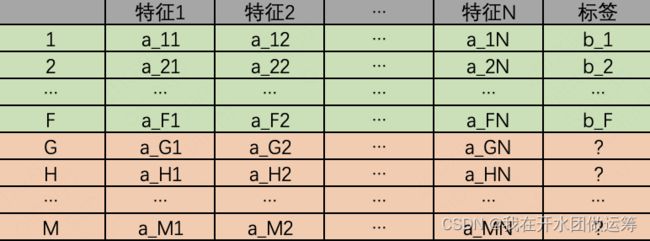
以下图为例。共有0-F条数据，每条数据分别包含N个特征和一个标签。使用K近邻算法后，可以得到一个模型。模型可以视为如下的一个F函数：标签=F(特征1, 特征2, …, 特征N)。得到该模型后，便可以预估得到G~M个数据的标签。

算法方案

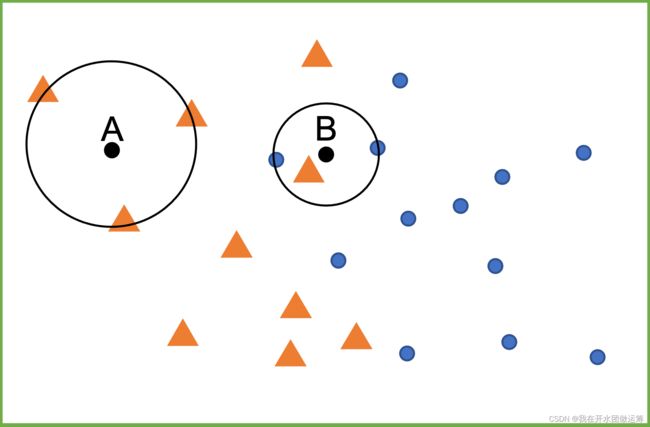
基于K近邻的分类方案很简单：一个查询点被标记的数据标签是由它最近邻点中最具代表性的数据标签来决定的。以下图为例，距离查询点A最近的三个数据的标签均为黄色三角符号，则可以预测A的数据标签也为黄色三角符号；距离查询点B最近的三个数据的标签包括一个黄色三角符号和两个蓝色圆形符号，根据投票中的少数服从多数原则，预测B的数据标签为蓝色圆形符号。

代码实现

以下假定特征数量为2，基于Python代码实现了算法方案中的逻辑。

import numpy as np


def k_neighbors_by_self(x_test, X, y, k):
    # x_test: 测试集特征
    # X: 训练集特征
    # y: 训练集标签
    # k: 近邻数

    x0, y0 = x_test[0], x_test[1]
    
    # 计算每条数据至待预测点的距离平方值
    distance = np.hstack((X, y.reshape(len(y), 1)))
    distance = np.hstack((distance, np.zeros((distance.shape[0], 1))))
    distance[:, 3] = (distance[:, 0] - x0) ** 2 + (distance[:, 1] - y0) ** 2
    sorted_distance = distance[np.lexsort(distance.T)]
    
    # 获取距离待预测点最近的K个数据的标签值，并返回数量最多的那个标签值
    return np.argmax(np.bincount(sorted_distance[0:k, 2].astype(int)))

此外，sklearn包也有K近邻模型

from sklearn import neighbors


def k_neighbors_by_sklearn(x_test, X, y, k):

    # 声明K近邻分类模型
    clf = neighbors.KNeighborsClassifier(k)
    # 训练模型
    clf.fit(X, y)
    
    # 返回模型的预测值
    return clf.predict(np.array(x_test).reshape((1, len(x_test))))

代码测试

为了测试算法方案的可靠性，分两步进行测试：

1. 生成多个离散点，观察k_neighbors_by_self和k_neighbors_by_sklearn返回值是否完全相同。
2. 绘制两个模型的决策边界图形（不同标签值的分界线），观察图形是否完全相同。
   测试集采用学习机器学习算法过程中的常用数据集中”【数据集1】forge：小型模拟分类问题数据集”，即

X, y = forge()

首先看离散点数据。离散点数据设置为：第一维包括7,8,9,10,11共5个数字；x_test中第二维包括-1,0,1,2,3,4,5,共7个数字，组合在一起，x_test中共计35个离散点。以下为离散点测试代码，设置k=3，最终会输出：success_cnt: 35, fail_cnt: 0。即所有离散点的返回值完全相同。

def test_by_points(X, y, k):
    # 模型相同值数量
    success_cnt = 0
    # 模型不同值数值
    fail_cnt = 0
    for x0 in range(7, 12):
        for y0 in range(-1, 6):
            X_test = [x0, y0]
            y_test_by_self = k_neighbors_by_self(X_test, X, y, k)
            y_test_by_sklearn = k_neighbors_by_sklearn(X_test, X, y, k)
            if y_test_by_self == y_test_by_sklearn:
                success_cnt += 1
            else:
                fail_cnt += 1
    print('success_cnt: {}, fail_cnt: {}'.format(success_cnt, fail_cnt))

再看决策边界。以下为测试两个模型的边界绘制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap


def test_by_maps(X, y, k):
    # 提取色谱
    cmap_light = ListedColormap(['orange', 'cyan'])
    cmap_bold = ListedColormap(['darkorange', 'c'])

    # 绘制决策边界。 为此，我们将为网格[x_min，x_max] x [y_min，y_max]中的每个点分配颜色。
    h = .02  # 设置网格中的步长
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    y_test_by_self = np.zeros((xx.shape[0], xx.shape[1]))
    y_test_by_sklearn = np.zeros((xx.shape[0], xx.shape[1]))

    # X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

    for i in range(xx.shape[0]):
        for j in range(xx.shape[1]):
            X_test = [xx[i][j], yy[i][j]]
            y_test_by_self[i][j] = k_neighbors_by_self(X_test, X, y, k)
            y_test_by_sklearn[i][j] = k_neighbors_by_self(X_test, X, y, k)

    # 将结果放入颜色图
    plt.subplot(121)
    plt.pcolormesh(xx, yy, y_test_by_self, cmap=cmap_light)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.axis('equal')
    plt.title('{} neighbors, by {}'.format(k, 'self'))

    plt.subplot(122)
    plt.pcolormesh(xx, yy, y_test_by_sklearn, cmap=cmap_light)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold, edgecolor='k', s=20)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.axis('equal')
    plt.title('{} neighbors, by {}'.format(k, 'sklearn'))

    plt.show()

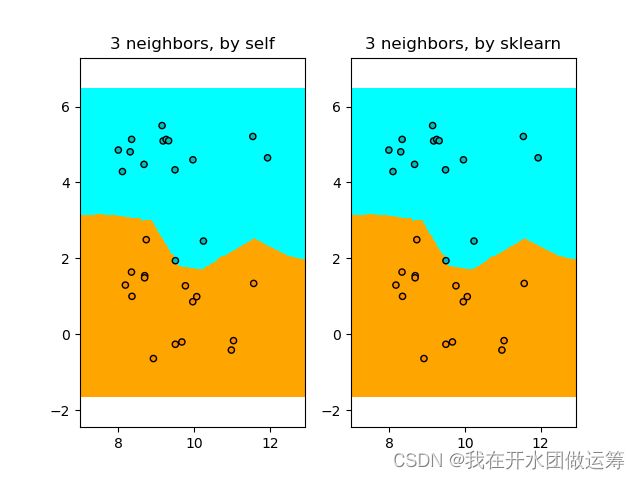
运行以上的代码后，会得到以下的图形。从图上可以看出，两个模型的决策边界也是完全相同的。

通过以上两轮代码测试，可以判定：对K近邻分类算法的理解，是比较准确的。