干货-深度学习37问（读书笔记《深度学习与计算机视觉》）

书籍概况

本书内容有点旧了，但里面的知识仍然给了我一些启发，主要是从几何学和信息论的角度理解深度学习。

干货/深度学习37问

1、在同维度下，仿射变换有些特性可能会发生变化，如长度、面积、角度和距离等，有些量则保持不变，如直线的平行性质、还有线性可分的性质。

2、离散的期望值简单说就是，以概率为加权系数的求和。

3、对伯努利分布的概率而言，当概率为0.5时，熵越大，不确定成都越高

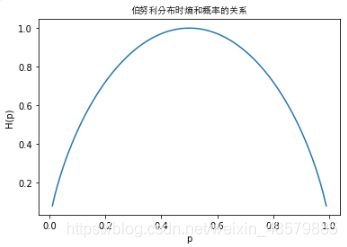
4、最大似然一般采用对数似然函数，不仅将乘法化成了加法，并且求导也因为log函数的性质变得简单。

5、一个白色像素周围的像素通常也会是偏白色的，我们视觉能识别的图像，其实背后隐含的就是一种空间上的相关性。

6、在PCA中，我们说到相关性，指的是统计意义上的相关性，所以适用于PCA的数据也是统计意义上有强相关的数据，而有空间相关性的一些例子可能要用LLE，t-SNE等方法更合适。

7、频率域的乘积类似于空间域的卷积

8、一般的冲量法就像是骑到一个地方，根据当前的坡度，决定车往哪个方向拐，而NAG则是用眼睛看一下前方，判断出坡度，然后根据前方的坡度决定车往哪个方向拐，即是根据预判对当前的路径进行修正。

9、牛顿法的直观解释(高中数学即可)

10、可以把神经网络看作是对一个向量进行分布变换，每一层的输入向量经过这一层的神经元变换之后，相当于一个新的向量，并且新向量的维度等于这一层神经单元的数量，这样一层层变换直到形成最后的输出。

11、在分类问题中，直接度量类别标签不如通过softmax转换成一个分类概率，softmax的作用先通过一次变换让样本对应值都大于0，方便归一化，并且因为exp(x)的特性，让样本的区分度尽量高，然后归一化让多个输出的概率和为1，最后输出的标签就是按照概率比大小了。

12、隐层神经元数量的作用：
可以理解为对空间进行足够精细的非线性扭曲，从分类边界的角度来看，神经元数目对应着用于“拼接”出分类边界的线段数量，神经元越多，越能“拼接”出越复杂的边界。

13、计算图中是不规定计算关系粒度的，计算图是自动求导方法中的一个基础概念，用在深度学习中主要是用来表达输入输出以及中间变量之间的计算关系。

14、当采用sigmoid函数时，梯度消失和爆炸哪个更容易发生？
sigmoid的导数最大为0.25（0附近），而每乘一个梯度，梯度的值又变得更小一些，随着层数的加深，梯度的衰减会非常大，迅速接近0，此为梯度消失；那加入我们把权重初始化为一个较大的值，比如abs(w)>4，此时才可能出现导数和权重相乘大于1的情况。
所以最普遍发生的是梯度消失问题

15、为什么sigmoid这一类函数作为激活函数，随着层数的加深，效果反而会下降？
距离输出层越近的参数，梯度越大，成了主要在进行学习的参数，而远离输出层的参数则只能在接近0的梯度以一个非常小的速率进行，这就是一个恶性循环，因为前面层学习速率慢，参数未必学到了什么特征，所以这些后面层的输入随机性会比较强，这一过程又会让前面层的参数更难学到有效的值。

16、训练过程中出现梯度爆炸会伴随一些细微的信号：
a、模型无法从训练数据中获得更新（如低损失）
b、模型不稳定，导致更新过程中的损失出现显著变化
c、训练过程中，模型损失变成NaN

17、如何解决梯度爆炸？
a、重新设计网络结构，在深度神经网络中，梯度爆炸可以通过重新设计层数更小的网络来解决
b、使用更小的批尺寸对网络训练也有好处，另外也许是学习率的原因，学习率过大导致的问题，减小学习率
c、rnn中，训练过程中在更小的先前时间步上进行更新
d、梯度剪裁、正则
梯度裁剪的思想是设置一个阈值，更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内，比如

e、lstm是不那么容易发生梯度消失的，主要原因在于其内部的“门”，通过“门”可以在更新的时候，“记住”前几次训练的“残留记忆”
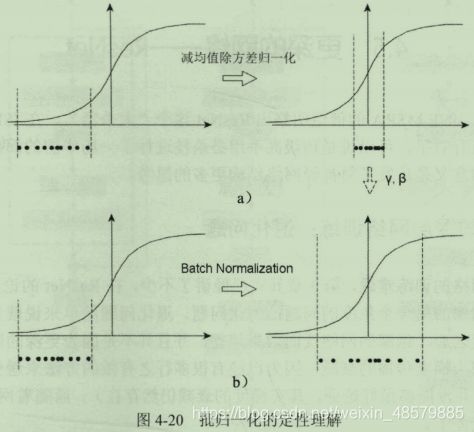
f、Batchnorm是深度学习发展以来提出的最重要的成果之一，具有加速网络收敛、提升训练稳定性的效果，其本质是解决反向传播中的梯度问题，即批规范化，通过规范化操作将输出信号规范化到均值为0、方差为1。

18、梯度消失：
梯度消失：一是在深层网络中；二是采用了不合适的损失函数，比如sigmoid（导数最大为0.25，神经网络的反向传播是逐层对函数偏导相乘，因此当神经网络层数非常深的时候，最后一层产生的偏差就因为乘了很多的小于1的数而越来越小，最终就会变为0，从而导致层数比较浅的权重没有更新，这就是梯度消失。

19、任何一个神经网络都是多次前向后向计算的过程

20、为什么relu会好？
抛开我们比较熟知的公式层面的解释，从神经科学的角度来看，神经元的激活率是非常低的，而这刚好符合relu的性质，信息只能在relu的输入大于0的区域进行传播，带来的另外一个优点就是稀疏性，稀疏性不仅对网络的性能提高有帮助，也符合神经学，是一种仿生的模拟。

21、如何从信息论的角度看待后向传播
无论是梯度消失还是爆炸，其根源都是链式求导法则的连续相乘带来的不稳定性，从这个角度看，梯度消失和爆炸其实是一个问题，就是梯度累计相乘带来的不稳定性。那么，是否解决了梯度消失和爆炸，深层网络的训练解决了呢？不然，因为消失和爆炸只是梯度传播过程中不稳定性体现的两个方面，其它一些因素也影响了深层网络的训练，比如

除了从信息论的角度，梯度计算本身的性质也会导致信息随层数的增加而丢失

22、小批量随机梯度下降(mini-batch)具有一定的随机性，但在深度学习应用中是一种优点，因为深度学习中面临的基本都是非凸优化问题。

23、深度学习的凸与非凸
凸：顺着梯度方向走到底，一定是最优解
大部分传统机器学习问题都是凸的
非凸：顺着梯度方向走到底只能保证是局部最优、不能保证是全局最优
深度学习以及小部分传统机器学习问题都是非凸的

24、如何直观理解数据增加
在机器学习中，数据通常都是来源于一个分布，比如猫的图片，无论图片中的猫是什么颜色、什么姿势、眼睛是瞪着还是眯着，都能看出是一只猫。而所有猫的图片，都可以看作是来自于一个分布。
所以在做数据平衡的时候可以考虑模拟这个分布来产生一些和已有数据不完全一样的数据，那具体到猫的例子，就是可以考虑把图像旋转一个角度，左右镜像对称，明暗度做一些改变，或者裁剪等。

25、训练数据和测试数据来源于同一个分布，是机器学习中一个基本假设，白话一点就是根据体温、心率和血压来判断一个人是否平静，无论这个模型判断人有多准确，都难以直接用到一只猫身上。

26、参数模型可以理解为参数数量给定的模型，比如神经网络，定好了结构的话，参数数量是确定不变的，学习过程只要根据训练数据和损失函数优化参数的值就可以了，因为参数和形式确定，所以给定一个参数模型，模型的能力也是确定的。
27、奥卡姆的意义是指，只有针对特定问题，特定的数据分布时，找到一个好的算法才有意义。

28、从几何学的角度深入浅出理解数值稳定性

29、需要算法与环境交互获得数据是强化学习。

30、常常有人拿强化学习和监督学习进行比较，的确，强化学习的特性在某种程度上相当于从环境中获得了对数据的标注，但这两种类型的算法还是有很大不同的，首先，强化学习的目标和监督学习不一样，强化学习看重的是行为序列下的长期收益，而监督学习往往关注的是和标签或已知输出的误差，强化学习的奖惩概念是没有正确或错误之分的，而监督学习标签就是正确的，强化学习是一个学习+决策的过程，并且有和环境交互的能力，这都是监督学习不具备的。

31、对于多通道的输入，处理非常简单，就是给每个通道用不同的卷积核做卷积，然后结果加一块就可以了。

32、池化大概是卷积和普通网络最不同的地方，**池化这个概念本身并不是一个具体的操作，而是代表着一种对统计信息的提取。**在实际的网络中，池化的stride常常要小于池化区域的边长，这样能使相邻池化区域有一定的重叠。

33、直观形象的理解深度学习中的分层表达

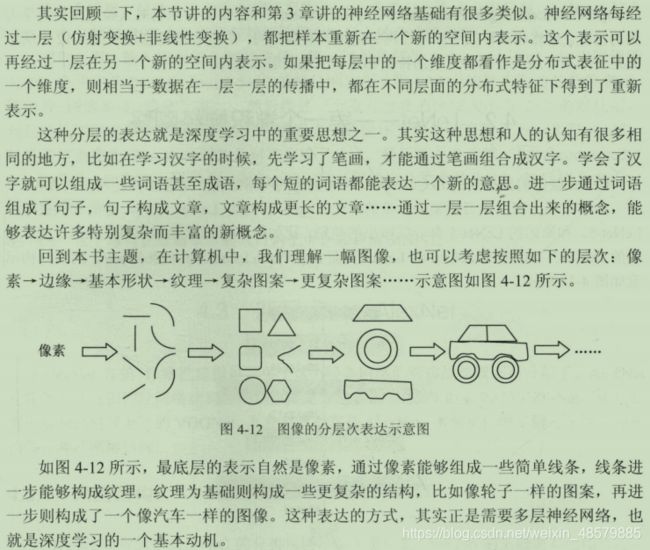
34、像GoogleNet等网络出现了好几个loss单元，这样做的目的是为了帮助网络的收敛，有些辅助loss的计算被乘以系数0.3，然后和最后的loss相加作为最终的损失函数来训练网络。

35、从几何的角度直观的理解批归一化的作用（为什么批归一化的本质是解决梯度问题）


36、以ResNet为例解释网络的退化问题
退化问题简单来说就是，随着层数加深到一定程度之后，越深的网络反而效果越差，并且不是因为更深的网络造成了过拟合，也未必是因为梯度传播的衰减，因为已经有很多方法来避免这个问题了。

关于resnet，也可以从集成的角度看待。

37、残差指的是预测值和观测值之间的差异，而误差指的是观测值和真实值的差异。

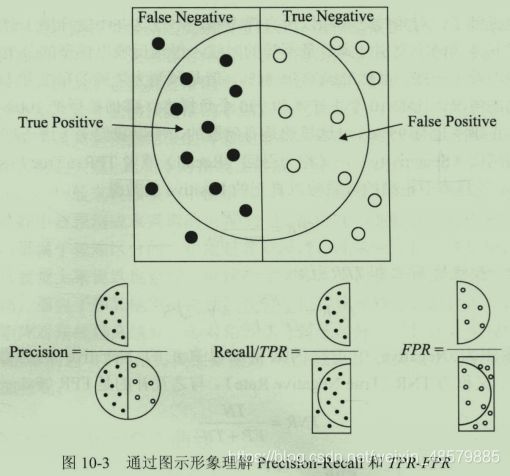
38、书中280页有一个比较形象的解释TP的图

39、计算马氏距离等效于在变换后的空间里计算欧氏距离

引用

熵：https://www.cnblogs.com/xiaoyuanqujing/articles/11657263.html
频域：https://zhuanlan.zhihu.com/p/87905695
github参考地址：https://github.com/frombeijingwithlove/dlcv_for_beginners