【蓝桥杯】带你走进动态规划的世界（一）

写在前面

由于蓝桥杯对DP问题的考察加大，那么DP问题也就成了我们备考蓝桥杯的重点内容。我打算分三次写完DP，第一篇呢是为了让小伙伴们初步理解DP思想，里面的例题是非常经典同时又是非常基础的。
蓝桥杯的比赛时间越来越近了，所以最近我会加快备考文章的更新，小伙伴们不要着急噢~考前一定会将常考的知识点更新完的。
好啦废话不多说，进入我们今天的DP学习吧~

---

一、入门——从记忆化搜索说起

在前面的文章中我们已经对动态规划做了铺垫，不知道小伙伴们还记不记得在讲解搜索算法时我也给大家讲了记忆化搜索，还说记忆化搜索是学习DP思想的基础。有些小伙伴没看过之前的文章，因此呢这篇文章还是要从记忆化搜索说起。

以斐波那契数列为例，它的第一项为1，第二项为1，从第三项开始，每一项的值都是前面两项的和。让我们求第n项的是多少。对于这个问题，我们从最开始的递归思想来看。

int fib(int n)
{
	if (n == 1 || n == 2) return 1;
	return fib(n - 1) + fib(n - 2);
}

这个递归的时间复杂度是O(2^n)，随着n的增大，呈指数级别增长。递归的时间复杂度之所以高，是因为它涉及了很多重复性计算。比如在计算fib(5)的时候，fib(5) = fib(4) + fib(3)。接下来计算fib(4)，fib(4) = fib(3) + fib(2)。fib(4)计算完后就会再计算fib(3)。然而我们之前在计算fib(4)的时候已经算出fib(3)了。fib(3)被重复计算了两次。当n很大的时候。重复计算的工作就越来越多。

为了避免重复计算，我们可以在计算的过程中将已经计算过的值保存下来，等到再一次遇到的时候就可以直接使用。开一个dp[]数组，dp[i]存储fib(i)的值。dp[i] = 0表示还没有计算过。

int dp[20];
int fib(int n)
{
	if (n == 1 || n == 2) return 1;
	if (dp[n]) return dp[n];//计算过，直接返回dp[n]
	return dp[n] = fib(n - 1) + fib (n - 2);
}

说一下比较官方的东西，将每个求解过的子问题的解记录下来，当下一次遇到同样的子问题时，就可以直接使用之前记录的结果，而不用重复计算。这就是记忆化搜索的精髓。

下面我画两张图来让小伙伴们看看递归和使用记忆化搜索优化后的递归的搜索过程。

使用记忆化搜索后的时间复杂度为O(n)，将指数级别的复杂度降到了线性级别。

在下面对DP的讲解中，小伙伴们也会同样看到，DP会记录重复问题的解，下次再碰到时就会直接使用之前记录的问题的解。

---

二、开端——什么是DP思想

说明：以下对DP思想的讲解比较官方，不想看的小伙伴可以直接跳到第三大内容，DP的分析方法。

DP思想也就是动态规划思想，Dynamic programming，简称DP。

我们以一个数塔问题为例，给大家讲解以下到底什么是DP，什么情况下可以用DP等一些主要的问题。

将一些数字排成数塔的形状，其中第一层有一个数字，第二层有两个数字，第n层有第n个数字。现在要从第一层走到第n层，每次只能走向下一层连接的两个数字中的一个，问最后将路径上的所有数字相加后得到的和最大是多少？

我们可以尝试用DFS来解决这个问题，dfs维护已经选择完第index层，选择的数字是(index,y)，已经选择的数字之和sum。当处理完最后一层时用一个变量ans来更新数字之和的最大值。由于每个数字都有两个分支，因此

• 当前已经选择完第index层，选择的数为(index, y)
• 当前已经选择完第index层，选择的数为(index, y + 1)

穷举所有可能的时间复杂度是$O(2^n)$。

#include 
using namespace std;

const int N = 10;
int f[N][N];
int ans;
int n;

void dfs(int index, int y, int sum)
{
    if (index == n)
    {
        ans = max(ans, sum);
        return;
    }
    dfs(index + 1, y, sum + f[index + 1][y]);
    dfs(index + 1, y + 1, sum + f[index + 1][y + 1]);

}

int main()
{  
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)//数塔只需要输入j <= i的部分
        {
            cin >> f[i][j];
        }
    }
    dfs(0, 0, f[0][0]);//这句代码意思是已经选择完第0层，选的是(0,0)，当前的sum是f[0][0]。
    // dfs(0, 0, 0);error
    cout << ans << endl;
    return 0;
}

我们来看看如何优化这个时间复杂度呢？从5开始出发，沿5->8->7的路线到达7,之后就是枚举从7出发到达最底层的所有路径。而我们沿5->3->7同样可以到达7，又会枚举从7出发到达最底层的所有路径。这样从7出发到达最底层的路径就被重复访问了。越靠近底层的数字被重复访问的次数就越多。我们可以在第一次访问到7的时候就将其到达最底层的所有路径中的最大和记录下来，再一次从7出发时就可以直接利用之前记录的结果了。小伙伴是不是发现这种思想不就是前面讲的记忆化搜索嘛。

设dp[i][j]表示从第i行出发第j个数字出发，到达最底层的所有路径中的最大数字之和。假设我们要求dp[0][0]，而它的值由dp[1][0]和dp[1][1]中最大的那个来决定。即dp[0][0] = max(dp[1][0], dp[1][1]) + f[0][0]。进而我们可以写出dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + f[i][j]。

dp[i][j]被称作状态，这里的递推式就叫做状态转移方程。直接可以得出结果的状态叫做边界。最后一行的状态就是数字本身。即dp[n - 1][j] = f[n - 1][j]。

#include 
using namespace std;

const int N = 10;
int f[N][N];
int dp[N][N];
int n;

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
        {
            cin >> f[i][j];
        }
    }
    for (int i = 0; i < n; i++)//处理边界
    {
        dp[n - 1][i] = f[n - 1][i];
    }
    for (int i = n - 2; i >= 0; i--)//遍历DP数组并赋值，要从后往前枚举i，因为某个状态是由下一行的状态决定的。
    {
        for (int j = 0; j <= i; j++)
        {
            dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + f[i][j];
        }
    }
    cout << dp[0][0] << endl;
    return 0;
}

从斐波那契数列那道题中，我们可以看出只有问题含有重叠子问题时，才可以使用记忆化搜索，将重叠子问题的结果记录下来，再碰到该问题时就直接使用。比如求fib(5)先求fib(4)，fib(4)需要先求fib(3)，将fib(3)结果记录下来。下次碰到fib(3)就不用继续递归了，直接使用之前记录的结果即可。

从数塔问题中引申出一个概念，最优子结构。简单来说一个问题的最优解可以由其子问题的最优解有效的构造出来，那么我们就称该问题具有最优子结构。dp[0][0]是由其两个子问题dp[1][0]和dp[1][1]中的最大值决定的。因此数塔问题具有最优子结构。

我们再来讨论一个概念，状态的无后效性。在这里贴一个算法笔记中对无后效性的解释。

嗯我知道有很多小伙伴看不懂说的是什么， 简单来说就是过去的状态只能通过当前的状态来影响未来的状态。比如还是以数塔问题为例，当前状态为dp[1][0],它过去的状态dp[2][0]和dp[2][1]只能通过该状态去影响dp[0][0]的值，而不能直接去影响dp[0][0]的值。dp[1][1]也是同样的道理。简单来说就是dp[0][0]是由dp[1][0]和dp[1][1]决定的，与其他状态无关。

我们所定义的状态必须具有无后效性，否则以它为基础的状态转移方程是无法得到正确结果的。动态规划的核心就是设计状态和状态转移方程，这也是DP问题的难点所在。

三、切入——DP的分析方法

下面将介绍两种方法来分析下DP问题的一般做法。 一种是Carl大神的动规五部曲，另一种是ACwing中yxc的闫氏DP分析法，也叫从集合角度去分析DP问题。
Carl博客地址
另外推荐小伙伴们去ACwing这个网站，相信你可以找到很多干货。

One Method 动规五部曲

由于该方法不是本文的讲解重点噢~想更深入了解动规五部曲，小伙伴们可移步到Carl大佬的博客去看，也可关注微信公众号代码随想录。真心推荐！

Another Method 从集合角度去分析DP问题

下面将通过三道经典的例题来讲解如何用集合方法来分析DP问题。

四、分析——DP三大模型

1. 组合模型——01背包问题

题目链接

背包系列的问题相必很多小伙伴都知道，而01背包问题又是背包系列的基础，也是初学者入门DP的一道坎。我们之前在讲搜索算法的时候将01背包问题用DFS实现了一遍，它的时间复杂度很高，今天我们用DP来重新做一下这道题。

题目分析
先用集合分析的方法解决这道题。
令w[i]表示每个物品的体积，令v[i]表示每个物品的价值。

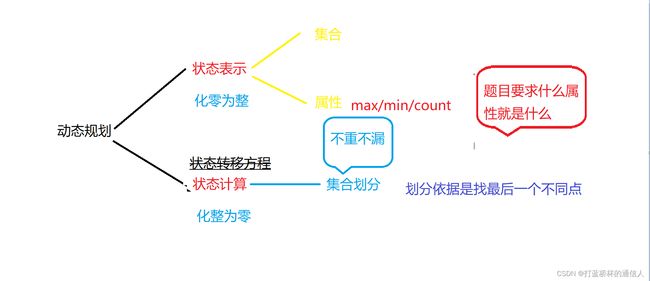
• 状态表示 dp[i][j]
  • 集合：从前i个物品中选，总体积不超过j的所有方案
  • 属性：max
• 状态计算——集合划分
  • 找最后一个不同点。该集合的最后一个不同点就是第i个物品到底选不选。
  • 不选第i个物品，从前i个物品中选，总体积不超过j，而且不选第i个物品，等价于从前i-1个物品中选，总体积不超过j。即dp[i][j] = dp[i - 1][j] 。
  • 选第i个物品，那么该集合就变成从前i-1个物品中选，总体积不超过j-w[i] 的所有方案。dp[i][j] = dp[i - 1][j - w[i]] + v[i]。
  • 取最大值即可。dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]

是不是觉得这样分析变得非常简单了。好啦我们的状态和状态转移方程都写出来了，再来看一下边界问题吧。前0个物品也就是没有物品时，不管j是多少，总价值总是0，另外j为0时，不管i是多少，总价值也是0。（这是很显然的）

• dp[0][j] = 0
• dp[i][0] = 0

当然这两行代码我们可写可不写，因为dp数组我们开始的时候就将它初始化成0，这样就不用额外处理边界了。

AC代码

//DP解法
//01背包问题
#include 
using namespace std;

const int N = 10010;
int n, V;
int w[N], v[N];//w[i]表示重量，v[i]表示价值
int dp[N][N];

int main()
{
    cin >> n >> V;
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i] >> v[i];
    }

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {	//当前选择的物品体积超过了背包容量j，那么我们就不能选这个物品.
            if (j < w[i])
            {
                dp[i][j] = dp[i - 1][j];
            }
            else
            {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
            }
        }
    }
    cout << dp[n][V] << endl;
    return 0;    
}

另外我们对01背包问题的代码进行优化，时间复杂度为$O(nv)$，不能再进行优化了，但是空间复杂度还可以继续优化。
利用滚动数组，将dp[i][j]转变成一维的dp[j]。

滚动数组优化 空间复杂度$O(V)$

我们在来看看01背包的一维写法，这是基于滚动数组的思想。既然第i个状态完全取决于第i-1个状态，求第i+1个状态又完全用不到第i-1个状态，那么我们可以用一个一维数组dp[],省略第一维，降低空间复杂度。那么仿照二维的dp递推式，我们可以写出一维递推式：

• dp[j] = max(dp[j], dp[j - w[i]] + v[i])，当j >= w[i]时
• dp[j] = dp[j]，当j < w[i]时

可以看出当j < w[i]时，dp状态没有发生改变，那么我们可以确定j的枚举范围是w[i] <= j <= W。

确定枚举范围后，再考虑下枚举的顺序，是从前往后枚举，还是从后往前枚举呢？假设从前往后枚举，那么在计算i状态时的dp[j]时，dp[j - w[i]]不是i-1时的状态了，而是i时的状态了，它被污染了(dp[j - w[i]要比dp[j]先算出来)，因此我们只能从后往前枚举j，这样计算dp[j]的时候用到的状态都是i-1时的状态了。

//滚动数组优化
//01背包问题
#include 
using namespace std;

const int N = 10010;
int n, V;
int w[N], v[N];//w[i]表示重量，v[i]表示价值
int dp[N];

int main()
{
    cin >> n >> V;
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i] >> v[i];
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = V; j >= w[i]; j--)//j只能从后往前遍历
        {
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
        }
    }
    cout << dp[V] << endl;
    return 0;
}

小伙伴们可以思考一下是否可以颠倒i和j的顺序呢，让i在内层，j在外层。先遍历背包体积，再遍历物品。
答案是不可以的，这样就会导致dp[j]只能放入一个物品，dp[V]的值永远是最后一个物品的价值。

---

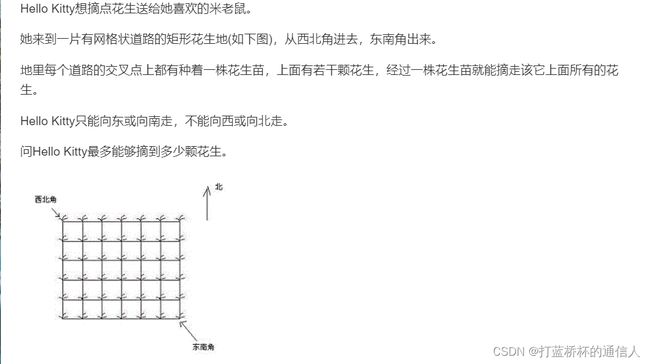
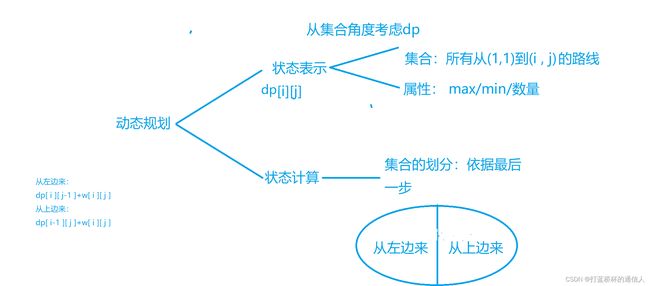
2. 路线模型——摘花生

题目链接



题目分析

简单分析：

• dp[i][j]表示从(1,1)到(i,j)所有路径中能摘得花生最多的路径。
• 集合划分的依据是最后一个不同，也就是到达(i,j)是从左边来的，还是从上边来的。
• 集合要满足不重复(对于求数量而言)，不漏(对于求max,min,ans而言)

AC代码

#include 
using namespace std;
//dp[i][j] = max(dp[i - 1][j] + a[i][j], dp[i][j - 1] + a[i][j])
const int N = 110;
int T;
int dp[N][N];
int n, m;
int a[N][N];

int main()
{
    cin >> T;
    while(T--)
    {
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                cin >> a[i][j];
            }
        } 

        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= m; j++)
            {
                dp[i][j] = max(dp[i - 1][j] + a[i][j], dp[i][j - 1] + a[i][j]);
            }
        }
        cout << dp[n][m] << endl;
    }   
}

---

3. 线性模型——最长上升子序列

题目链接

题目分析

子序列不一定要连续。

在这里简单说一下集合划分那一步，找最后一个不同点，对于这个问题来说就是以i结尾的子序列的倒数第二个数。它可以是第1到第i-1中的任何一个，当然必须满足a[i]>a[j]。也可以没有倒数第二个数，它本身就是个严格单调递增的子序列。那么我们要在开始的时候就将dp数组初始化成1。集合划分的依据理解以后，思路就特别清晰了。对某个特定的i，我们可以从第一个数开始枚举，直到i-1个数，判断a[j]是否满足小于a[i]的条件，不断更新dp[i]的值。dp[i] = max(dp[i], dp[j] + 1)。

AC代码

#include 
#include 
using namespace std;

const int N = 1010;
int n;
int dp[N];//dp[i] = dp(K) + 1
int a[N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    for (int i = 1; i <= n; i++)//初始化DP数组
    {
        dp[i] = 1;
    }
    for (int i = 2; i <= n; i++)
    {
        for (int j = 1; j < i; j++)
        {
            if (a[j] < a[i])//满足严格单调递增条件
            {
                dp[i] = max(dp[i], dp[j] + 1);
           }
        }
    }
    // cout << dp[n] << endl;
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        //cout << dp[i] << endl;
        ans = max(ans, dp[i]);
    }
    cout << ans << endl;
}

DP数组的打印
在做DP问题的时候，写代码之前一定要将状态转移在DP数组中的具体情况模拟一遍，做到心中有数。确定最后推导出来的结果就是自己想要的答案。然后编写代码，如果没有AC，就打印出DP数组，看看结果和自己想的哪里不一样。
学会调试代码也是一种很重要的能力。

---

写在后面

这篇文章跟小伙伴们讲解了DP思想到底是什么，如何用集合方法去分析DP问题。
下一篇文章会继续对DP问题进行更深入的探讨，小伙伴们可以期待一下噢~
觉得这篇文章写的不错的话，一键三连支持一下吧，蟹蟹~